K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
8 tháng 11 2021
a/ Ta có: \(\begin{matrix}a\text{ // }b\\a\perp AB\end{matrix}\Rightarrow b\perp AB\)
b/ \(\hat{ACD}+\hat{CDB}=180^o\) (trong cùng phía, a // b)
\(\Rightarrow\hat{CDB}=180^o-\hat{ACD}=60^o\)
\(\hat{ACD}+\hat{aCD}=180^o\) (kề bù)
\(\Rightarrow\hat{aCD}=180^o-\hat{ACD}=60^o\)
HM
2
15 tháng 9 2021
\(\dfrac{2}{5}-\left|\dfrac{1}{2}-x\right|=6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6\)
\(\Leftrightarrow\left|\dfrac{1}{2}-x\right|=-\dfrac{28}{5}\)( vô lý do \(\left|\dfrac{1}{2}-x\right|\ge0\forall x\))
Vậy \(x\in\left\{\varnothing\right\}\)
15 tháng 9 2021
\(\Rightarrow\left|\dfrac{1}{2}-x\right|=\dfrac{2}{5}-6=-\dfrac{28}{5}\\ \Rightarrow\left[{}\begin{matrix}\dfrac{1}{2}-x=-\dfrac{28}{5},\forall\dfrac{1}{2}-x\ge0\\\dfrac{1}{2}-x=\dfrac{28}{5},\forall\dfrac{1}{2}-x< 0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{61}{10},\forall x\le\dfrac{1}{2}\left(loại\right)\\x=-\dfrac{51}{10},\forall x>\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\Rightarrow x\in\varnothing\)
20 tháng 4 2016
xét ở tử số ta có:
-1;2;-6;24;........
Ta sẽ được -1*-2=2;2*-3=-6;-6*-4=24
Suy ra:số hạng thứ 5 của dãy là:
(24*-5)/a^6=-120/a^6
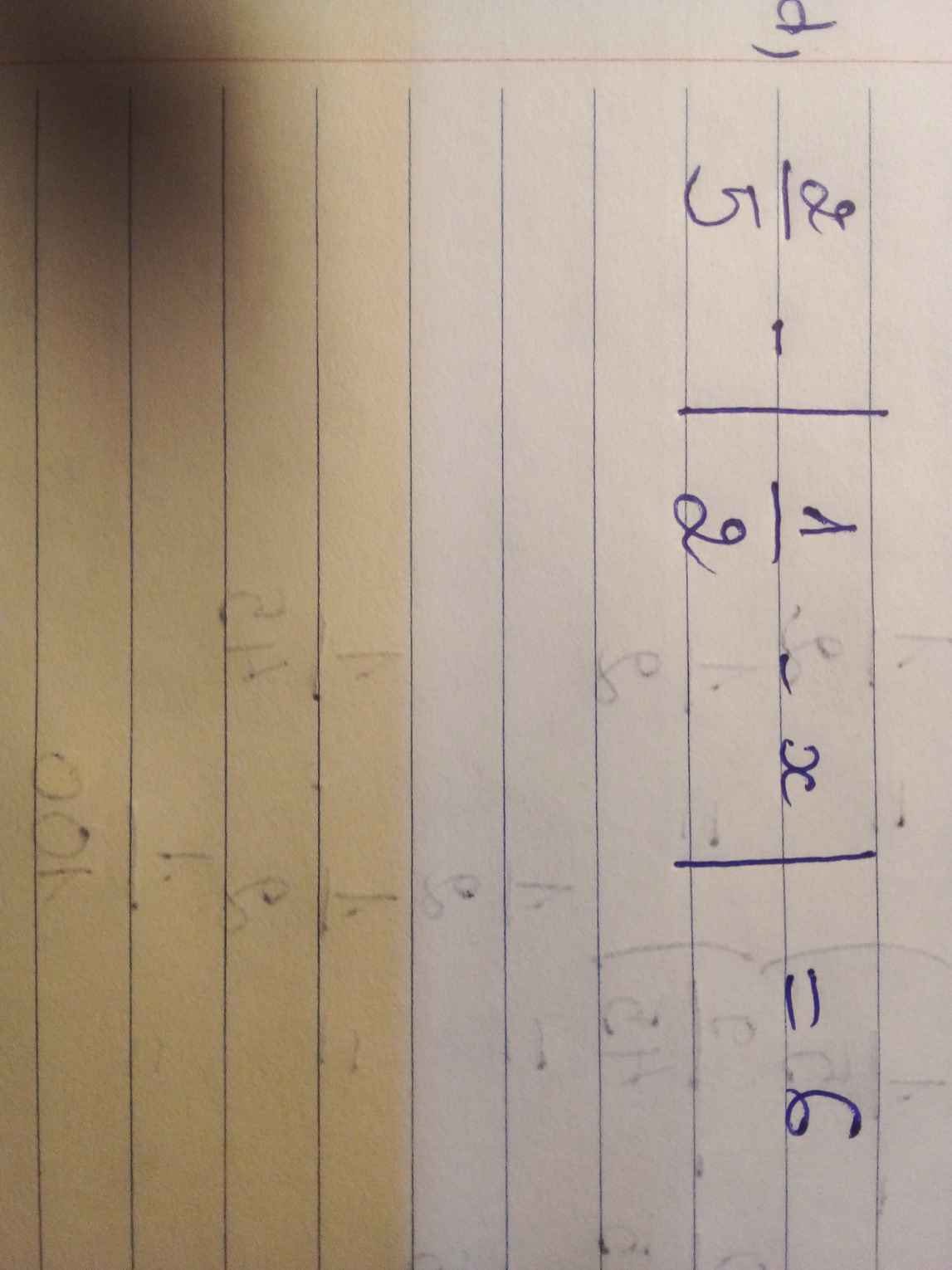
Làm ngay bây giờ cho mk vs, mk cần gấp lắm
TT
0
Lời giải:
Đặt $\frac{x+1}{3}=\frac{y-2}{4}=\frac{z-1}{13}=a$
$\Rightarrow x+1=3a; y-2=4a; z-1=13a$
$\Rightarrow x=3a-1; y=4a+2; z=13a+1$
Thay vào điều kiện $2x-3y+z=35$ thì:
$2(3a-1)-3(4a+2)+(13a+1)=35$
$\Rightarrow 7a-7=35$
$\Rightarrow a=6$
$\Rightarrow x=3.6-1=17; y=4.6+2=26; z=13.6+1=79$
Đáp án 1.