
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C


\(A^2=8+2\sqrt{16-10-2\sqrt{5}}\\ A^2=8+2\sqrt{6-2\sqrt{5}}\\ A^2=8+2\left(\sqrt{5}-1\right)=6+2\sqrt{5}\\ A=\sqrt{6+2\sqrt{5}}=\sqrt{5}+1\)
Đặt \(\sqrt{10+2\sqrt5}\)= a. Ta có A = \(\sqrt{4+a}+\sqrt{4-a}\)
=> A2 = 4 + a + 4 - a + 2\(\sqrt{(4+a)(4-a)}\)
=> A2 = 8 + 2\(\sqrt{16-a^2}\)
=> A2 = 8 + 2\(\sqrt{16 - 10 + 2\sqrt5}\)
=> A2 = 8 + 2\(\sqrt{5+2\sqrt{5}+1}\)
=> A2 = 8 + 2\(\sqrt{(\sqrt{5}+1)^2}\)
=> A2 = 8 + 2\(\sqrt5\) + 2
=> A = \(\sqrt{2\sqrt{5}+10}\)

a) \(\Rightarrow A=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(\Rightarrow A=\sqrt{x}-1+\sqrt{x}\)
\(\Rightarrow A=2\sqrt{x}-1\)
b) \(\Rightarrow A=2.4-1=7\)
a) \(A=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}=\sqrt{x}-1+\sqrt{x}=2\sqrt{x}-1\)
b) \(A=2\sqrt{x}-1=2\sqrt{16}-1=2.4-1=7\)

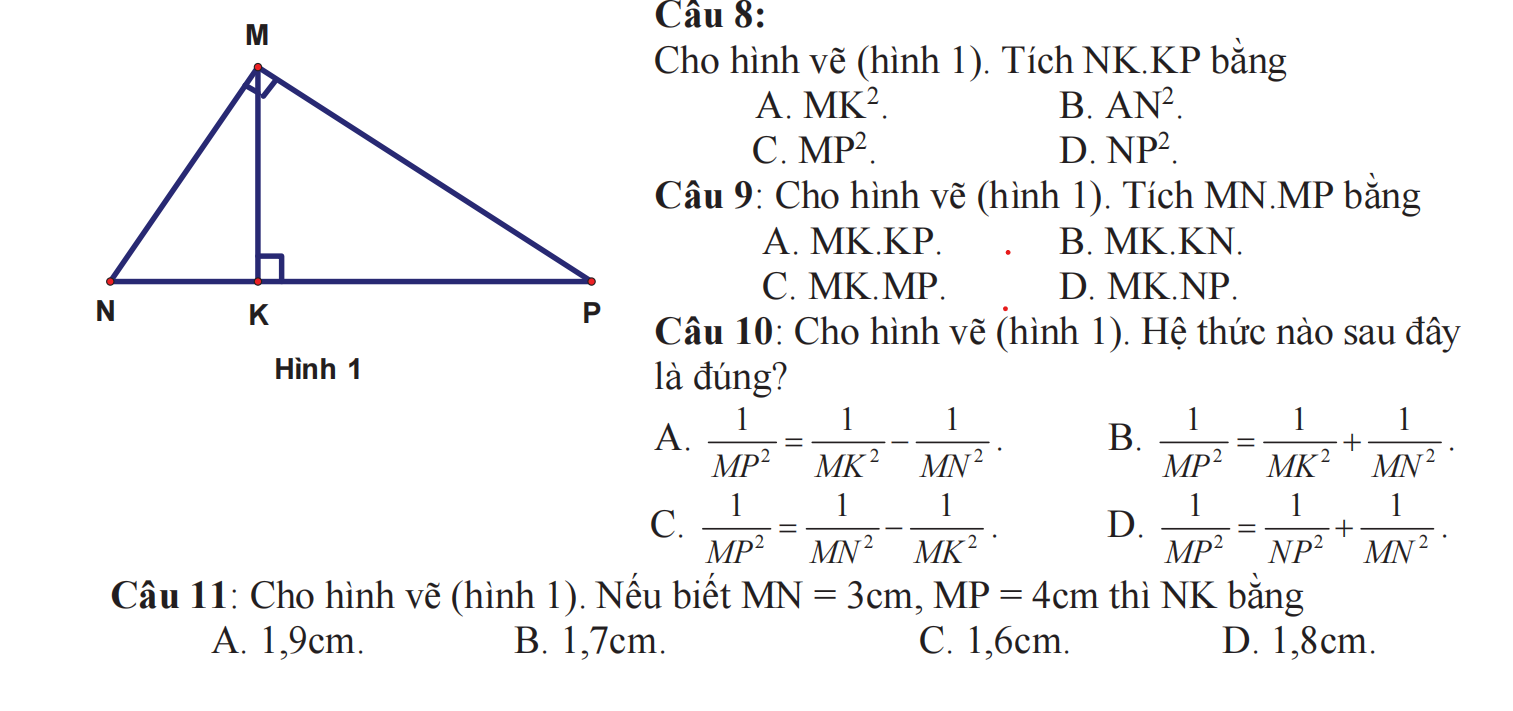
8A 9D 10 Hệ thức đúng: \(\dfrac{1}{MK^2}=\dfrac{1}{MN^2}+\dfrac{1}{MP^2}\)(k thấy trong các câu chọn)
11D


Ta có: \(AB^2+HC^2=\left(AA'^2+A'B^2\right)+\left(A'H^2+A'C^2\right)\)
\(=\left(AA'^2+A'C^2\right)+\left(A'B^2+A'H^2\right)=AC^2+HB^2\)
Lại có: \(BC^2+HA^2=\left(BB'^2+B'C^2\right)+\left(B'H^2+B'A^2\right)\)
\(=\left(BB'^2+B'A^2\right)+\left(B'C^2+B'H^2\right)=AB^2+HC^2\)
\(\Rightarrow AB^2+HC^2=AC^2+HB^2=BC^2+HA^2\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)




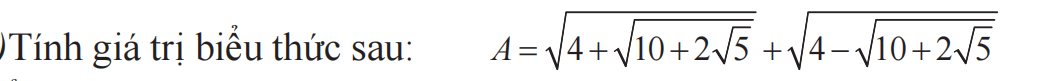
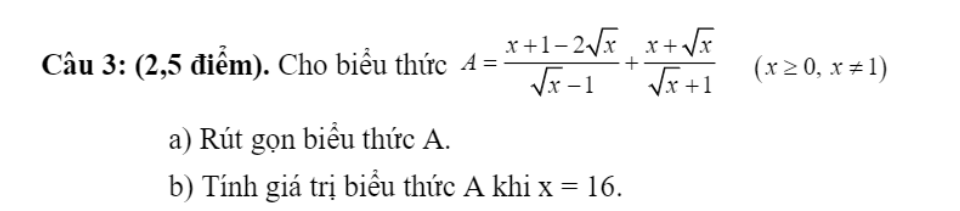


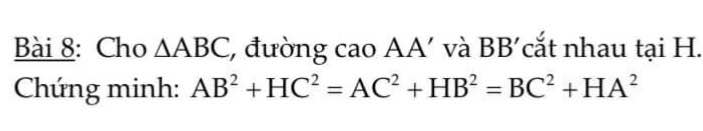
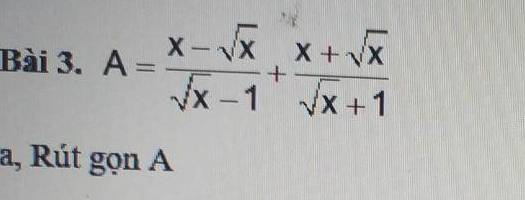
X= 16