
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\dfrac{3x-6+5x+10+3x-26}{\left(x-2\right)\left(x+2\right)}=\dfrac{11x-22}{\left(x-2\right)\left(x+2\right)}=\dfrac{11}{x+2}\)

Câu 1:
a)2x-3=5
\(\leftrightarrow\)2x=5+3
\(\leftrightarrow\)2x=8
\(\leftrightarrow\)x=4
Vậy pt có tập nghiệm S={4}
b)(2x+1)(x-3)=0
\(\leftrightarrow\) 2x+1=0
Hoặc x-3=0
\(\leftrightarrow\)x=-1/2
x=3
Vậy pt có tập nghiệm S={-1/2;3}
d)3x-4=11
\(\leftrightarrow\)3x=11+4
\(\leftrightarrow\)3x=15
\(\leftrightarrow\)x=5
Vậy pt có tập nghiệm S={5}
e)(2x-3)(x+2)=0
\(\leftrightarrow\)2x-3=0
Hoặc x+2=0
\(\leftrightarrow\)x=3/2
hoặc x=-2
Vậy pt có tập nghiệm S={3/2;-2}
Câu 2:
a)2x-3<15
\(\leftrightarrow\)2x<15+3
\(\leftrightarrow\)2x<18
\(\leftrightarrow\)x<9
Vật bpt có tập nghiệm S={x|x<9}
c)5x-2<18
\(\leftrightarrow\)5x<20
\(\leftrightarrow\)x<4
Vậy bpt có tập nghiệm S={x|x<4}
Mấy bài phân số nhác gõ quá~

80cm=0,8m, 60cm=0,6m
Diện tích xung quanh căn phòng là:
\(2\left(10+5\right).4=120\left(m^2\right)\)
Diện tích cửa chính:
\(1,8\times2=3,6\left(m^2\right)\)
Diện tích 2 cửa sổ:
\(0,8\times0,6\times2=0,96\left(m^2\right)\)
Diện tích cần sơn:
\(200-\left(3,6+0,96\right)=115,44\left(m^2\right)\)
Chi phí tiền công:
\(195,44\times25000=2886000\) đồng

Bài 5:
a: 2x-(3-5x)=4(x+3)
=>2x-3+5x=4x+12
=>7x-3=4x+12
=>3x=15
=>x=5
b: =>5/3x-2/3+x=1+5/2-3/2x
=>25/6x=25/6
=>x=1
c: 3x-2=2x-3
=>3x-2x=-3+2
=>x=-1
d: =>2u+27=4u+27
=>u=0
e: =>5-x+6=12-8x
=>-x+11=12-8x
=>7x=1
=>x=1/7
f: =>-90+12x=-45+6x
=>12x-90=6x-45
=>6x-45=0
=>x=9/2

b: ĐKXĐ: x>=2/3
PT=>(x-1)(x-2)+(x-1)*căn 3x-2=0
=>căn 3x-2+x-2=0
=>căn 3x-2=-x+2
=>x<=2 và 3x-2=x^2-4x+4
=>x^2-4x+4-3x+2=0 và x<=2
=>x=1
c: =>x+3+x-4-2căn (x^2-x-12)=1
=>2*căn x^2-x-12=2x-1-1=2x-2
=>căn x^2-x-12=x-1
=>x>=1 và x^2-x-12=x^2-2x+1
=>x=13

a: Xét tứ giác AECF có
AE//CF(AB//CD)
AE=CF
Do đó: AECF là hình bình hành
b: AE+EB=AB
CF+FD=CD
mà AE=CF và AB=CD
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
=>DE=BF
c:
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔAIC có
D,O lần lượt là trung điểm của AI,AC
=>DO là đường trung bình
=>DO//CI
d: AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>AC,EF,BD đồng quy(do cùng đi qua O)

a, Xét tứ giác ADHE có ^ADH = ^AEH = ^DAE = 900
=> tứ giác ADHE là hcn
=> AH = DE (2 đường chéo bằng nhau)
b, Xét tam giác AHB và tam giác CHA ta có
^AHB = ^CHA = 900
^HAB = ^HCA ( cùng phụ ^HAC )
Vậy tam giác AHB~ tam giác CHA (g.g)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH^2=BH.CH\)
c, Xét tam giác AHD và tam giác ABH có
^ADH = ^AHB = 900
^A _ chung
Vậy tam giác AHD ~ tam giác ABH (g.g)
\(\dfrac{AH}{AB}=\dfrac{AD}{AH}\Rightarrow AH^2=AD.AB\)(1)
tương tự tam giác AEH ~ tam giác AHC (g.g)
\(\dfrac{AE}{AH}=\dfrac{AH}{AC}\Rightarrow AH^2=AE.AC\left(2\right)\)
Từ (1) ; (2) suy ra \(AD.AB=AE.AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét tam giác ADE và tam giác ACB
^A _ chung
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\left(cmt\right)\)
Vậy tam giác ADE ~ tam giác ACB (c.g.c)

\(\dfrac{x+2}{x-3}< 0\)vì \(x+2>x-3\)
\(\left\{{}\begin{matrix}x+2>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x< 3\end{matrix}\right.\)<=> -2 < x < 3

\(3\left(x-1\right)^2-3x\left(2-5\right)=21\)
\(\Leftrightarrow3x^2-6x+3+9x-21=0\)
\(\Leftrightarrow3x^2+3x-18=0\)
\(\Leftrightarrow3\left(x^2+x-6\right)=0\)
\(\Leftrightarrow3\left(x-2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=-3\end{cases}}\)
Vậy \(S=\left\{2;-3\right\}\)
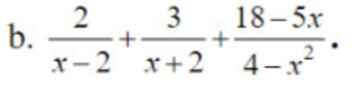 Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn
Giải giúp mình với,chi tiết hết luôn ạ,xin cảm ơn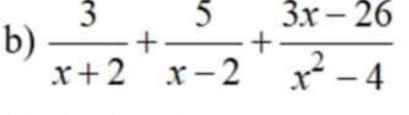 Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ
Cho mình xin lời giải chi tiết luôn ạ cực gấp xin cảm ơn ạ

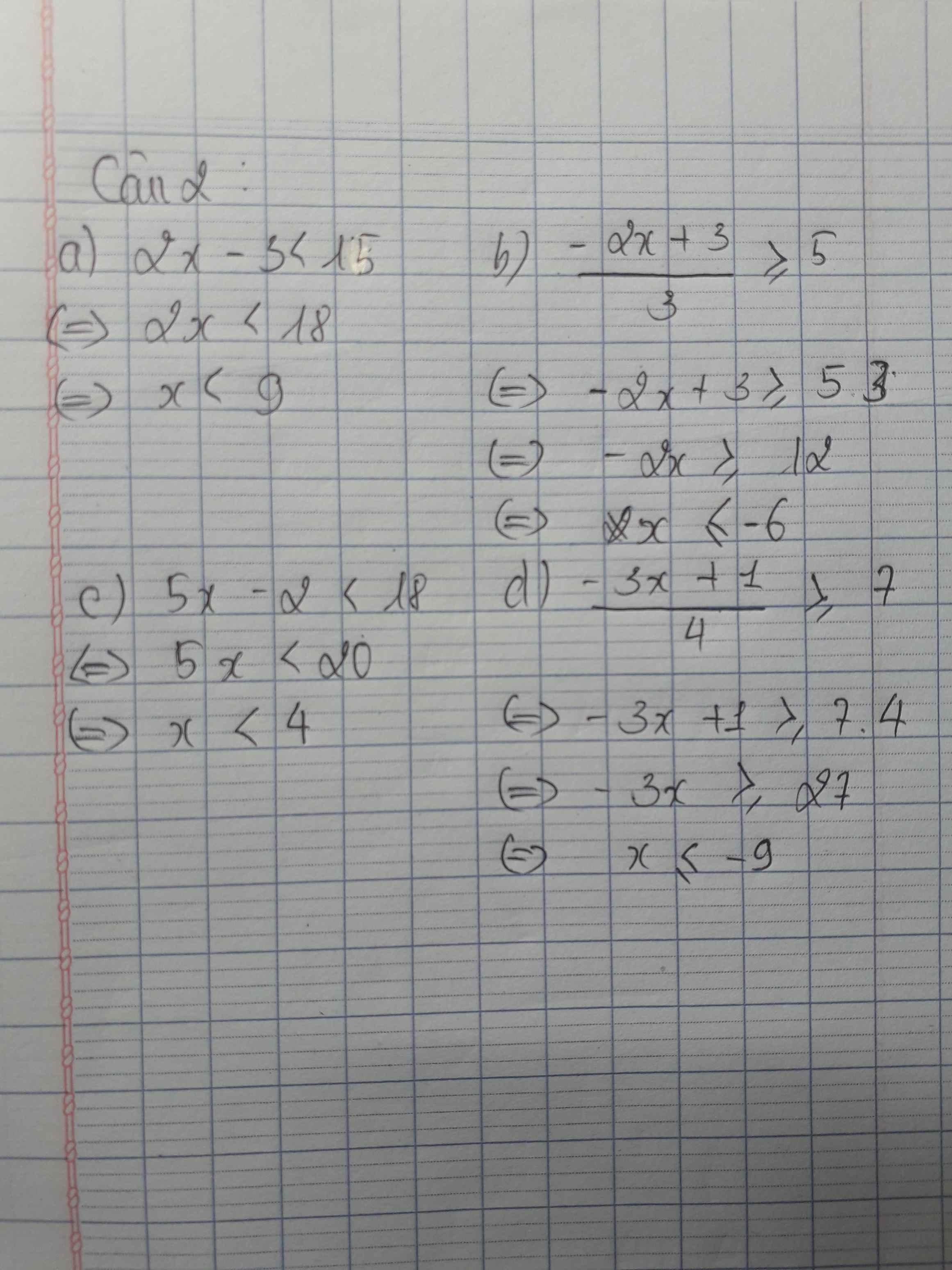



 Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ

ĐKXĐ: \(x\ne\pm2\)
\(\dfrac{2}{x-2}+\dfrac{3}{x+2}+\dfrac{18-5x}{4-x^2}=\dfrac{2\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4+3x-6+5x-18}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10x-20}{\left(x-2\right)\left(x+2\right)}=\dfrac{10\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{10}{x+2}\)