Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left\{{}\begin{matrix}xy-3x+2y-6=xy+1\\2x+2y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2y-3x=7\\2x+2y=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{5}\\y=\dfrac{29}{10}\end{matrix}\right.\)


Giải hệ pt sau \(\left\{{}\begin{matrix}x^2-xy+y^2=3\\z^2+yz+1=0\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\left(x-y\right)^2+xy=3\left(x-y\right)\\\left(x-y\right)^2+3xy=7\left(x-y\right)^3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3\left(x-y\right)^2+3xy=9\left(x-y\right)\\\left(x-y\right)^2+3xy=7\left(x-y\right)^3\end{matrix}\right.\)
\(\Rightarrow7\left(x-y\right)^3-9\left(x-y\right)=-2\left(x-y\right)^2\)
\(\Leftrightarrow7\left(x-y\right)^3+2\left(x-y\right)^2-9\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(7\left(x-y\right)^2+2\left(x-y\right)-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-y=0\\x-y=1\\x-y=\dfrac{-9}{7}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=x\\y=x-1\\y=x+\dfrac{9}{7}\end{matrix}\right.\)
TH1: \(y=x\) thay vaò pt đầu:
\(x^2-x^2+x^2=3\left(x-x\right)\Rightarrow x^2=0\Rightarrow\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\)
TH2: \(y=x-1\) thay vào pt đầu:
\(x^2-x\left(x-1\right)+\left(x-1\right)^2=3\Leftrightarrow x^2-x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow y=1\\x=-1\Rightarrow y=-2\end{matrix}\right.\)
TH3: \(y=x+\dfrac{9}{7}\):
\(x^2-x\left(x+\dfrac{9}{7}\right)+\left(x+\dfrac{9}{7}\right)^2=\dfrac{-27}{7}\Leftrightarrow x^2+\dfrac{9}{7}x+\dfrac{270}{49}=0\) (vô nghiệm)
Vậy hệ đã cho có 3 cặp nghiệm:
\(\left(x;y\right)=\left(0;0\right);\left(2;1\right);\left(-1;-2\right)\)
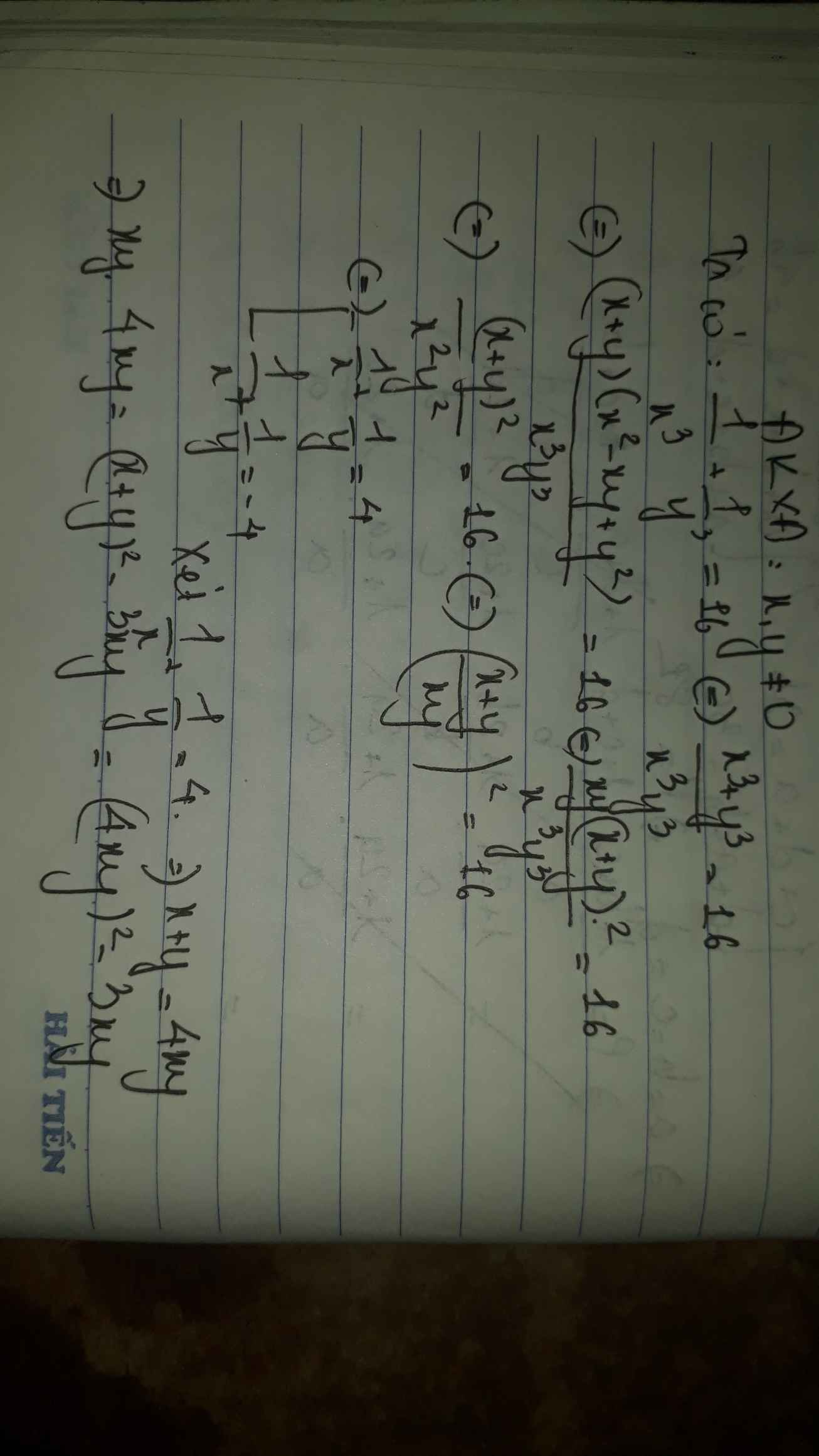
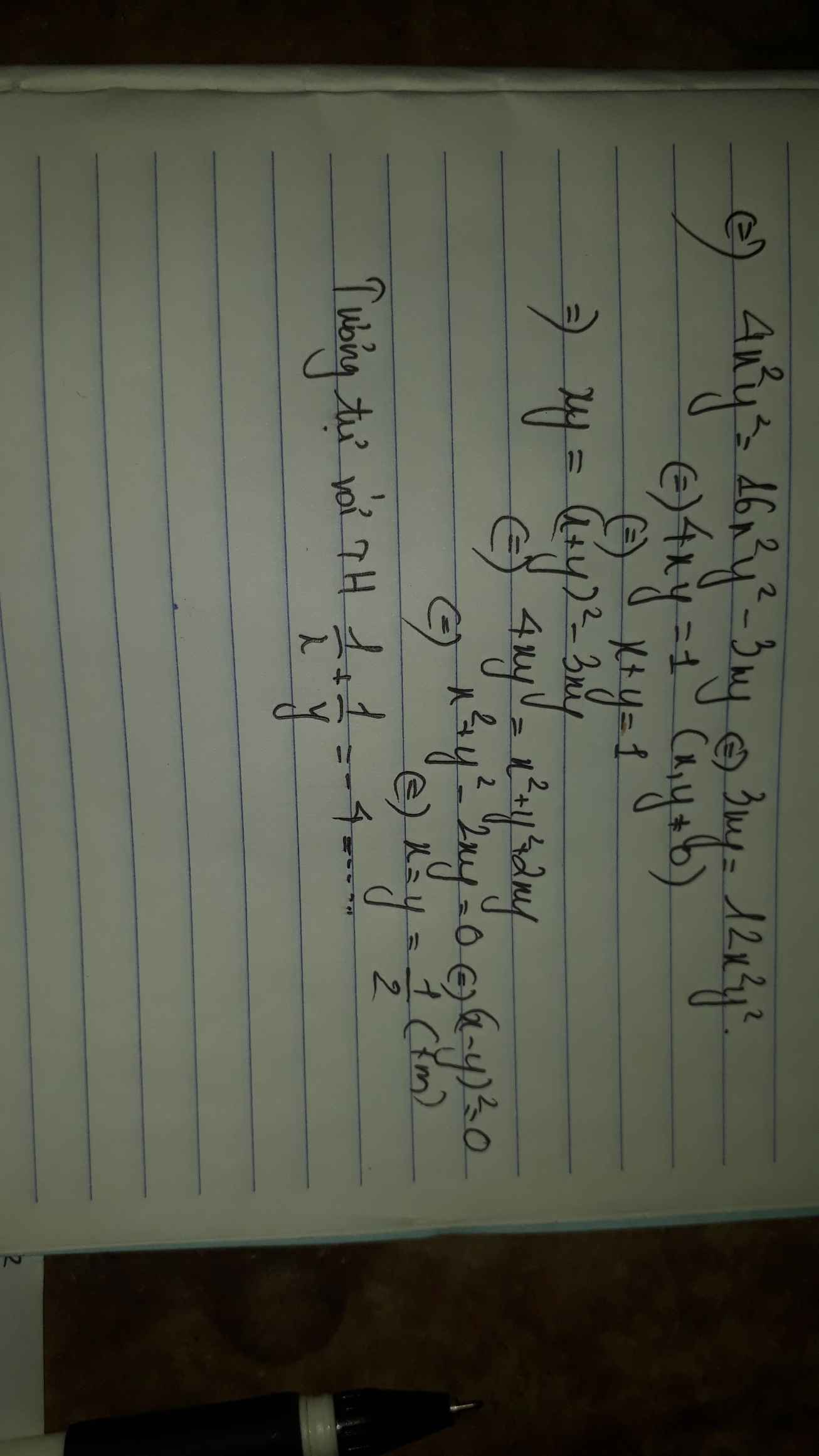

Cộng vế với vế:
\(x^2+2xy+y^2+x+y=6\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x+y\right)-6=0\)
\(\Rightarrow\left[{}\begin{matrix}x+y=-3\\x+y=2\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x+y=-3\\xy=5\end{matrix}\right.\)
Theo Viet đảo, x và y là nghiệm của:
\(t^2+3t+5=0\) (vô nghiệm)
TH2: \(\left\{{}\begin{matrix}x+y=2\\xy=0\end{matrix}\right.\)
Theo Viet đảo, x và y là nghiệm:
\(t^2-2t=0\Rightarrow\left[{}\begin{matrix}t=0\\t=2\end{matrix}\right.\)
\(\Rightarrow\left(x;y\right)=\left(2;0\right);\left(0;2\right)\)