
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường thẳng \(\Delta:\left\{{}\begin{matrix}x=1+4t\\y=2-3t\end{matrix}\right.\) đi qua điểm \(A\left(1;2\right)\) và có VTCP \(\overrightarrow{u}=\left(4;-3\right)\)
\(\Rightarrow\overrightarrow{n}=\left(3;4\right)\) là VTPT của đường thẳng
\(\Rightarrow\) PT tổng quát: \(3\left(x-1\right)+4\left(y-2\right)=0\Leftrightarrow3x+4y-11=0\)
\(\Rightarrow d\left(M;\Delta\right)=\dfrac{\left|3.1+4.\left(-1\right)-11\right|}{\sqrt{3^2+4^2}}=\dfrac{12}{5}\)

ĐKXĐ: ...
Với \(\left[{}\begin{matrix}x=0\\y=0\end{matrix}\right.\) ko phải nghiệm
\(\Leftrightarrow\left\{{}\begin{matrix}2-\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{y}}\\2+\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{x}}\end{matrix}\right.\)
Lần lượt cộng vế với vế và trừ vế cho vế 2 pt ta được:
\(\left\{{}\begin{matrix}2=\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\\\dfrac{1}{2x+y}=\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\end{matrix}\right.\)
Nhân vế với vế:
\(\dfrac{2}{2x+y}=\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\right)\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\right)\)
\(\Leftrightarrow\dfrac{2}{2x+y}=\dfrac{1}{x}-\dfrac{1}{y}\)
\(\Leftrightarrow2x^2+xy-y^2=0\)
\(\Leftrightarrow\left(x+y\right)\left(2x-y\right)=0\)
\(\Leftrightarrow...\)



\(x^3-6x+9=0\\ \Leftrightarrow x^3+3x^2-3x^2-9x+3x+9=0\\ \Leftrightarrow x^2\left(x+3\right)-3x\left(x+3\right)+3\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-3x+3\right)=0\\ \left[{}\begin{matrix}x=-3\\x^2-3x+3=0\end{matrix}\right.\)
PT dưới vô nghiệm do \(\Delta=3^2-4\cdot3< 0\).
Suy ra PT ban đầu nghiệm duy nhất \(x=-3\).
Chúc bạn học tốt nha![]()

Trừ vế theo vế hai phương trình trên ta có phương trình:
\(y^2-x^2=x^3-y^3-4x^2+4y^2+3x-3y\)
\(\Leftrightarrow\left(x^3-y^3\right)-3\left(x^2-y^2\right)+\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2-3x-3y+3\right)=0\)(1)
\(\Leftrightarrow\orbr{\begin{cases}x-y=0\\x^2+xy+y^2-3x-3y+3=0\end{cases}}\)
+)Với \(x-y=0\Leftrightarrow x=y\)
Thế vào 1 trong 2 phương trình ba đầu:
Ta có: \(x^2=x^3-4x^2+3x\Leftrightarrow x^3-5x^2+3x=0\Leftrightarrow x\left(x^2-5x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{5+\sqrt{13}}{2}hoacx=\frac{5-\sqrt{13}}{2}\end{cases}}\)
=> y tự làm nhé
+) Với \(x^2+xy+y^2-3x-3y+3=0\)
Ta có: \(x^2+xy+y^2-3x-3y+3=\left(x^2+2.x.\frac{y}{2}+\frac{y^2}{4}\right)-3\left(x+\frac{y}{2}\right)+\frac{3y^2}{4}-\frac{3y}{2}+3\)
\(=\left(x+\frac{y}{2}\right)^2-2.\left(x+\frac{y}{2}\right).\frac{3}{2}+\frac{9}{4}+3\left(\frac{y^2}{4}-2.\frac{y}{2}.\frac{1}{2}+\frac{1}{4}\right)-\frac{9}{4}-\frac{3}{4}+3\)
\(=\left(x+\frac{y}{2}-\frac{3}{2}\right)^2+3\left(\frac{y}{2}-\frac{1}{2}\right)^2\ge0\)
"=" xảy ra khi và chỉ khi : \(\hept{\begin{cases}x+\frac{y}{2}-\frac{3}{2}=0\\\frac{y}{2}-\frac{1}{2}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=1\end{cases}}\)
Thế vào 1 trong hai phương trình ban đầu thấy ko thỏa mãn : 1^2=1^3-4.1^2+3.1 vô lí
Kết luận nghiệm:...

ĐKXĐ: \(\left[{}\begin{matrix}x\ge7\\x\le-2\end{matrix}\right.\)
- Nếu \(2x-1< 0\Leftrightarrow x< \frac{1}{2}\) thì \(\left\{{}\begin{matrix}VT\ge0\\VP< 0\end{matrix}\right.\) BPT hiển nhiên đúng
Kết hợp điều kiện đề bài ta được \(x\le-2\)
- Nếu \(2x-1\ge0\Rightarrow x\ge\frac{1}{2}\) hai vế BPT đều ko âm, bình phương 2 vế:
\(\Leftrightarrow x^2-5x-14\ge4x^2-4x+1\)
\(\Leftrightarrow3x^2+x+15\le0\) (vô nghiệm)
Vậy nghiệm của BPT đã cho là \(x\le-2\)

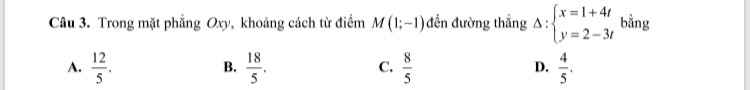

2.
a, Theo định lí hàm số sin:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow sinA=\dfrac{b}{a}sinB=\dfrac{c}{a}sinC\)
Khi đó: \(2sinA=sinB+sinC\)
\(\Leftrightarrow2sinA=\dfrac{b}{a}sinA+\dfrac{c}{a}sinA\)
\(\Leftrightarrow2=\dfrac{b}{a}+\dfrac{c}{a}\)
\(\Leftrightarrow b+c=2a\) đúng theo giả thiết
\(\Rightarrowđpcm\)
b, Ta có \(S_{ABC}=\dfrac{1}{2}a.h_a=\dfrac{1}{2}b.h_b=\dfrac{1}{2}c.h_c\)
\(\Rightarrow\left\{{}\begin{matrix}h_a=\dfrac{2.S_{ABC}}{a}\\h_b=\dfrac{2.S_{ABC}}{b}\\h_c=\dfrac{2.S_{ABC}}{c}\end{matrix}\right.\)
Khi đó: \(\dfrac{2}{h_a}=\dfrac{1}{h_b}+\dfrac{1}{h_c}\)
\(\Leftrightarrow\dfrac{2}{\dfrac{2.S_{ABC}}{a}}=\dfrac{1}{\dfrac{2.S_{ABC}}{b}}+\dfrac{1}{\dfrac{2.S_{ABC}}{c}}\)
\(\Leftrightarrow\dfrac{a}{S_{ABC}}=\dfrac{b}{2.S_{ABC}}+\dfrac{c}{2.S_{ABC}}\)
\(\Leftrightarrow b+c=2a\) đúng theo giả thiết
\(\Rightarrowđpcm\)
VD3 mà bn ơi