
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


sao dùng đc! nhg thui tui giải đc bài này rùi! cảm ơn bn đã nhắc! :))

\(\Leftrightarrow\left\{{}\begin{matrix}2x-y=3\\2x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x=6\\2x-y=3\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(\dfrac{3}{2};0\right)\)


\(\Leftrightarrow x^2-y^2=16\)
\(\Leftrightarrow\left(x-y\right)\cdot\left(x+y\right)=16\)
XONG LẬP BẢNG LÀ RA


câu hình:
a) Vì C là điểm chính giữa cung AB \(\Rightarrow OC\bot AB\Rightarrow\angle AOC=90\)
\(\Rightarrow\angle AOC=\angle AHC\Rightarrow AOHC\) nội tiếp
b) Vì AOHC nội tiếp \(\Rightarrow\angle CHO=180-\angle CAO=180-\angle CAB=\angle CNB\)(CANB nội tiếp)
c) Xét \(\Delta CHM\) và \(\Delta ACM:\) Ta có: \(\left\{{}\begin{matrix}\angle CHM=\angle ACM=90\\\angle CMAchung\end{matrix}\right.\)
\(\Rightarrow\Delta CHM\sim\Delta ACM\left(g-g\right)\Rightarrow\dfrac{HM}{CM}=\dfrac{CM}{MA}\)
Xét \(\Delta BNM\) và \(\Delta ACM:\) Ta có: \(\left\{{}\begin{matrix}\angle BMN=\angle AMC\\\angle CAM=\angle MBN\left(ACNBnt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta BNM\sim\Delta ACM\left(g-g\right)\Rightarrow\dfrac{MN}{BM}=\dfrac{CM}{MA}\)
\(\Rightarrow\dfrac{MN}{BM}=\dfrac{MH}{CM}\) mà \(BM=CM\Rightarrow MH=MN\)
\(\Rightarrow BHCN\) là hình bình hành (2 đường chéo giao nhau tại trung điểm mỗi đường)
\(\Rightarrow\angle IHB=\angle ICN=90-\angle CNA=90-\angle CBA=45\) (C là điểm chính giữa)
mà \(\angle IHO=\angle CAO=45\Rightarrow\angle OHB=90\Rightarrow OH\bot HB\)
Ta có: \(CH^2=AH.HM\Rightarrow AH=\dfrac{CH^2}{HM}=\dfrac{NB^2}{\dfrac{1}{2}HN}=\dfrac{2BN^2}{HN}\)
Lại có: \(\angle NHB=90-\angle BHI=90-45=45\Rightarrow\Delta NHB\) vuông cân
\(\Rightarrow BN=HN\Rightarrow AH=\dfrac{2BN^2}{BN}=2BN=BN+HN\)
d) Vì \(\angle OHI=\angle BHI=45\Rightarrow HI\) là phân giác \(\angle OHB\)
\(\Rightarrow\dfrac{IO}{IB}=\dfrac{OH}{HB}\)
Xét \(\Delta OHB\) và \(\Delta CHA:\) Ta có: \(\left\{{}\begin{matrix}\angle CHA=\angle OHB=90\\\angle ACH=\angle HOB\end{matrix}\right.\)
\(\Rightarrow\Delta OHB\sim\Delta CHA\left(g-g\right)\Rightarrow\dfrac{OH}{HB}=\dfrac{CH}{AH}=\dfrac{BN}{BN+HN}=\dfrac{BN}{2BN}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{IO}{IB}=\dfrac{1}{2}\Rightarrow IB=2IO\)

câu 5 ta có: \(2021\left(x^2+y^2+z^2\right)=3xyz\)
\(=>\dfrac{x^2+y^2+z^2}{xyz}=\dfrac{3}{2021}< =>\dfrac{x}{yz}+\dfrac{y}{xz}+\dfrac{z}{xy}=\dfrac{3}{2021}\)
Áp dụng BDT Cô si
\(=>\left\{{}\begin{matrix}\dfrac{x}{yz}+\dfrac{y}{xz}\ge\dfrac{2}{z}\\\dfrac{y}{xz}+\dfrac{z}{xy}\ge\dfrac{2}{x}\\\dfrac{x}{yz}+\dfrac{z}{xy}\ge\dfrac{2}{y}\end{matrix}\right.\)\(\)
\(=>\left(\dfrac{x}{yz}+\dfrac{y}{xz}\right)+\left(\dfrac{y}{xz}+\dfrac{z}{xy}\right)+\left(\dfrac{x}{yz}+\dfrac{z}{xy}\right)\ge2\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
\(=>\dfrac{x}{yz}+\dfrac{y}{xz}+\dfrac{z}{xy}\ge\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)
\(=>\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\le\dfrac{3}{2021}\)
Áp dụng cố si \(=>x^2+yz\ge2x\sqrt{yz}=>\dfrac{x}{x^2+yz}\le\dfrac{1}{2\sqrt{yz}}=\dfrac{1}{4}.2.\dfrac{1}{\sqrt{y}}.\dfrac{1}{\sqrt{z}}\)\(=\dfrac{1}{4}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)\)(1)
tương tự \(=>\dfrac{y}{y^2+zx}\le\dfrac{1}{4}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)\left(2\right)\)
\(\dfrac{z}{z^2+xy}\le\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(3\right)\)
cộng vế (1)(2)(3)
\(=>A\le\dfrac{1}{4}\left[\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}+\dfrac{1}{x}+\dfrac{1}{z}+\dfrac{1}{y}\right]\)\(=\dfrac{1}{4}.2\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)\)
\(=\dfrac{1}{2}.\dfrac{3}{2021}=\dfrac{3}{4042}\). Dấu"=" xảy ra<=>\(x=y=z=\dfrac{1}{2021}\)
vậy Max \(=\dfrac{3}{4042}\)








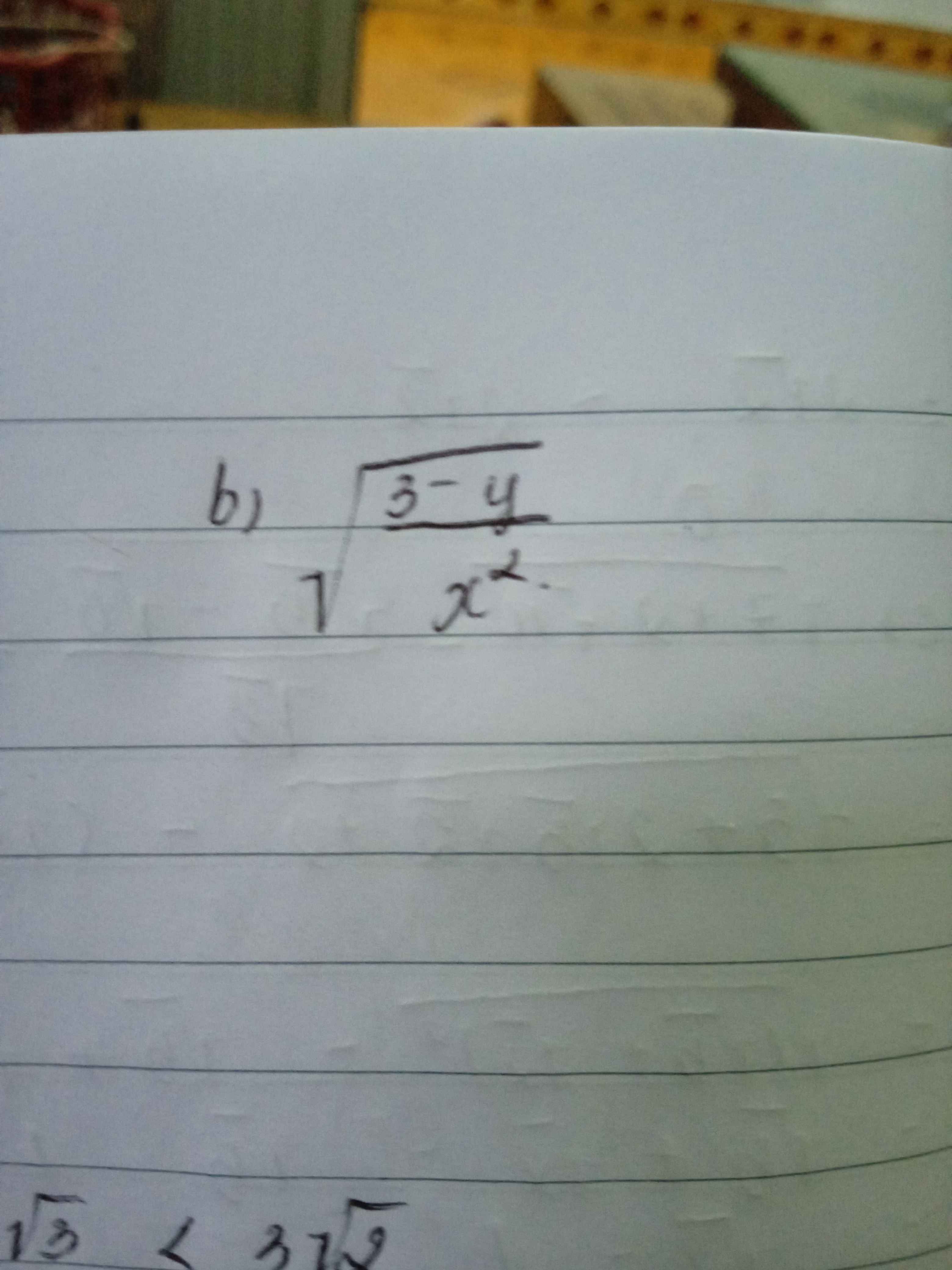
a) Gọi vận tốc xuôi dòng là \(x\left(km/h\right),x>20\).
Theo bài ra, ta có phương trình:
\(\frac{120}{x}+\frac{120}{x-20}=5\)
\(\Rightarrow120\left(x-20\right)+120x=5x\left(x-20\right)\)
\(\Leftrightarrow x^2-68x+480=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=60\left(tm\right)\\x=8\left(l\right)\end{cases}}\)
b) \(\hept{\begin{cases}x-my=2-4m\\mx+y=3m+1\end{cases}}\)
Với \(m=0\): \(\hept{\begin{cases}x=2\\y=1\end{cases}}\)
Dễ thấy thỏa mãn.
Với \(m\ne0\):
\(\hept{\begin{cases}x-my=2-4m\\mx+y=3m+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x-my=2-4m\\m^2x+my=3m^2+m\end{cases}}\Rightarrow\left(m^2+1\right)x=3m^2-3m+2\)
\(\Leftrightarrow x=\frac{3m^2-3m+2}{m^2+1}\Rightarrow y=3m+1-mx=\frac{4m^2+m+1}{m^2+1}\)
suy ra đpcm.
Ta có:
\(\hept{\begin{cases}x_0-my_0=2-4m\\mx_0+y_0=3m+1\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0-2=m\left(y_0-4\right)\\y_0-1=m\left(3-x_0\right)\end{cases}}\)
\(\Rightarrow\frac{x_0-2}{y_0-1}=\frac{y_0-4}{3-x_0}\Rightarrow\left(x_0-2\right)\left(3-x_0\right)=\left(y_0-4\right)\left(y_0-1\right)\)
\(\Leftrightarrow-x_0^2+5x_0-6=y_0^2-5y_0+4\)
\(\Leftrightarrow x_0^2+y_0^2-5\left(x_0+y_0\right)+10=0\)