Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`1.` Với `0=0(` luôn đúng `)` `->` Kết luận: Vậy `S={x|x\inRR}`
`2.` Với `-1>0(` vô lý `)` `->` Kết luận: Vậy `S=∅`

Phương trình chứa ẩn ở mẫu thì phải có ĐKXĐ để mẫu khác 0, và phải khử mẫu và còn phải loại những giá trị không thỏa mãn ĐK
Phương trình không chứa ẩn ở mẫu thì chỉ cần giải phương trình như bình thường

bạn cứ ghi là:
Vậy phương trình có tập nghiệm: S={0}
hoặc
Vậy phương trình có nghiệm: x = 0
bỏ cái x=0 đi
0x=1(vô lý)
xong kết luận là : vậy phương trình vô nghiệm

Answer:
e) \(\frac{x-3}{x-2}-\frac{x-2}{x-4}=3\frac{1}{5}\left(ĐK:x\ne2;x\ne4\right)\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(x-4\right)-\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x-4\right)}=\frac{16}{5}\)
\(\Leftrightarrow x^2-7x+12-x^2+4x-4=\frac{16}{5}.\left(x-2\right)\left(x-4\right)\)
\(\Leftrightarrow-3x+8=\frac{16}{5}.\left(x^2-6x+8\right)\)
\(\Leftrightarrow-3x+8=\frac{16}{5}x^2-\frac{96}{5}x+\frac{128}{5}\)
\(\Leftrightarrow-\frac{16}{5}x^2+\frac{81}{5}x-\frac{88}{5}=0\)
\(\Leftrightarrow-\frac{16}{5}.\left(x^2-\frac{81}{16}x+\frac{11}{2}\right)=0\)
\(\Leftrightarrow x^2-\frac{81}{16}x+\frac{6561}{1024}-\frac{929}{1024}=0\)
\(\Leftrightarrow\left(x-\frac{81}{32}\right)^2=\frac{929}{1024}\)
\(\Leftrightarrow\orbr{\begin{cases}x-\frac{81}{32}=\frac{\sqrt{929}}{32}\\x-\frac{81}{32}=-\frac{\sqrt{929}}{32}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{81+\sqrt{929}}{32}\\x=\frac{81-\sqrt{929}}{32}\end{cases}}}\)
f) \(\frac{x-3}{x-2}+\frac{x-2}{x-4}=-1\left(ĐK:x\ne2;x\ne4\right)\)
\(\Leftrightarrow\frac{\left(x-3\right)\left(x-4\right)+\left(x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x-4\right)}=\frac{-\left(x-2\right)\left(x-4\right)}{\left(x-2\right)\left(x-4\right)}\)
\(\Leftrightarrow x^2-4x-3x+12+x^2-4x+4=-x^2+4x+2x-8\)
\(\Leftrightarrow x^2+x^2+x^2-4x-3x-4x-4x-2x+12+4+8=0\)
\(\Leftrightarrow3x^2-9x-8x+24=0\)
\(\Leftrightarrow3x\left(x-3\right)-8\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(3x-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\3x-8=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=\frac{8}{3}\end{cases}}}\)

a: ĐKXĐ: x<>1
\(PT\Leftrightarrow1+\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)^2}=0\)
=>\(\dfrac{\left(x-1\right)^2+x-1+x}{\left(x-1\right)^2}=0\)
=>x^2-2x+1+2x-1=0
=>x^2=0
=>x=0
b: ĐKXĐ: x<>1
Đề sai rồi bạn, sao lại có hai dấu bằng kìa

Khi giải phương trình chứa ẩn ở mẫu, ta phải chú ý đến điều kiện xác định của phương trình.

Các pt a,c,d và pt bậc nhất 1 ẩn
a: a=1; b=2
c: a=-2; b=1
d: a=3; b=0

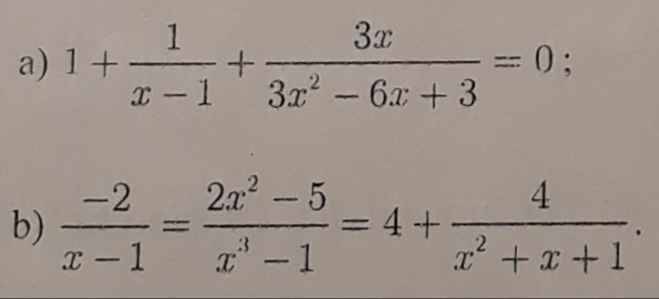
Thì kết luận tập nghiệm là tất cả các số trừ các số không thỏa ĐKXĐ