Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt pt là (1)
Ta có :
(1) <=> \(\left[\left(x-3\right)\left(x-10\right)\right]\left[\left(x-5\right)\left(x-6\right)\right]-24x^2=0\)
\(\Leftrightarrow\left(x^2-13x+30\right)\left(x^2-11x+30\right)-24x^2=0\)
Đặt \(x^2-12x+30=t\) (*)
Phương trình trở thành \(\left(t-x\right)\left(t+x\right)-24x^2=0\)
\(\Leftrightarrow t^2-x^2-24x^2=0\)
\(\Leftrightarrow t^2-25x^2=0\)
\(\Leftrightarrow\left(t-5x\right)\left(t+5x\right)=0\)
Thay (*) vào ta có :
\(\left(x^2-17x+30\right)\left(x^2+7x+30\right)=0\)
Để ý thấy \(x^2-7x+30\ne0\)
\(\Rightarrow x^2-17x+30=0\)
\(\Leftrightarrow x^2-15x-2x+30=0\)
\(\Leftrightarrow x\left(x-15\right)-2\left(x-15\right)=0\)
\(\Leftrightarrow\left(x-15\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=15\end{matrix}\right.\)
Vậy S={1 ; 15 }

a)
\((x-3)(x-5)(x-6)(x-10)=24x^2\)
\(\Leftrightarrow [(x-3)(x-10)][(x-5)(x-6)]=24x^2\)
\(\Leftrightarrow (x^2-13x+30)(x^2-11x+30)=24x^2\)
Đặt \(x^2-11x+30=a\). PT trở thành:
\((a-2x)a=24x^2\)
\(\Leftrightarrow a^2-2ax-24x^2=0\)
\(\Leftrightarrow a^2-6ax+4ax-24x^2=0\)
\(\Leftrightarrow a(a-6x)+4x(a-6x)=0\)
\(\Leftrightarrow (a+4x)(a-6x)=0\)
\(\Rightarrow \left[\begin{matrix} a+4x=0\\ a-6x=0\end{matrix}\right.\Rightarrow \left[\begin{matrix} x^2-7x+30=0\\ x^2-17x+30=0\end{matrix}\right.\)
\(\Rightarrow \left[\begin{matrix} (x-3,5)^2+17,75=0(\text{vô lý})\\ (x-15)(x-2)=0\end{matrix}\right.\)
\(\Rightarrow x=15\) hoặc $x=2$
b)
Đặt \(x-7=a\). PT trở thành:
\((a+1)^4+(a-1)^4=272\)
\(\Leftrightarrow a^4+4a^3+6a^2+4a+1+a^4-4a^3+6a^2-4a+1=272\)
\(\Leftrightarrow 2a^4+12a^2+2=272\)
\(\Leftrightarrow a^4+6a^2-135=0\)
\(\Leftrightarrow (a^2+3)^2-144=0\Leftrightarrow (a^2+3)^2-12^2=0\)
\(\Leftrightarrow (a^2+15)(a^2-9)=0\)
\(\Rightarrow a^2-9=0\Rightarrow a=\pm 3\)
\(\Rightarrow x=a+7=\left[\begin{matrix} 4\\ 10\end{matrix}\right.\)

a) \(8 - \left( {x - 15} \right) = 2.\left( {3 - 2x} \right)\)
\(8 - x + 15 = 6 - 4x\)
\( - x + 4x = 6 - 8 - 15\)
\(3x = - 17\)
\(x = \left( { - 17} \right):3\)
\(x = \dfrac{{ - 17}}{3}\)
Vậy nghiệm của phương trình là \(x = \dfrac{{ - 17}}{3}\).
b) \( - 6\left( {1,5 - 2u} \right) = 3\left( { - 15 + 2u} \right)\)
\( - 9 + 12u = - 45 + 6u\)
\(12u - 6u = - 45 + 9\)
\(u = \left( { - 36} \right):6\)
\(6u = - 36\)
\(u = - 6\)
Vậy nghiệm của phương trình là \(u = - 6\).
c) \({\left( {x + 3} \right)^2} - x\left( {x + 4} \right) = 13\)
\(\left( {{x^2} + 6x + 9} \right) - \left( {{x^2} + 4x} \right) = 13\)
\({x^2} + 6x + 9 - {x^2} - 4x = 13\)
\(\left( {{x^2} - {x^2}} \right) + \left( {6x - 4x} \right) = 13 - 9\)
\(2x = 4\)
\(x = 4:2\)
\(x = 2\)
Vậy nghiệm của phương trình là \(x = 2\).
d) \(\left( {y + 5} \right)\left( {y - 5} \right) - {\left( {y - 2} \right)^2} = 5\)
\(\left( {{y^2} - 25} \right) - \left( {{y^2} - 4y + 4} \right) = 5\)
\({y^2} - 25 - {y^2} + 4y - 4 = 5\)
\(\left( {{y^2} - {y^2}} \right) + 4y = 5 + 4 + 25\)
\(4y = 34\)
\(y = 34:4\)
\(y = \dfrac{{17}}{2}\)
Vậy nghiệm của phương trình là \(y = \dfrac{{17}}{2}\).

1) \(2\left(x+3\right)>5\left(x-1\right)+2\Leftrightarrow2x+6>5x-5+2\Leftrightarrow3x>9\Leftrightarrow x>3\)
2) \(x^2-x\left(x+2\right)>3x-10\)
\(\Leftrightarrow x^2-x^2-2x>3x-10\Leftrightarrow5x< 10\Leftrightarrow x< 2\)
3) \(x\left(x-5\right)< \left(x+1\right)^2\)
\(\Leftrightarrow x^2-5x< x^2+2x+1\Leftrightarrow7x>-1\Leftrightarrow x>-\dfrac{1}{7}\)
4) \(15-2\left(x-7\right)< 2\left(x-3\right)-6\)
\(\Leftrightarrow15-2x+14< 2x-6-6\Leftrightarrow4x>41\Leftrightarrow x>\dfrac{41}{4}\)
1: Ta có: \(2\left(x+3\right)>5\left(x-1\right)+2\)
\(\Leftrightarrow2x+6>5x-5+2\)
\(\Leftrightarrow-3x>-9\)
hay x<3
2: Ta có: \(x^2-x\left(x+2\right)>3x-10\)
\(\Leftrightarrow x^2-x^2-2x>3x-10\)
\(\Leftrightarrow-5x>-10\)
hay x<2
3: Ta có: \(x\left(x-5\right)\le\left(x+1\right)^2\)
\(\Leftrightarrow x^2-5x-x^2-2x-1\ge0\)
\(\Leftrightarrow-7x\ge1\)
hay \(x\le-\dfrac{1}{7}\)

ĐKXĐ: \(x\notin\left\{-1;-2;-3;-4\right\}\)
Ta có: \(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{x+4}{\left(x+1\right)\left(x+4\right)}-\dfrac{x+1}{\left(x+1\right)\left(x+4\right)}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{x+4-x-1}{\left(x+1\right)\left(x+4\right)}=\dfrac{x^2+5x+4}{6\left(x+1\right)\left(x+4\right)}\)
\(\Leftrightarrow\dfrac{18}{6\left(x+1\right)\left(x+4\right)}=\dfrac{x^2+5x+4}{6\left(x+1\right)\left(x+4\right)}\)
Suy ra: \(x^2+5x+4=18\)
\(\Leftrightarrow x^2+5x-14=0\)
\(\Leftrightarrow x^2+7x-2x-14=0\)
\(\Leftrightarrow x\left(x+7\right)-2\left(x+7\right)=0\)
\(\Leftrightarrow\left(x+7\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+7=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
Vậy: S={-7;2}

(x-3)(x-5)(x-6)(x-10)-24x2
=(x-3)(x-10)(x-5)(x-6)-24x2
=(x2-13x+30)(x2-11x+30)-24x2
Đặt x2-12x+30=k
Khi đó ta có:
(k-x)(k+x)-24x2=k2-x2-24x2=k2-25x2
=(k-5x)(k+5x)
=(x2-12x+30-5x)(x2-12x+30+5x)
=(x2-17x+30)(x2-7x+30)
=(x2-2x-15x+30)(x2-7x+30)
=(x-2)(x-15)(x2-7x+30)

\(1,\) thiếu đề
\(2,\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)
\(\Leftrightarrow\dfrac{5\left(5x+2\right)}{30}-\dfrac{10\left(8x-1\right)}{30}=\dfrac{6\left(4x+2\right)}{30}-\dfrac{150}{30}\)
\(\Leftrightarrow5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)
\(\Leftrightarrow25x+10-80x+10=24x+12-150\)
\(\Leftrightarrow-55x+20=24x-138\)
\(\Leftrightarrow24x-138+55x-20=0\)
\(\Leftrightarrow79x-158=0\)
\(\Leftrightarrow x=2\)
\(3,ĐKXĐ:\left\{{}\begin{matrix}x\ne1\\x\ne-1\\x\ne3\end{matrix}\right.\\ \dfrac{x}{2x-6}+\dfrac{x}{2x-2}=\dfrac{-2x}{\left(x+1\right)\left(3-x\right)}\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(3-x\right)}=0\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}-\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=0\)
\(\Leftrightarrow x\left(\dfrac{1}{2\left(x-3\right)}+\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{\left(x+1\right)\left(x-3\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4\left(x-1\right)}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{x^2-1}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{x^2-2x-3}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4x-4}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x.\dfrac{x^2-1+x^2-2x-3-4x+4}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x^2-6x}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x\left(x-3\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{x}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x=0\)
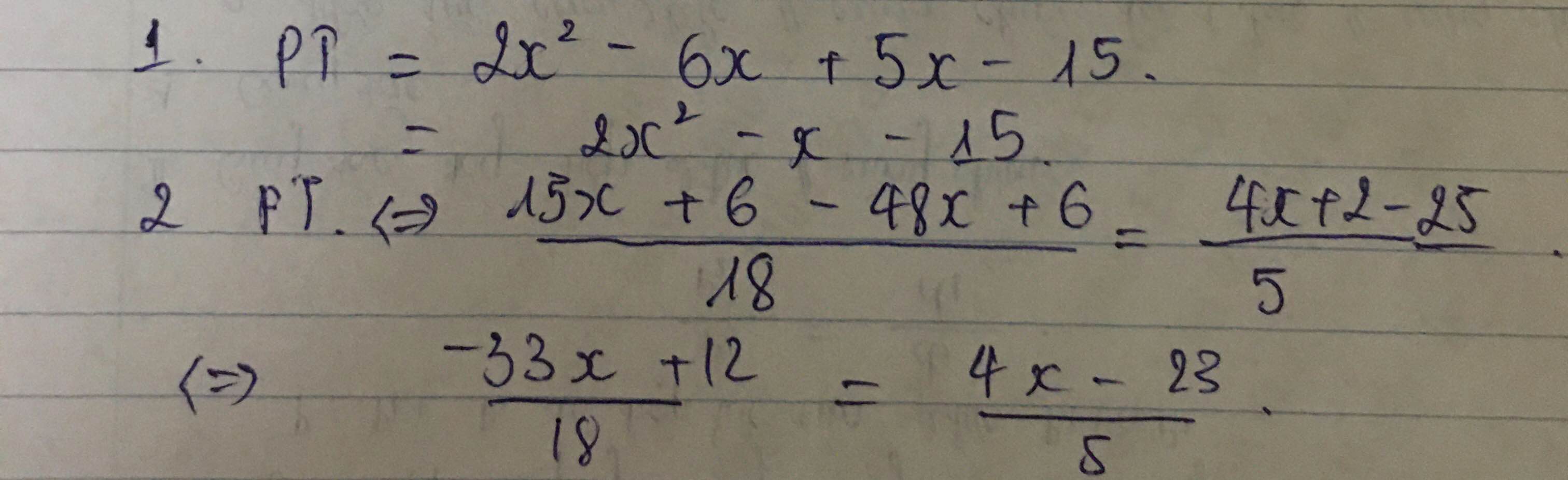
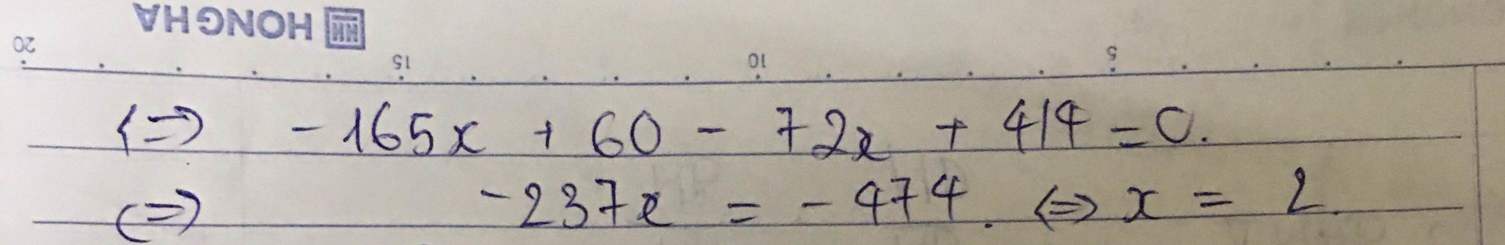
\(\left(x-3\right)\left(x-5\right)\left(x-6\right)\left(x-10\right)=24x^2\) (1)
\(\Leftrightarrow\left(x^2-5x-3x+15\right)\left(x-6\right)\left(x-10\right)=24x^2\)
\(\Leftrightarrow\left(x^2-8x+15\right)\left(x-6\right)\left(x-10\right)=24x^2\)
\(\Leftrightarrow\left(x^3-6x^2-8x^2+48x+15x-90\right)\left(x-10\right)=24x^2\)
\(\Leftrightarrow\left(x^3-14x^2+63x-90\right)\left(x-10\right)=24x^2\)
\(\Leftrightarrow x^4-10x^3-14x^3+140x^2+63x^2-630x-90x+900=24x^2\)
\(\Leftrightarrow x^4-2x^3-22x^3+44x^2+135x^2-270x-450x+900=0\)
\(\Leftrightarrow x^3\left(x-2\right)-22x^2\left(x-2\right)+135x\left(x-2\right)-450\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3-22x^2+135x-450\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3-15x^2-7x^2+105x+30x-450\right)=0\)
\(\Leftrightarrow\left(x-2\right)\cdot\left[x^2\cdot\left(x-15\right)-7x\left(x-15\right)+30\left(x-15\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-15\right)\left(x^2-7x+30\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-15=0\\x^2-7x+30=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=15\\x\notin R\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=15\end{matrix}\right.\)
Vậy tập nghiệm phương trình (1) là \(S=\left\{2;15\right\}\)
PT\(\Leftrightarrow\)\(\left[\left(x-3\right)\left(x-10\right)\right]\left[\left(x-5\right)\left(x-6\right)\right]=24x^2\)
\(\Leftrightarrow\)\(\left(x^2-13x+30\right)\left(x^2-11x+30\right)=24x^2\)
Nhận thấy x=0 không là nghiệm của PT. Chia cả hai vế của phương trình cho \(x^2\) ta được:
PT\(\Leftrightarrow\)\(\left(x-13+\dfrac{30}{x}\right)\left(x-11+\dfrac{30}{x}\right)=24\)
Đặt \(x+\dfrac{30}{x}=t\) (1)
PT\(\Leftrightarrow\)\(\left(t-13\right)\left(t-11\right)=24\)
Tìm được \(\left[{}\begin{matrix}t=17\\t=7\end{matrix}\right.\)
Thay vào (1):\(\left[{}\begin{matrix}x^2-17x+30=0\\x^2-7x+30=0\end{matrix}\right.\)
Tìm được \(\left[{}\begin{matrix}x=15\\x=2\end{matrix}\right.\)