
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ko vt lại đề
4x2-8x+x-2=0
=>4x(x-2)+(x-2)=0
=>(x-2)(4x+1)=0
......
b) bn tự làm nha
a)\(4x^2-7x-2=0\)
Ta có \(\Delta=7^2+4.4.2=81,\sqrt{\Delta}=9\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{7+9}{8}=2\\x=\frac{7-9}{8}=\frac{-1}{4}\end{cases}}\)
b)\(4x^2+5x-6=0\)
Ta có \(\Delta=5^2+4.4.6=121,\sqrt{\Delta}=11\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-5+11}{8}=\frac{3}{4}\\x=\frac{-5-11}{8}=-2\end{cases}}\)

\(2x^3+7x^2+7x+2=0\)
\(\Leftrightarrow\left(2x^3+4x^2\right)+\left(3x^2+6x\right)+\left(x+2\right)=0\)
\(\Leftrightarrow2x^2\left(x+2\right)+3x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x^2+3x+1\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[2x\left(x+1\right)+\left(x+1\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+1\right)\left(2x+1\right)=0\)
.......................................................................................
\(x^3-8x^2-8x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)-8x\left(x+1\right)=0\)
......................................................................................

Bài 4 :
24 phút = \(\dfrac{24}{60} = \dfrac{2}{5}\) giờ
Gọi thời gian dự định đi từ A đến B là x(giờ) ; x > 0
Suy ra quãng đường AB là 36x(km)
Khi vận tốc sau khi giảm là 36 -6 = 30(km/h)
Vì giảm vận tốc nên thời gian đi hết AB là x + \(\dfrac{2}{5}\)(giờ)
Ta có phương trình:
\(36x = 30(x + \dfrac{2}{5})\\ \Leftrightarrow x = 2\)
Vậy quãng đường AB dài 36.2 = 72(km)

\(a)x^3-\frac{x}{49}=0\)
\(\Leftrightarrow x\left(x^2-\frac{1}{7^2}\right)=0\)
\(\Leftrightarrow x=0\)Hoặc \(x^2-\frac{1}{7^2}=0\)
TH1: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x=\frac{0}{x^2-\frac{1}{7^2}}\\ \Leftrightarrow x=0\)
TH2: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x^2-\frac{1}{7^2}=\frac{0}{x}\\ x^2=0+\frac{1}{7^2}\\ x^2=\frac{1}{7^2}\\ x^2=\left(\frac{1}{7}\right)^2\\ \Leftrightarrow x=\frac{1}{7}\)
Vậy \(x=0\)Hoặc \(x=\frac{1}{7}\)
a) x3 - x/49 = 0
<=> x(x2 - 1/49) = 0
<=> x = 0 hoặc x2 - 1/49 = 0
<=> x = 0 hoặc x = +1/7
b) x2 - 7x + 12 = 0
<=> (x - 3)(x - 4) = 0
<=> x - 3 = 0 hoặc x - 4 = 0
<=> x = 3 hoặc x = 4
c) 4x2 - 3x - 1 = 0
<=> 4x2 + x - 4x - 1 = 0
<=> x(4x + 1) - (4x + 1) = 0
<=> (4x + 1)(x - 1) = 0
<=> 4x + 1 = 0 hoặc x - 1 = 0
<=> x = -1/4 hoặc x = 1
d) x3 - 2x - 4 = 0
<=> (x2 + 2x + 2)(x - 2) = 0
vì x2 + 2x + 2 khác 0 nên:
<=> x - 2 = 0
<=> x = 2

a: (3x-2)(4x+5)=0
=>3x-2=0 hoặc 4x+5=0
=>x=2/3 hoặc x=-5/4
b: (2,3x-6,9)(0,1x+2)=0
=>2,3x-6,9=0 hoặc 0,1x+2=0
=>x=3 hoặc x=-20
c: =>(x-3)(2x+5)=0
=>x-3=0 hoặc 2x+5=0
=>x=3 hoặc x=-5/2

a) ( 3.x + 1 ) . ( 7.x + 3 ) = (5.x-7 ) . ( 3.x + 1 )
<=> ( 3.x + 1 ) . ( 7.x + 3 ) - ( 5.x - 7) . ( 3.x + 1 ) = 0
<=> ( 3.x + 1 ) . ( 7.x + 3 - 5.x + 7 ) = 0
<=> ( 3.x + 1 ) . ( 2.x + 10 ) = 0
<=> \(\orbr{\begin{cases}3.x+1=0\\2.x+10=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{3}\\x=-5\end{cases}}}\)
Vậy x = { \(\frac{-1}{3};-5\)}
b) x2 + 10.x + 25 - 4.x . ( x + 5 ) = 0
<=> ( x + 5 )2 -4.x . (x + 5 ) = 0
<=> ( x+ 5 ) . ( x + 5 - 4.x ) = 0
<=> ( x + 5 ) . ( 5 - 3.x ) = 0
<=> \(\orbr{\begin{cases}x+5=0\\5-3.x\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{5}{3}\end{cases}}}\)
Vậy x = \(\left\{\frac{5}{3};-5\right\}\)
c) (4.x - 5 )2 - 2. ( 16.x2 -25 ) = 0
<=> ( 4.x-5)2 -2 .( 4.x-5) .( 4.x + 5 ) = 0
<=> ( 4.x -5 )2 - ( 8.x+ 10 ) . ( 4.x -5 ) = 0
<=> ( 4.x -5 ) . ( 4.x-5 - 8.x - 10 ) = 0
<=> ( 4.x - 5 ) . ( -4.x - 15 ) = 0
<=> \(\orbr{\begin{cases}4.x-5=0\\-4.x-15=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{4}\\x=\frac{-15}{4}\end{cases}}}\)
Vậy x = \(\left\{\frac{5}{4};\frac{-15}{4}\right\}\)
d) ( 4.x + 3 )2 = 4. ( x2 - 2.x + 1 )
<=> 16.x2 + 24.x + 9 - 4.x2 + 8.x - 4 = 0
<=> 12.x2 + 32.x + 5 =0
<=> 12. ( x +\(\frac{1}{8}\) ) . ( x + \(\frac{5}{2}\)) = 0
<=> \(\orbr{\begin{cases}x+\frac{1}{6}=0\\x+\frac{5}{2}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{6}\\x=\frac{-5}{2}\end{cases}}}\)
Vậy x = \(\left\{\frac{-1}{6};\frac{-5}{2}\right\}\)
e) x2 -11.x + 28 = 0
<=> x2 -4.x - 7.x + 28 = 0
<=> ( x - 7 ) . ( x - 4 ) = 0
<=> \(\orbr{\begin{cases}x-7=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=7\\x=4\end{cases}}}\)
Vậy x = { 4 ; 7 }
f ) 3.x.3 - 3.x2 - 6.x = 0
<=> 3.x. ( x2 -x - 2 ) = 0
<=> 3.x. ( x - 2 ) . ( x + 1 ) = 0
<=> \(\orbr{\begin{cases}x-2=0\\x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}}\)
\([x=0\) \([x=0\)
( Lưu ý :Lưu ý này không cần ghi vào vở : Chị nối 2 ý đó làm 1 nha cj ! )
Vậy x = { 2 ; -1 ; 0 }

3x2 + 2x - 1 = 0
=> 3x2 + 3x - x - 1 = 0
=> 3x(x + 1) - (x + 1) = 0
=> (3x - 1)(x + 1) = 0
=> \(\orbr{\begin{cases}3x-1=0\\x+1=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-1\end{cases}}\)
x2 - 5x + 6 = 0
=> x2 - 2x - 3x + 6 = 0
=> x(x - 2) - 3(x - 2) = 0
=> (x - 3)(x - 2) = 0
=> \(\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)
3x2 + 7x + 2 = 0
=> 3x2 + 6x + x + 2 = 0
=> 3x(x + 2) + (x + 2) = 0
=> (3x + 1)(x + 2) = 0
=> \(\orbr{\begin{cases}3x+1=0\\x+2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=-\frac{1}{3}\\x=-2\end{cases}}\)
1, \(3x^2+2x-1=0\Leftrightarrow3x^2+3x-x-1=0\)
\(\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}}\)
2, \(x^2-5x+6=0\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}}\)
3, \(3x^2+7x+2=0\Leftrightarrow3x^2+6x+x+2=0\)
\(\Leftrightarrow3x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{1}{3}\end{cases}}}\)
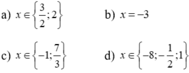


TH1 : \(1+4x\ge0;7x-2\ge0\)
\(\Rightarrow\left|1+4x\right|-\left|7x-2\right|=1+4x-7x+2=0\)
\(\Leftrightarrow3-3x=0\)
\(\Leftrightarrow x=1\)(TM)
TH2 : \(1+4x\le0;7x-2\le0\)
\(\Rightarrow\left|1+4x\right|-\left|7x-2\right|=-1-4x+7x-2=0\)
\(\Leftrightarrow3x-3=0\)
\(\Leftrightarrow x=1\)(loại) Bạn thử x = 1 vào 1 + 4x nếu 1 + 4x \(\le\)0 thì lấy còn \(\ge\)0 thì loại
TH3 : \(1+4x\ge0;7x-2\le0\)
\(\Rightarrow\left|1+4x\right|-\left|7x-2\right|=1+4x+7x-2=0\)
\(\Leftrightarrow11x-1=0\)
\(\Leftrightarrow x=\frac{1}{11}\)(TM)
TH4 : \(1+4x\le0;7x-2\ge0\)
\(\Rightarrow\left|1+4x\right|-\left|7x-2\right|=-1-4x-7x+2=0\)
\(\Leftrightarrow1-11x=0\)
\(\Leftrightarrow x=\frac{1}{11}\)(loại)
Vậy \(S=\left\{\frac{1}{11};1\right\}\)
|1+4x| - |7x-2| =0 (*)
ta có: +) 1+4x=0 =>4x =-1 =>x=-1/4
+)7x-2=0 =>7x=2 =>x =7/2
=> ta có bảng sau:
x -1/4 7/2
1+4x - 0 + | +
7x-2 - | - 0 +
TH 1: x <-1/4 => 1+4x <0 =>|1+4x|=-(1+4x)
7x-2 <0 |7x-2|=-(7x-2)
(*) =>-(1+4x)+(7x-2)=0
=>-1-4x+7x-2=0
=>-3+3x=0
=>3x=3
=>x=1 ( không t/m x < -1/4 )
TH 2: -1/4 _< x _< 7/2 => 1+4x >0 =>|1+4x|=1+4x
7x-2 <0 |7x-2|=-(7x-2)
(*) =>1+4x+(7x-2)=0
=>1+4x+7x-2=0
=>11x-1 =0
=>11x=1
=>x=1/11 ( t/m -1/4 _< x <7/2)
TH 3: 7/2 > x =>1+4x >0 => |1+4x|=1+4x
7x-2 >0 |7x-2|=7x-2
(*) => 1+4x-(7x-2)=0
=>1+4x-7x+2=0
=>3-3x=0
=>3x =3
=>x=1 ( t/m 7/2 >x)
từ 3 trường hợp trên =>x { 1/11 ;1}