Nếu $x+2>2x+1$ thì $2^{x+2}>2^{2x+1},3^{x+2}>3^{2x+1}$ nên VT>VP.

Nếu $x+2<2x+1$ thì $2^{x+2}<2^{2x+1},3^{x+2}<3^{2x+1}$ nên VT<VP.

Vậy x+2=2x+1 hay x=1

Phương trình đã cho tương đương với phương trình 

\(3^{x+2}-3^{x+2}=3^{2x+1}-2^{2x+1}\)

Dễ thấy \(x=1\) là nghiệm của phương trình

Nếu \(x>1\) thì \(x+2<2x+1\)

Do đó

\(3^{x+2}<3^{2x+1};3^{2x+1}>2^{x+2}\)

Hay vế trái <0< Vế phải, phương trình vô nghiệm

Tương tự, nếu x<1 thì phương trình cũng vô nghiệm

Vạy x=1 là nghiệm duy nhất của phương trình

ĐKXĐ: \(x>3\)

Lấy logarit 2 vế: \(\left(2x^2-7x\right).ln\left(x-3\right)>0\)

\(\Leftrightarrow x\left(2x-7\right)ln\left(x-3\right)>0\)

Bảng xét dấu:

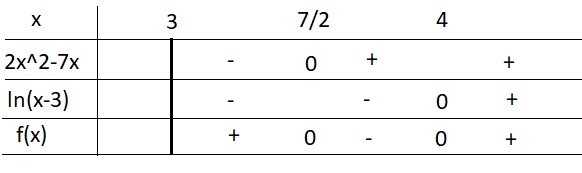
\(\Rightarrow\) Nghiệm của BPT là \(\left[{}\begin{matrix}3< x< \dfrac{7}{2}\\x>4\end{matrix}\right.\)

bài này mình chưa giải dc triệt để ở cái cuối

\(2x^3-4x^2+3x-1=2x^3\left(2-y\right)\sqrt{3-2y}\) \(\left(y\le\dfrac{3}{2}\right)\)

\(\Leftrightarrow4x^3-8x^2+6x-2=2x^3\left(4-2y\right)\sqrt{3-2y}\left(1\right)\)

\(đặt:\sqrt{3-2y}=a\ge0\Rightarrow a^2+1=4-2y\)

\(\left(1\right)\Leftrightarrow4x^3-8x^2+6x-2=2x^3.\left(a^2+1\right)a\)

\(\Leftrightarrow4x^3-8x^2+6x-2-2x^3\left(a^2+1\right)a\)

\(\Leftrightarrow-2\left(xa-x+1\right)\left[\left(xa\right)^2+x^2a+2x^2-xa-2x+1\right]=0\)

\(\Leftrightarrow x.a-x+1=0\Leftrightarrow x\left(a-1\right)=-1\Leftrightarrow x=\dfrac{-1}{a-1}\)

\(\left(\sqrt{x\sqrt{3-2y}-\sqrt{x}}\right) ^2=x\sqrt{3-2y}-\sqrt{x}\)

\(=\dfrac{-a}{a-1}-\sqrt{\dfrac{-1}{a-1}}\)

\(\left(\sqrt{x\sqrt{3-2y}+2}+\sqrt{x+1}\right)=\sqrt{\dfrac{-a}{a-1}+2}+\sqrt{\dfrac{a-2}{a-1}}\)

\(\Rightarrow\left(\dfrac{-a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\left(\sqrt{\dfrac{-a}{a-1}+2}+\sqrt{\dfrac{a-2}{a-1}}\right)-4=0\)

\(\Leftrightarrow\left(-\dfrac{a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right).2\sqrt{\dfrac{a-2}{a-1}}=4\)

\(\Leftrightarrow\left(-\dfrac{a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\sqrt{\dfrac{a-2}{a-1}}=2\)

\(\Leftrightarrow\left(-1+\dfrac{-1}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\sqrt{1-\dfrac{1}{a-1}}=2\)(3)

\(đặt:1-\dfrac{1}{a-1}=u\Rightarrow\sqrt{-\dfrac{1}{a-1}}=\sqrt{u-1}\)

\(\left(3\right)\Leftrightarrow\left(u-2-\sqrt{u-1}\right)\sqrt{u}=2\)

bình phương lên tính được u

\(\Rightarrow u=.....\Rightarrow a\Rightarrow y=...\Rightarrow x=....\)

Với \(x=0\) không phải nghiệm

Với \(x>0\) chia 2 vế cho pt đầu cho \(x^3\)

\(\Rightarrow2-\dfrac{4}{x}+\dfrac{3}{x^2}-\dfrac{1}{x^3}=2\left(2-y\right)\sqrt{3-2y}\)

\(\Leftrightarrow1-\dfrac{1}{x}+\left(1-\dfrac{1}{x}\right)^3=\sqrt{3-2y}+\sqrt{\left(3-2y\right)^3}\)

Xét hàm \(f\left(t\right)=t+t^3\Rightarrow f'\left(t\right)=1+3t^2>0\Rightarrow f\left(t\right)\) đồng biến

\(\Rightarrow1-\dfrac{1}{x}=\sqrt{3-2y}\)

Thế vào pt dưới:

\(\left(\sqrt{x\left(1-\dfrac{1}{x}\right)-\sqrt{x}}\right)^2\left(\sqrt{x\left(1-\dfrac{1}{x}\right)+2}+\sqrt{x+1}\right)=4\)

\(\Leftrightarrow\left(x-\sqrt{x}-1\right)\left(\sqrt{x+1}+\sqrt{x+1}\right)=4\)

\(\Leftrightarrow\left(x-\sqrt{x}-1\right)\sqrt{x+1}=2\)

Phương trình này ko có nghiệm đẹp, chắc bạn ghi nhầm đề bài của pt dưới

a) Bất phương trình đã cho tương đương với hệ sau:

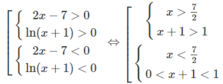
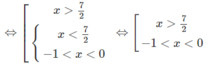
Vậy tập nghiệm là (−1;0) ∪ (7/2; + ∞ )

b) Tương tự câu a), tập nghiệm là (1/10; 5)

c) Đặt t = log 2 x , ta có bất phương trình 2 t 3  + 5 t 2  + t – 2 ≥ 0 hay (t + 2)(2 t 2  + t − 1) ≥ 0 có nghiệm −2 ≤ t ≤ −1 hoặc t ≥ 1/2

Suy ra 1/4 ≤ x ≤ 1/2 hoặc x ≥ 2

Vậy tập nghiệm của bất phương trình đã cho là: [1/4; 1/2] ∪ [ 2 ; + ∞ )

d) Bất phương trình đã cho tương đương với hệ:

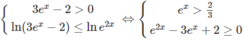
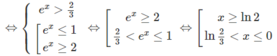
Vậy tập nghiệm là (ln(2/3); 0] ∪ [ln2; + ∞ )

1.

PT $\Leftrightarrow 2^{x^2-5x+6}+2^{1-x^2}-2^{7-5x}-1=0$

$\Leftrightarrow (2^{x^2-5x+6}-2^{7-5x})-(1-2^{1-x^2})=0$

$\Leftrightarrow 2^{7-5x}(2^{x^2-1}-1)-(2^{x^2-1}-1)2^{1-x^2}=0$

$\Leftrightarrow (2^{x^2-1}-1)(2^{7-5x}-2^{1-x^2})=0$

$\Rightarrow 2^{x^2-1}-1=0$ hoặc $2^{7-5x}-2^{1-x^2}=0$

Nếu $2^{x^2-1}=1\Leftrightarrow x^2-1=0$

$\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$

$2^{7-5x}-2^{1-x^2}=0$

$\Leftrightarrow 7-5x=1-x^2\Leftrightarrow x^2-5x+6=0$

$\Leftrightarrow (x-2)(x-3)=0\Leftrightarrow x=2; x=3$

2. Đặt $\sin ^2x=a$ thì $\cos ^2x=1-a$. PT trở thành:

$16^a+16^{1-a}=10$

$\Leftrightarrow 16^a+\frac{16}{16^a}=10$

$\Leftrightarrow (16^a)^2-10.16^a+16=0$

Đặt $16^a=x$ thì:

$x^2-10x+16=0$

$\Leftrightarrow (x-2)(x-8)=0$

$\Leftrightarrow x=2$ hoặc $x=8$

$\Leftrightarrow 16^a=2$ hoặc $16^a=8$

$\Leftrightarrow 2^{4a}=2$ hoặc $2^{4a}=2^3$

$\Leftrightarroww 4a=1$ hoặc $4a=3$

$\Leftrightarrow a=\frac{1}{4}$ hoặc $a=\frac{3}{4}$

Nếu $a=\frac{1}{4}\Leftrightarrow \sin ^2x=\frac{1}{4}$

$\Leftrightarrow \sin x=\pm \frac{1}{2}$

Nếu $a=\sin ^2x=\frac{3}{4}\Rightarrow \sin x=\pm \frac{\sqrt{3}}{2}$

Đến đây thì đơn giản rồi.