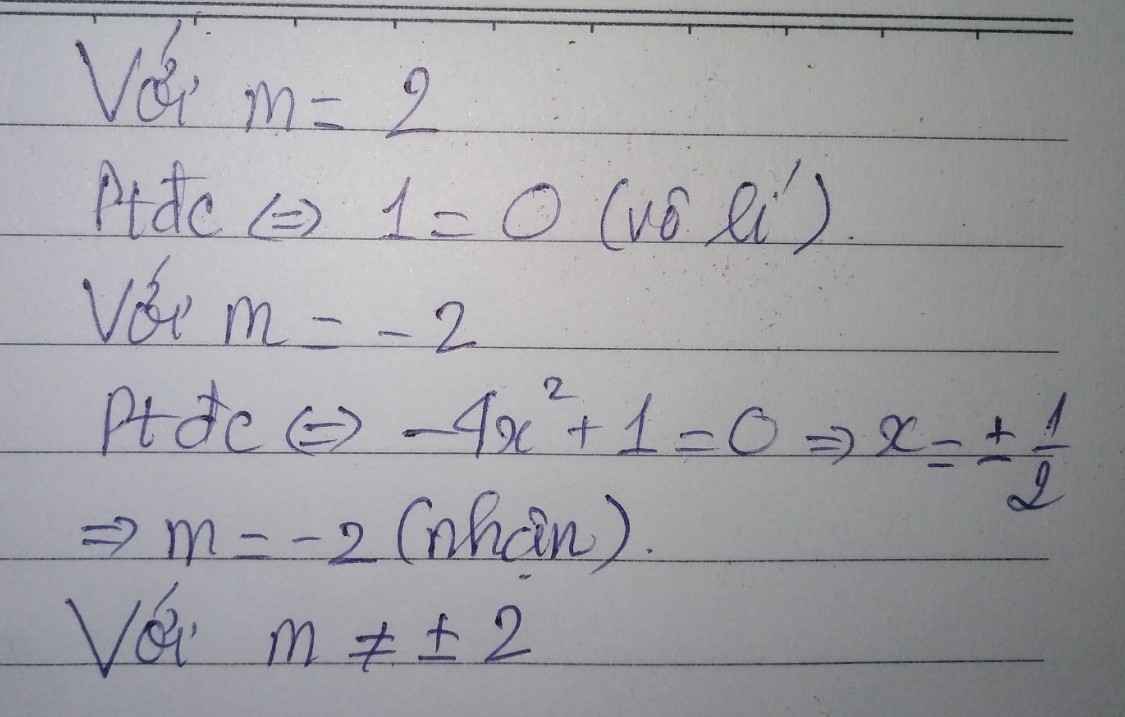x 4 − 5 x 3 + 8 x 2 − 10 x + 4 = 0 ⇔ ( x 4 + 4 x 2 + 4 ) − 5 x 3 + 4 x 2 − 10 x = 0

⇔ x 2 + 2 2 − 5 x 3 + 10 x + 4 x 2 = 0 ⇔ x 2 + 2 2 − 5 x x 2 + 2 + 4 x 2 = 0

Đặt t = x 2 + 2  ta được t 2 − 5 t x + 4 x 2 = 0 ⇔ t − x t − 4 x = 0

Hay phương trình đã cho ⇔ x 2 − x + 2 x 2 − 4 x + 2 = 0

⇔ x 2 − x + 2 = 0    ( V N ) x 2 − 4 x + 2 = 0 ⇔ x = 2 ± 2

Vậy phương trình không có nghiệm nguyên

Đáp án cần chọn là: D

\(\Leftrightarrow x^4+x-4x-4=0\)

=>x+1=0

hay x=-1

\(x^4-3x-4=0\\ x^4+x-4x-4=0\\ x^3\left(x+1\right)-4\left(x+1\right)=0\\ \left(x^3-4\right)\left(x+1\right)=0\)

\(\Rightarrow\left\{{}\begin{matrix}x^3-4=0\Leftrightarrow x^3=4\Leftrightarrow x=\sqrt[3]{4}\\x+1=0\Leftrightarrow x=-1\end{matrix}\right.\)

\(\Leftrightarrow\left(x^4+x^3-3x^2\right)-\left(x^3+x^2-3x\right)-\left(x^2+x-3\right)< 0\)

\(\Leftrightarrow x^2\left(x^2+x-3\right)-x\left(x^2+x-3\right)-1\left(x^2+x-3\right)< 0\)

\(\Leftrightarrow\left(x^2-x-1\right)\left(x^2+x-3\right)< 0\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1-\sqrt{13}}{2}< x< \dfrac{1-\sqrt{5}}{2}\\\dfrac{-1+\sqrt{13}}{2}< x< \dfrac{1+\sqrt{5}}{2}\end{matrix}\right.\)

đặt \(\hept{\begin{cases}\sqrt[3]{3x-2}=a\\\sqrt{6-5x}=b\ge0\end{cases}}\) ta sẽ có hệ sau \(\hept{\begin{cases}3a+4b=10\\5a^3+3b^2=8\end{cases}}\)

rút thế \(b=\frac{10-3a}{4}\)xuống phương trình dưới ta có\

\(5a^3+3\left(\frac{10-3a}{4}\right)^2=8\) hay 

\(80a^3+27a^2-180a+172=0\Leftrightarrow\left(a+2\right)\left(80a^2-133a+86\right)=0\Leftrightarrow a=-2\)

hay \(\sqrt[3]{3x-2}=-2\Leftrightarrow x=-2\) thay lại thỏa mãn

vậy phương trình có nghiệm duy nhất x=-2

Theo Vi-ét ta có:

△' = (m+1)² -m(m-2)

△' = 1 >0

Vậy pt luôn có nghiệm ∀m

@@

Đặt x2−2x+m=tx2−2x+m=t, phương trình trở thành t2−2t+m=xt2−2t+m=x

Ta có hệ {x2−2x+m=tt2−2t+m=x{x2−2x+m=tt2−2t+m=x

⇒(x−t)(x+t−1)=0⇒(x−t)(x+t−1)=0

⇔[x=tx=1−t⇔[x=tx=1−t

⇔[x=x2−2x+mx=1−x2+2x−m⇔[x=x2−2x+mx=1−x2+2x−m

⇔[m=−x2+3xm=−x2+x+1⇔[m=−x2+3xm=−x2+x+1

Phương trình hoành độ giao điểm của y=−x2+x+1y=−x2+x+1 và y=−x2+3xy=−x2+3x:

−x2+x+1=−x2+3x−x2+x+1=−x2+3x

⇔x=12⇒y=54⇔x=12⇒y=54

Đồ thị hàm số y=−x2+3xy=−x2+3x và y=−x2+x+1y=−x2+x+1: