Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Ta có: \(2x\left(x-3\right)+5\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
2) Ta có: \(\left(x^2-4\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)+\left(x-2\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3) Ta có: \(\left(2x-1\right)^2-\left(2x+5\right)^2=11\)
\(\Leftrightarrow4x^2-4x-1-4x^2-20x-25=11\)
\(\Leftrightarrow-24x=11+1+25=37\)
hay \(x=-\dfrac{37}{24}\)
5) Ta có: \(3x^2-5x-8=0\)
\(\Leftrightarrow3x^2+3x-8x-8=0\)
\(\Leftrightarrow3x\left(x+1\right)-8\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{8}{3}\end{matrix}\right.\)
8) Ta có: \(\left|x-5\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=3\\x-5=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=2\end{matrix}\right.\)
10) Ta có: \(\left|2x+1\right|=\left|x-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=x-1\\2x+1=1-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x=-1-1\\2x+x=1-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)

1, x(x-1)=2(x-1)
<=> x(x-1)-2(x-1)=0
<=> (x-2)(x-1)=0
<=>x=2 hoặc x=1
vậy ...
2, (x+2)(2x-3)=x^2 -4
<=>(x+2)(2x-3)=(x-2)(x+2)
<=> (x+2)(2x-3)-(x-2)(x+2)=0
<=> (x+2)(2x-3-x+2)=0
<=> x=-2 hoặc x=1
vây...
3,x^2 +3x +2=0
<=> x^2 +x+2x+2=0
<=>(x+2)(x+1)=0
<=> x=-2 hoặc x=-1
vậy ...
5, x^3+x^2-12x =0
<=> x(x^2+x-12)=0
<=>x(x^2-3x+4x-12)=0
<=>x(x+4)(x-3)=0
<=> x=0 hoặc x=-4 hoặc x=3
vậy ...

1: \(=6x^2+2x-15x-5-x^2+6x-9+4x^2+20x+25-27x^3-27x^2-9x-1\)
=-27x^3-18x^2+4x+10
2: =4x^2-1-6x^2-9x+4x+6-x^3+3x^2-3x+1+8x^3+36x^2+54x+27
=7x^3+37x^2+46x+33
5:
\(=25x^2-1-x^3-27-4x^2-16x-16-9x^2+24x-16+\left(2x-5\right)^3\)
\(=8x^3-60x^2+150-125+12x^2-x^3+8x-60\)
=7x^3-48x^2+8x-35

1)\(\left|1-5x\right|\)-1=3
\(\Leftrightarrow\)\(\left|1-5x\right|=4\)
Ta có: \(\left|1-5x\right|\)\(=1-5x\) khi \(1-5x\)\(\ge0\)\(\Leftrightarrow\)\(x\ge0\)
\(\left|1-5x\right|=-\left(1-5x\right)\) khi \(1-5x\)\(< \)\(0\)
+)Với \(x\ge0\) ta có:
\(1-5x=4\)
\(\Leftrightarrow\)\(1-4=5x\)
\(\Leftrightarrow\)\(-3=5x\)
\(\Leftrightarrow\)\(\dfrac{-3}{5}\)(ko t/m ĐK)
+)Với \(x\)<0 ta có:
-(1-5x)=4
\(\Leftrightarrow\)5x-1=4
\(\Leftrightarrow\)5x=5
\(\Leftrightarrow\)x=1(ko t/m ĐK)
Vậy pt vô nghiệm
3)\(\left|3x-4\right|=x-3\)
Ta có:\(\left|3x-4\right|=3x-4\)khi 3x-4\(\ge\)0\(\Leftrightarrow\)x\(\ge\)0
\(\left|3x-4\right|=-\left(3x-4\right)\) khi 3x-4<0\(\Leftrightarrow\)x<0
+)Với x\(\ge\)0 ta có:
\(\left|3x-4\right|=x-3\)
\(\Leftrightarrow\)3x-4=x-3
\(\Leftrightarrow\)3x-x=4-3
\(\Leftrightarrow\)2x=1
\(\Leftrightarrow\)\(\dfrac{1}{2}\)(t/m ĐK)
+) Với x<0 ta có:
\(\left|3x-4\right|=x-3\)
\(\Leftrightarrow\)-(3x-4)=x-3
\(\Leftrightarrow\)4-3x=x-3
\(\Leftrightarrow\)4+3=3x+x
\(\Leftrightarrow\)7=4x
\(\Leftrightarrow\)\(\dfrac{7}{4}\)(ko t/m ĐK)
Vậy nghiệm của pt là x=\(\dfrac{1}{2}\)
4)\(\left|2x-3\right|=3-2x\)
Ta có: \(\left|2x-3\right|=2x-3\) khi 2x-3\(\ge\)0\(\Leftrightarrow x\ge0\)
\(\left|2x-3\right|=-\left(2x-3\right)\) khi 2x-3<0\(\Leftrightarrow\)x<0
+)Với x\(\ge\)0 ta có:
\(\left|2x-3\right|=3-2x\)
\(\Leftrightarrow\)2x-3=3-2x
\(\Leftrightarrow\)2x+2x=3+3
\(\Leftrightarrow\)4x=6
\(\Leftrightarrow x=\)\(\dfrac{3}{2}\)(t/m ĐK)
+)Với x<0 ta có:
\(\left|2x-3\right|=3-2x\)
\(\Leftrightarrow\)-(2x-3)=3-2x
\(\Leftrightarrow\)3-2x=3-2x
\(\Leftrightarrow\)3-3=2x-2x
\(\Leftrightarrow\)0=0x(ko t/m ĐK)
Vậy nghiệm của pt là x=\(\dfrac{3}{2}\)
5)\(\left|x-3\right|+3x=7\)
\(\Leftrightarrow\)\(\left|x-3\right|=7-3x\)
Ta có:\(\left|x-3\right|=x-3\) khi x-3\(\ge\)0\(\Leftrightarrow\)x\(\ge\)0
\(\left|x-3\right|=-\left(x-3\right)\) khi x-3<0\(\Leftrightarrow\)x<0
+)Với x\(\ge\)0 ta có:
\(\left|x-3\right|=7-3x\)
\(\Leftrightarrow\)x-3=7-3x
\(\Leftrightarrow\)x+3x=3+7
\(\Leftrightarrow\)4x=10
\(\Leftrightarrow\)x=\(\dfrac{5}{2}\)(t/m ĐK)
+)Với x<0 ta có:
\(\left|x-3\right|=7-3x\)
\(\Leftrightarrow\)-(x-3)=7-3x
\(\Leftrightarrow\)3-x=7-3x
\(\Leftrightarrow\)3-7=x-3x
\(\Leftrightarrow\)-4=-2x
\(\Leftrightarrow\)x=2(ko t/m ĐK)
Vậy nghiệm của pt là x=\(\dfrac{5}{2}\)
1. \(\left|1-5x\right|-1=3\) (1)
* TH1 : 1-5x \(\ge\) 0 \(\Leftrightarrow\) 5x \(\le\) 1 \(\Leftrightarrow\) x \(\le\) \(\dfrac{1}{5}\)
Phương trình (1) \(\Leftrightarrow\) 1-5x -1 = 3
\(\Leftrightarrow\) -5x = 3
\(\Leftrightarrow\) x = \(\dfrac{-3}{5}\) ( thỏa mãn )
* TH2: 1-5x < 0 \(\Leftrightarrow\) 5x > 1 \(\Leftrightarrow\) x > \(\dfrac{1}{5}\)
Phương trình (1) \(\Leftrightarrow\) 5x -1 -1 = 3
\(\Leftrightarrow\) 5x = 5
\(\Leftrightarrow\) x = 1 ( thỏa mãn )
Vậy tập nghiệm của phương trình là S = \(\left\{\dfrac{-3}{5},1\right\}\)
3, \(\left|3x-4\right|=x-3\) (3)
* TH1 : 3x-4\(\ge\) 0 \(\Leftrightarrow\) 3x \(\ge\) 4 \(\Leftrightarrow\) x \(\ge\) \(\dfrac{4}{3}\)
Phương trình (3) \(\Leftrightarrow\) 3x-4 = x-3
\(\Leftrightarrow\) 2x = 1
\(\Leftrightarrow\) x = \(\dfrac{1}{2}\)(thỏa mãn )
* TH2 : 3x-4<0 \(\Leftrightarrow\)3x<4 \(\Leftrightarrow\) x < \(\dfrac{4}{3}\)
Phương trình (3) \(\Leftrightarrow\) -3x+4 = x-3
\(\Leftrightarrow\) -4x = -7
\(\Leftrightarrow\) x = \(\dfrac{7}{4}\) (loại)
Vậy tập nghiệm của phương trình là S= \(\left\{\dfrac{1}{2}\right\}\)

\(2.\left(x+3\right)\left(x+5\right)+\left(x+3\right)\left(3x-4\right)=0\\ \Leftrightarrow x^2+5x+3x+15+3x^2-4x+9x-12=0\\ \Leftrightarrow x^2+3x^2+5x+3x-4x+9x+15-12=0\\\Leftrightarrow 4x^2+13x+3=0\\\Leftrightarrow 4\left(x^2+\frac{13}{4}x+\frac{3}{4}\right)=0\\\Leftrightarrow x^2+\frac{13}{4}x+\frac{3}{4}=0\\ \Leftrightarrow x^2+\frac{1}{4}x+3x+\frac{3}{4}=0\\\Leftrightarrow x\left(x+\frac{1}{4}\right)+3\left(x+\frac{1}{4}\right)=0\\\Leftrightarrow \left(x+3\right)\left(x+\frac{1}{4}\right)=0\\\Leftrightarrow \left[{}\begin{matrix}x+3=0\\x+\frac{1}{4}=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-3\\x=-\frac{1}{4}\end{matrix}\right.\)
Vậy tập nghiệm của phương trình trên là: \(S=\left\{-3;-\frac{1}{4}\right\}\)
\(3.\left(x+6\right)\left(3x-1\right)+x+6=0\\ \Leftrightarrow3x^2-x+18x-6+x+6=0\\ \Leftrightarrow3x^2+18x=0\\ \Leftrightarrow3x\left(x+6\right)=0\\\Leftrightarrow \left[{}\begin{matrix}3x=0\\x+6=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)
Vậy tập nghiệm của phương trình trên là \(S=\left\{0;-6\right\}\)

a: \(\Leftrightarrow x^2-4-4x^2-4x-1-2x+3x^2=0\)
=>-6x-5=0
=>-6x=5
hay x=-5/6
b: \(\Leftrightarrow2x^3+8x^2+8x-8x^2-2x^3+16=0\)
=>8x+16=0
hay x=-2
c: \(\Leftrightarrow x^3-6x^2+12x-8+9x^2-1-x^3-3x^2-3x-1=0\)
=>9x-10=0
hay x=10/9
d: \(\Leftrightarrow10x-15-20x+28=19-2x^2-4x-2\)
\(\Leftrightarrow-10x+13+2x^2+4x-17=0\)
\(\Leftrightarrow2x^2-6x-4=0\)
\(\Leftrightarrow x^2-3x-2=0\)
\(\text{Δ}=\left(-3\right)^2-4\cdot1\cdot\left(-2\right)=9+8=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3-\sqrt{17}}{2}\\x_2=\dfrac{3+\sqrt{17}}{2}\end{matrix}\right.\)

\(1,\Leftrightarrow7-2x-4=-x-4\)
\(\Leftrightarrow x-2x=-4-7+4\)
\(\Leftrightarrow-x=-7\)
\(\Leftrightarrow x=7\)
Vậy \(S=\left\{7\right\}\)
\(2,\Leftrightarrow x-1-2x+1=9-x\)
\(\Leftrightarrow x+x-2x=9-1+1\)
\(\Leftrightarrow0x=9\)
\(\Rightarrow x\in\varnothing\)
Vậy \(S=\left\{\varnothing\right\}\)
\(3,\Leftrightarrow2x^2+3x-2x+3=2x^2+10x-x-5\)
\(\Leftrightarrow2x^2-2x^2+3x-2x-10x+x=-5-3\)
\(-8x=-8\)
\(\Rightarrow x=1\)
Vậy \(S=\left\{1\right\}\)

\(e,4\left(x-3\right)^2-\left(2x-1\right)\left(2x+1\right)=10\)
\(\Leftrightarrow4\left(x^2-6x+9\right)-\left(4x^2-1\right)=10\)
\(\Leftrightarrow4x^2-24x+36-4x^2+1=10\)
\(\Leftrightarrow-24x+37=10\)
\(\Leftrightarrow-24x=-27\)
\(\Leftrightarrow x=\dfrac{9}{8}\)
\(f,25\left(x+3\right)^2+ \left(1-5x\right)\left(1+5x\right)=8\)
\(\Leftrightarrow25\left(x^2+6x+9\right)+\left(1-25x^2\right)=8\)
\(\Leftrightarrow25x^2+150x+225+1-25x^2=8\)
\(\Leftrightarrow150x+226=8\)
\(\Leftrightarrow150x=-218\)
\(\Leftrightarrow x=-\dfrac{109}{75}\)
\(g,9\left(x+1\right)^2-\left(3x-2\right)\left(3x+2\right)=10\)
\(\Leftrightarrow9\left(x^2+2x+1\right)-\left(9x^2-4\right)=10\)
\(\Leftrightarrow9x^2+18x+9-9x^2+4=10\)
\(\Leftrightarrow18x+13=10\)
\(\Leftrightarrow18x=-3\)
\(\Leftrightarrow x=-\dfrac{1}{6}\)
\(h,-4\left(x-1\right)^2+\left(2x-1\right)\left(2x+1\right)=-3\)
\(\Leftrightarrow-4\left(x^2-2x+1\right)+\left(4x^2-1\right)=-3\)
\(\Leftrightarrow-4x^2+8x-4+4x^2-1=-3\)
\(\Leftrightarrow8x-5=-3\)
\(\Leftrightarrow8x=2\)
\(\Leftrightarrow x=\dfrac{1}{4}\)
#\(Toru\)
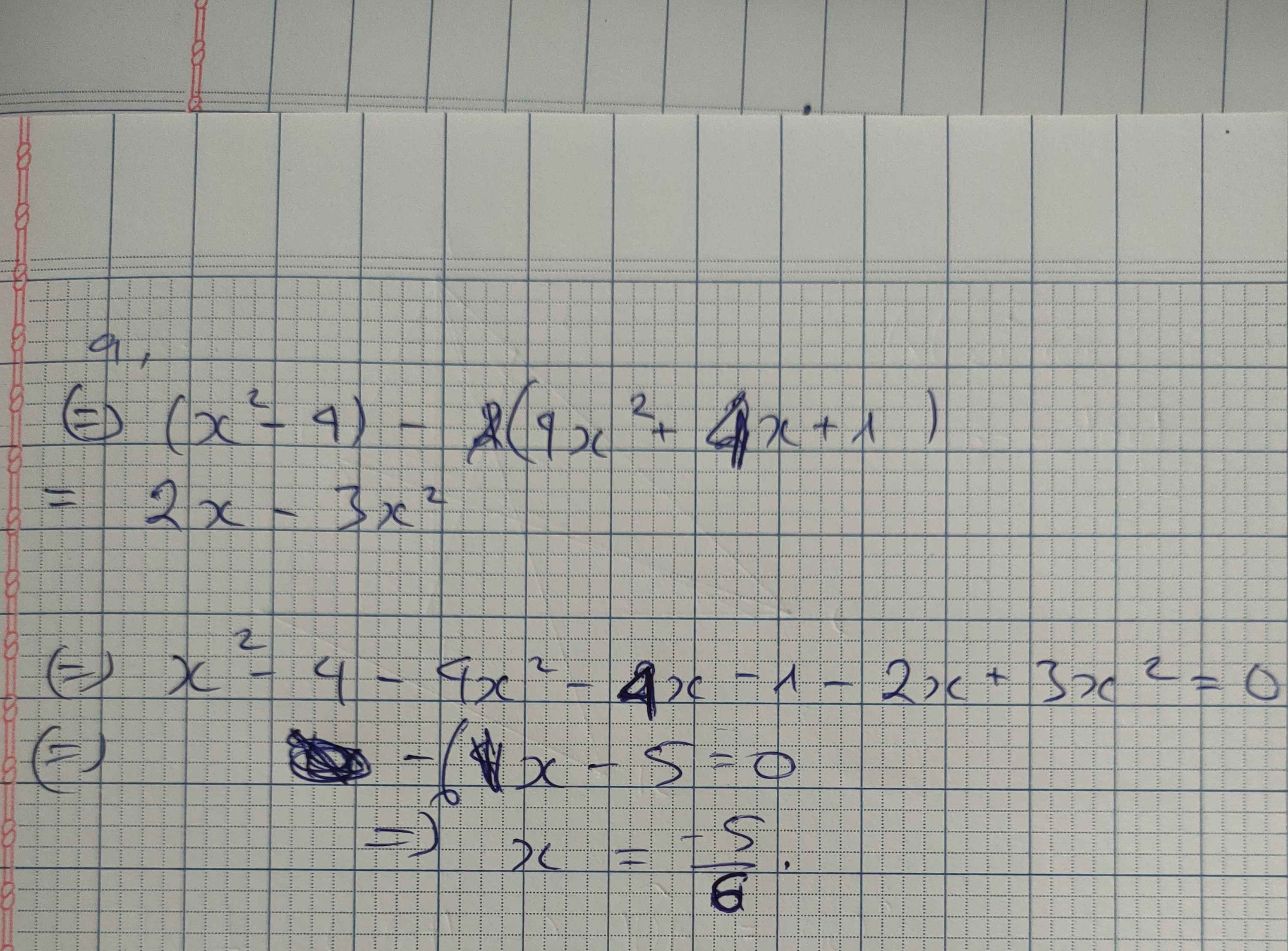
Giải mẫu 1 câu :
\(|1-5x|\)- 1 = 3
\(\Leftrightarrow\)\(|1-5x|\)= 4
TH1 : 1 - 5x = 4
\(\Leftrightarrow\)-5x = 5
\(\Leftrightarrow\)x = -1
TH2 : -1 + 5x = 4
\(\Leftrightarrow\)5x = 5
\(\Leftrightarrow\)x = 1
Vậy ...
Các câu khác tương tự !