
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(cos\left(4x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\Rightarrow cos\left(4x+\dfrac{\pi}{3}\right)=cos\dfrac{\pi}{6}\)
\(\Rightarrow\left[{}\begin{matrix}4x+\dfrac{\pi}{3}=\dfrac{\pi}{6}+k2\pi\\4x+\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
..... bạn tự tìm x nhé!
b)\(sin^2x-3sin3x+2=0\)\(\Rightarrow sin^2x-3\left(3sinx-4sin^3x\right)+2=0\)
\(\Rightarrow12sin^3x+sin^2x-9sinx+2=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\dfrac{2}{3}\\sinx=\dfrac{1}{4}\end{matrix}\right.\) \(\Rightarrow\).... bạn tự tìm x nhé!
c)\(tan\left(2x+10^o\right)=\sqrt{3}\Rightarrow tan\left(2x+10^o\right)=tan60^o\)
\(\Rightarrow2x+10^o=60^o+k180^o\)
\(\Rightarrow x=25^o+k90^o\left(k\in Z\right)\)
d) \(tanx\cdot cot2x=1\)
Đk: \(\left\{{}\begin{matrix}cosx\ne0\\sin2x\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+m\pi\\x\ne m\dfrac{\pi}{2}\end{matrix}\right.\)
Pt: \(\Rightarrow tanx=tan2x\Rightarrow x=2x+k\pi\)
\(\Rightarrow x=k\pi\)
Đối chiếu với đk trên thỏa mãn đk\(\Rightarrow x=k\pi\)

1.
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2}cos4x=\dfrac{1}{2}+\dfrac{1}{2}cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow-cos4x=cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow cos\left(4x-\pi\right)=cos\left(2x-\dfrac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-\pi=2x-\dfrac{\pi}{2}+k2\pi\\4x-\pi=\dfrac{\pi}{2}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{4}+\dfrac{k\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{3}\)
2.
\(\Leftrightarrow1-cos^2x+1-sin^24x=2\)
\(\Leftrightarrow cos^2x+sin^24x=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx=0\\sin4x=0\end{matrix}\right.\)
\(\Leftrightarrow cosx=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)

1.
\(sin\left(4x-10^0\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(4x-10^0\right)=sin45^0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-10^0=45^0+k360^0\\4x-10^0=135^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=55^0+k360^0\\4x=145^0+k360^0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=13,75^0+k90^0\\x=36,25^0+k90^0\end{matrix}\right.\) (\(k\in Z\))
2.
Đề không đúng
3.
ĐKXĐ: \(\left\{{}\begin{matrix}cos2x\ne0\\cosx\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(tan2x=tanx\)
\(\Rightarrow2x=x+k\pi\)
\(\Rightarrow x=k\pi\)
4.
\(cot\left(x+\dfrac{\pi}{5}\right)=-1\)
\(\Leftrightarrow x+\dfrac{\pi}{5}=-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{9\pi}{20}+k\pi\) (\(k\in Z\))

a, \(cos^2x-cosx=0\)
\(\Leftrightarrow cosx\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=0\end{matrix}\right.\)
b, \(2sin2x+\sqrt{2}sin4x=0\)
\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\1+\sqrt{2}cos2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\cos2x=-\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\2x=\dfrac{3\pi}{4}+k2\pi\\2x=\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{3\pi}{8}+k\pi\\x=\dfrac{\pi}{8}+k\pi\end{matrix}\right.\)
a, \(cos^2x-cosx=0\)
\(\Leftrightarrow cosx\left(cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=k2\pi\end{matrix}\right.\) (k ∈ Z)
Vậy...
b, \(2sin2x+\sqrt{2}sin4x=0\)
\(\Leftrightarrow2sin2x+2\sqrt{2}sin2x.cos2x=0\)
\(\Leftrightarrow2sin2x\left(1+\sqrt{2}cos2x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\cos2x=\dfrac{-\sqrt{2}}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x=k\pi\\2x=\pm\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\pm\dfrac{3\pi}{8}+k\pi\end{matrix}\right.\)
Vậy...
c, \(8cos^2x+2sinx-7=0\)
\(\Leftrightarrow8\left(1-sin^2x\right)+2sinx-7=0\)
\(\Leftrightarrow8sin^2x-2sinx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx=-\dfrac{1}{4}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\\x=arcsin\left(-\dfrac{1}{4}\right)+k2\pi\\x=\pi-arcsin\left(-\dfrac{1}{4}\right)+k2\pi\end{matrix}\right.\)
Vậy...
d, \(4cos^4x+cos^2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos^2x=\dfrac{3}{4}\\cos^2x=-1\left(loai\right)\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{cos2x+1}{2}=\dfrac{3}{4}\)
\(\Leftrightarrow cos2x=\dfrac{1}{2}\)
\(\Leftrightarrow2x=\pm\dfrac{\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+k\pi\)
Vậy...
e, \(\sqrt{3}tanx-6cotx+\left(2\sqrt{3}-3\right)=0\) (ĐK: \(x\ne\dfrac{k\pi}{2}\))
\(\Leftrightarrow\sqrt{3}tanx-\dfrac{6}{tanx}+\left(2\sqrt{3}-3\right)=0\)
\(\Leftrightarrow\sqrt{3}tan^2x+\left(2\sqrt{3}-3\right)tanx-6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=\sqrt{3}\\tanx=-2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k\pi\left(tm\right)\\x=arctan\left(-2\right)+k\pi\end{matrix}\right.\)
Vậy...

ĐKXĐ: ...
\(\Leftrightarrow sin^2x+3tanx=4sinxcosx-cos^2x\)
Chia 2 vế cho \(cos^2x\)
\(tan^2x+3tanx\left(1+tan^2x\right)=4tanx-1\)
\(\Leftrightarrow3tan^3x+tan^2x-tanx+1=0\)
\(\Leftrightarrow\left(tanx+1\right)\left(3tan^2x-2tanx+1\right)=0\)
\(\Leftrightarrow tanx=-1\)
\(\Leftrightarrow x=-\frac{\pi}{4}+k\pi\)

\(\sqrt{3}cosx+2sin^2\left(\dfrac{x}{2}-\pi\right)=1\)
\(\Leftrightarrow\sqrt{3}cosx+2sin^2\dfrac{x}{2}=1\)
\(\Leftrightarrow\sqrt{3}cosx-cosx=0\Leftrightarrow cosx=0\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\) ( k thuộc Z )
Vậy ...
22.
Nhận thấy \(cosx=0\) không phải nghiệm, chia 2 vế cho \(cos^2x\)
\(3tan^2x+2tanx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{1}{3}\right)+k\pi\end{matrix}\right.\)
Nghiệm dương nhỏ nhất của pt là: \(x=arctan\left(\dfrac{1}{3}\right)\)

\(y=\sin^4x+\cos^4x\\ =1-2\sin^2x\cdot\cos^2x\\ =1-\dfrac{1}{2}\sin^22x\\ 0\le\sin^22x\le1\\ \Leftrightarrow\dfrac{1}{2}\le y\le1\\ y_{min}=\dfrac{1}{2}\Leftrightarrow\sin^22x=1\Leftrightarrow x=\dfrac{k\pi}{2}\pm\dfrac{\pi}{4}\\ y_{max}=1\Leftrightarrow\sin^22x=0\Leftrightarrow x=k\pi\)
\(y=3\sin x+4\cos x\\ =5\left(\dfrac{3\sin x}{5}+\dfrac{4\cos x}{5}\right)\\ =5\cos\left(x-a\right),\forall\cos a=\dfrac{4}{5},\sin a=\dfrac{3}{5}\\ -1\le\cos\left(x-a\right)\le1\\ \Leftrightarrow-5\le y\le5\\ y_{min}=-5\Leftrightarrow\cos\left(x-a\right)=-1\\ y_{max}=5\Leftrightarrow\cos\left(x-a\right)=1\)

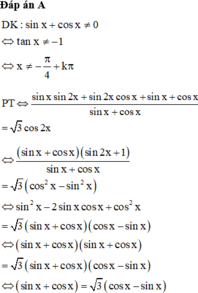
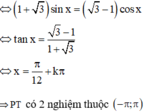
\(\sqrt{3}cos\left(2x-\dfrac{\pi}{4}\right)=-3\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{4}\right)=-\sqrt{3}< -1\)
Phương trình vô nghiệm