Đặt $x^2 = a > 0$ và $y^2 = b > 0$ thì hệ đã cho trở thành:

$\left\{\begin{aligned}&4a - 3b = 5\\&a + 2b = 4\\ \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&4a - 3b = 5\\&a = 4 - 2b\\ \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&16 - 8b - 3b = 5\\&a = 4 - 2b\\ \end{aligned}\right.$

$ \Leftrightarrow \left\{\begin{aligned}&- 11b = -11\\&a = 4 - 2b\\ \end{aligned}\right. \Leftrightarrow \left\{\begin{aligned}&b = 1 \, (tm)\\&a = 2 \, (tm)\\ \end{aligned}\right.$

Suy ra $x^2 = 2$ và $y^2 = 1$ từ đó em suy ra các nghiệm $(x;y)$ nhé

Đặt m =  x 2  – 2x

Ta có:  x 2 - 2 x 2  – 2 x 2  + 4x – 3 = 0

⇔  x 2 - 2 x 2  – 2( x 2  – 2x) – 3 = 0

⇔  m 2 – 2m – 3 = 0

Phương trình  m 2  – 2m – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0

Suy ra:  m 1  = -1,  m 2  = 3

Với m = -1 ta có:  x 2 – 2x = -1 ⇔  x 2  – 2x + 1 = 0

Phương trình  x 2  – 2x + 1 = 0 có hệ số a = 1, b = -2, c = 1 nên có dạng a + b + c = 0

Suy ra:  x 1 = x 2  = 1

Với m = 3 ta có:  x 2 – 2x = 3 ⇔  x 2 – 2x – 3 = 0

Phương trình  x 2  – 2x – 3 = 0 có hệ số a = 1, b = -2, c = -3 nên có dạng a – b + c = 0

Suy ra:  x 1  = -1,  x 2 = 3

Vậy phương trình đã cho có 3 nghiệm:  x 1  = 1,  x 2  = -1,  x 3  = 3

Đặt \(\dfrac{x}{\sqrt{4x-1}}=a\)

Theo đề, ta có phương trình:

a+1/a=2

\(\Leftrightarrow a+\dfrac{1}{a}=2\)

\(\Leftrightarrow\dfrac{a^2+1-2a}{a}=0\)

=>a=1

=>\(x=\sqrt{4x-1}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2=4x-1\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=3\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow x\in\left\{2+\sqrt{3};2-\sqrt{3}\right\}\)

Đặt m =4x -5

Ta có:  4 x - 5 2  – 6(4x -5) +8 =0 ⇔ m 2  -6m +8 =0

∆ ’ = - 3 2 -1.8 =9 -8=1 > 0

∆ ' = 1 = 1

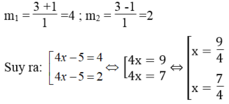
Vậy phương trình đã cho có 2 nghiệm x 1  =9/4 , x 2  =7/4

ĐK: \(x^3+4x^2+5x+6\ge0\)

Ta có: \(x^3+4x^2+5x+6=\left(x+3\right)\left(x^2+x+2\right);x^2+2x+5=\left(x+3\right)+\left(x^2+x+2\right)\)

Đặt \(\hept{\begin{cases}\sqrt{x+3}=u\\\sqrt{x^2+x+2}=v\end{cases}}\)

Vậy nên ta có phương trình: \(\)\(u^2+v^2=\frac{5}{2}uv\)

\(\Leftrightarrow2u^2-5uv+2v^2=0\Leftrightarrow\orbr{\begin{cases}u=2v\\u=\frac{1}{2}v\end{cases}}\)

Với u = 2v ta có: \(\sqrt{x+3}=2\sqrt{x^2+x+2}\Leftrightarrow x+3=4x^2+4x+8\)

\(\Leftrightarrow4x^2+3x+5=0\)   (Vô nghiệm)

Với \(u=\frac{1}{2}v\) ta có: \(2\sqrt{x+3}=\sqrt{x^2+x+2}\Leftrightarrow4x+12=x^2+x+2\)

\(\Leftrightarrow x^2-3x-10=0\Leftrightarrow\orbr{\begin{cases}x=5\\x=-2\end{cases}}\left(tmđk\right)\)

Vậy phương trình có nghiệm \(x\in\left\{5;-2\right\}\)

a) dat x-1=a

x=a+1

\(a+1+\sqrt{5+\sqrt{a}}=6\)

\(5-a=\sqrt{5+\sqrt{a}}\)

\(25-10a+a^2=5+\sqrt{a}\)

\(20-10a+a^2-\sqrt{a}=0\)

(a - \sqrt{5} - 5) (a + \sqrt{a} - 4) = 0

đúng nhưng b,c,d đâu