Ta có: \(8x^4-8x^3-4x^2+3x+1=0\)

\(\Leftrightarrow8x^3\left(x-1\right)-\left(4x^2-3x-1\right)=0\)

\(\Leftrightarrow8x^3\left(x-1\right)-\left(4x^2-4x+x-1\right)=0\)

\(\Leftrightarrow8x^3\left(x-1\right)-\left[4x\left(x-1\right)+\left(x-1\right)\right]=0\)

\(\Leftrightarrow8x^3\left(x-1\right)-\left(x-1\right)\left(4x+1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(8x^3-4x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(8x^3+4x^2-4x^2-2x-2x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left[4x^2\left(2x+1\right)-2x\left(2x+1\right)-\left(2x+1\right)\right]=0\)

\(\Leftrightarrow\left(x-1\right)\left(2x+1\right)\left(4x^2-2x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+1=0\\4x^2-2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\2x=-1\\\left(2x\right)^2-2\cdot2x\cdot\frac{1}{2}+\frac{1}{4}-\frac{5}{4}=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\frac{1}{2}\\\left(2x-\frac{1}{2}\right)^2=\frac{5}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\frac{1}{2}\\2x-\frac{1}{2}=\frac{\sqrt{5}}{2}\\2x-\frac{1}{2}=\frac{-\sqrt{5}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\frac{1}{2}\\2x=\frac{\sqrt{5}+1}{2}\\2x=\frac{1-\sqrt{5}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\frac{1}{2}\\x=\frac{\sqrt{5}+1}{4}\\x=\frac{1-\sqrt{5}}{4}\end{matrix}\right.\)

Vậy: \(S=\left\{1;-\frac{1}{2};\frac{\sqrt{5}+1}{4};\frac{1-\sqrt{5}}{4}\right\}\)

1.

\(x^4-6x^2-12x-8=0\)

\(\Leftrightarrow x^4-2x^2+1-4x^2-12x-9=0\)

\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-1=2x+3\\x^2-1=-2x-3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-4=0\\x^2+2x+2=0\end{matrix}\right.\)

\(\Leftrightarrow x=1\pm\sqrt{5}\)

3.

ĐK: \(x\ge-9\)

\(x^4-x^3-8x^2+9x-9+\left(x^2-x+1\right)\sqrt{x+9}=0\)

\(\Leftrightarrow\left(x^2-x+1\right)\left(\sqrt{x+9}+x^2-9\right)=0\)

\(\Leftrightarrow\sqrt{x+9}+x^2-9=0\left(1\right)\)

Đặt \(\sqrt{x+9}=t\left(t\ge0\right)\Rightarrow9=t^2-x\)

\(\left(1\right)\Leftrightarrow t+x^2+x-t^2=0\)

\(\Leftrightarrow\left(x+t\right)\left(x-t+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-t\\x=t-1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{x+9}\\x=\sqrt{x+9}-1\end{matrix}\right.\)

\(\Leftrightarrow...\)

ta có : \(x^4-4x^2+8x-4>0\Leftrightarrow\left(x^2-2x+2\right)\left(x^2+2x-2\right)>0\)

do \(x^2-2x+2>0\forall x\) rồi nên dấu của biểu thức phụ thuộc vào \(x^2+2x-2\) \(\Rightarrow\) bpt \(\Leftrightarrow x^2+2x-2>0\)

ta có : phương trình \(x^2+2x-2\) có 2 nghiệm \(\left[{}\begin{matrix}x=-1+\sqrt{3}\\x=-1-\sqrt{3}\end{matrix}\right.\)

và \(a=1>0\) \(\Rightarrow\) để \(x^2+2x-2>0\) thì \(\left[{}\begin{matrix}x>-1+\sqrt{3}\\x< -1-\sqrt{3}\end{matrix}\right.\)

vậy \(S=\left(-\infty;-1-\sqrt{3}\right)\cup\left(-1+\sqrt{3};+\infty\right)\)

Điều kiện : \(x\ge-1\)

Xét hàm số trên [\(-1;+\infty\) )  : \(f\left(x\right)=x^3-3x^2-8x+40\)

                                               \(g\left(x\right)=8\sqrt[4]{4x+4}\)

Theo bất đẳng thức Cauchy, ta có :

\(g\left(x\right)=\sqrt[4]{2^4.2^4.2^4\left(5x+4\right)}\le\frac{2^4+2^4+2^4+\left(4x+4\right)}{4}=x+13\)  (2)

Dấu bằng ở (2) xảy ra khi và chỉ khi x = 3

Mặt khác :

\(f\left(x\right)-\left(x+13\right)=x^3-3x^2-9x+27=\left(x-3\right)^2\left(x+3\right)\ge0\) với mọi \(x\ge-1\)  (3)

Dấu bằng ở (3) xảy ra khi và chỉ khi x = 3. Ta có :                

  \(\left(1\right)\Leftrightarrow f\left(x\right)=g\left(x\right)\) (4)

Vậy (4) có nghĩa là dấu bằng ở (2) và (3) đồng thời xảy ra,hay x = 3 (thỏa mãn điều kiện)

Phương trình đã cho có nghiệm duy nhất x = 3

a) \(2{x^2} + 3x + 1 \ge 0\)

Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x =  - 1,x = \frac{{ - 1}}{2}\)

hệ số \(a = 2 > 0\)

Ta có bảng xét dấu f(x) như sau:

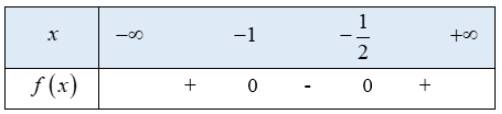
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le  - 1\\x \ge  - \frac{1}{2}\end{array} \right.\)

Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)

b) \( - 3{x^2} + x + 1 > 0\)

Tam thức bậc hai \(f\left( x \right) =  - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)

Hệ số \(a =  - 3 < 0\)

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)

Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)

c) \(4{x^2} + 4x + 1 \ge 0\)

Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)

hệ số \(a = 4 > 0\)

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)

Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)

d) \( - 16{x^2} + 8x - 1 < 0\)

Tam thức bậc hai \(f\left( x \right) =  - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)

hệ số \(a =  - 16 < 0\)

Ta có bảng xét dấu f(x) như sau:

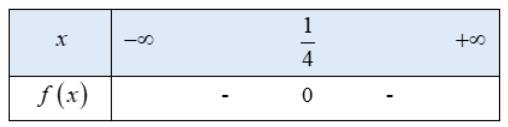
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)

Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)

e) \(2{x^2} + x + 3 < 0\)

Ta có \(\Delta  = {1^2} - 4.2.3 =  - 23 < 0\) và có \(a = 2 > 0\)

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)

Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)

g) \( - 3{x^2} + 4x - 5 < 0\)

Tam thức bậc hai \(f\left( x \right) =  - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) =  - 11 < 0\) và có \(a =  - 3 < 0\)

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)

Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)

a, Ta có : \(x^3-5x^2+8x-4=0\)

=> \(x^3-x^2-4x^2+4x+4x-4=0\)

=> \(x^2\left(x-1\right)-4x\left(x-1\right)+4\left(x-1\right)=0\)

=> \(\left(x-1\right)\left(x^2-4x+4\right)=0\)

=> \(\left(x-1\right)\left(x-2\right)^2=0\)

=> \(\left[{}\begin{matrix}x-1=0\\x-2=0\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

b, Ta có : \(x^4-4x^2+12x-9=0\)

=> \(x^4-x^3+x^3-x^2-3x^2+3x+9x-9=0\)

=> \(x^3\left(x-1\right)+x^2\left(x-1\right)-3x\left(x-1\right)+9\left(x-1\right)=0\)

=> \(\left(x-1\right)\left(x^3+3x^2-2x^2-6x+3x+9\right)=0\)

=> \(\left(x-1\right)\left(x^2\left(x+3\right)-2x\left(x+3\right)+3\left(x+3\right)\right)=0\)

=> \(\left(x-1\right)\left(x+3\right)\left(x^2-2x+3\right)=0\)

Mà \(x^2-2x+3=\left(x-1\right)^2+2>0\)

=> \(\left(x-1\right)\left(x+3\right)=0\)

=> \(\left[{}\begin{matrix}x-1=0\\x+3=0\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)

c, Ta có : \(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)-24=0\)

=> \(\left(x^2+x+4x+4\right)\left(x^2+2x+3x+6\right)-24=0\)

Đặt \(x^2+5x=a\) ta được phương trình :\(\left(a+4\right)\left(a+6\right)-24=0\)

=> \(a^2+4a+6a+24-24=0\)

=> \(a\left(a+10\right)=0\)

=> \(\left[{}\begin{matrix}a=0\\a+10=0\end{matrix}\right.\)

- Thay lại \(x^2+5x=a\) vào phương tình ta được :\(\left[{}\begin{matrix}x^2+5x=0\\x^2+5x+10=0\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}x\left(x+5\right)=0\\\left(x+\frac{5}{2}\right)^2+\frac{15}{4}=0\left(VL\right)\end{matrix}\right.\)

=> \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

( tự kết luận dùm mình nha )

a/ \(x^3-4x^2+4x-x^2+4x-4=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

b/ \(\Leftrightarrow x^4+2x^3-3x^2-2x^3-4x^2+6x+3x^2+6x-9=0\)

\(\Leftrightarrow x^2\left(x^2+2x-3\right)-2x\left(x^2+2x-3\right)+3\left(x^2+2x-3\right)=0\)

\(\Leftrightarrow\left(x^2+2x-3\right)\left(x^2-2x+3\right)=0\)

\(\Leftrightarrow x^2+2x-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)

c/ \(\Leftrightarrow\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)-24=0\)

\(\Leftrightarrow\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24=0\)

Đặt \(x^2+5x+4=t\)

\(t\left(t+2\right)-24=0\Leftrightarrow t^2+2t-24=0\Rightarrow\left[{}\begin{matrix}t=4\\t=-6\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x^2+5x+4=4\\x^2+5x+4=-6\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x^2+5x=0\\x^2+5x+10=0\left(vn\right)\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

a/ ĐKXĐ: \(x\ge4\)

Đặt \(\sqrt{x+4}+\sqrt{x-4}=a>0\)

\(\Rightarrow a^2=2x+2\sqrt{x^2-16}\)

Phương trình trở thành:

\(a=a^2-12\Leftrightarrow a^2-a-12=0\Rightarrow\left[{}\begin{matrix}a=4\\a=-3\left(l\right)\end{matrix}\right.\)

\(\Rightarrow\sqrt{x+4}+\sqrt{x-4}=4\)

\(\Leftrightarrow2x+2\sqrt{x^2-16}=16\)

\(\Leftrightarrow\sqrt{x^2-16}=8-x\left(x\le8\right)\)

\(\Leftrightarrow x^2-16=x^2-16x+64\)

\(\Rightarrow x=5\)

b/ \(x\ge-\frac{1}{2}\)

Đặt \(\left\{{}\begin{matrix}\sqrt{2x+1}=a\\\sqrt{4x^2-2x+1}=b\end{matrix}\right.\) ta được:

\(a+3b=3+ab\)

\(\Leftrightarrow ab-a-\left(3b-3\right)=0\)

\(\Leftrightarrow a\left(b-1\right)-3\left(b-1\right)=0\)

\(\Leftrightarrow\left(a-3\right)\left(b-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=3\\b=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x+1}=3\\\sqrt{4x^2-2x+1}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x+1=9\\4x^2-2x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=0\\x=\frac{1}{2}\end{matrix}\right.\)

Bài 2:

a/ \(\left\{{}\begin{matrix}\left(x+2y\right)^2-4xy-5=0\\4xy\left(x+2y\right)+5\left(x+2y\right)-1=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+2y\right)^2-\left(4xy+5\right)=0\\\left(4xy+5\right)\left(x+2y\right)-1=0\end{matrix}\right.\)

Đặt \(\left\{{}\begin{matrix}x+2y=a\\4xy+5=b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^2-b=0\\ab=1\end{matrix}\right.\) \(\Rightarrow a^2-\frac{1}{a}=0\Rightarrow a^3-1=0\)

\(\Rightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x+2y=1\\4xy+5=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1-2y\\4y\left(1-2y\right)+4=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=1-2y\\-8y^2+4y+4=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-1\\y=-\frac{1}{2}\Rightarrow x=2\end{matrix}\right.\)

b/Cộng vế với vế:

\(17x^2-2\left(4y^2+1\right)x+y^4+1=0\)

\(\Delta'=\left(4y^2+1\right)^2-17\left(y^4+1\right)=-y^4+8y^2-16\)

\(\Delta'=-\left(y^2-4\right)^2\ge0\Rightarrow y^2-4=0\Rightarrow\left[{}\begin{matrix}y=2\\y=-2\end{matrix}\right.\)

- Với \(y=2\) \(\Rightarrow x^2-2x+1=0\Rightarrow x=1\)

\(\)- Với \(y=-2\Rightarrow x^2-2x-7=0\Rightarrow x=1\pm2\sqrt{2}\)