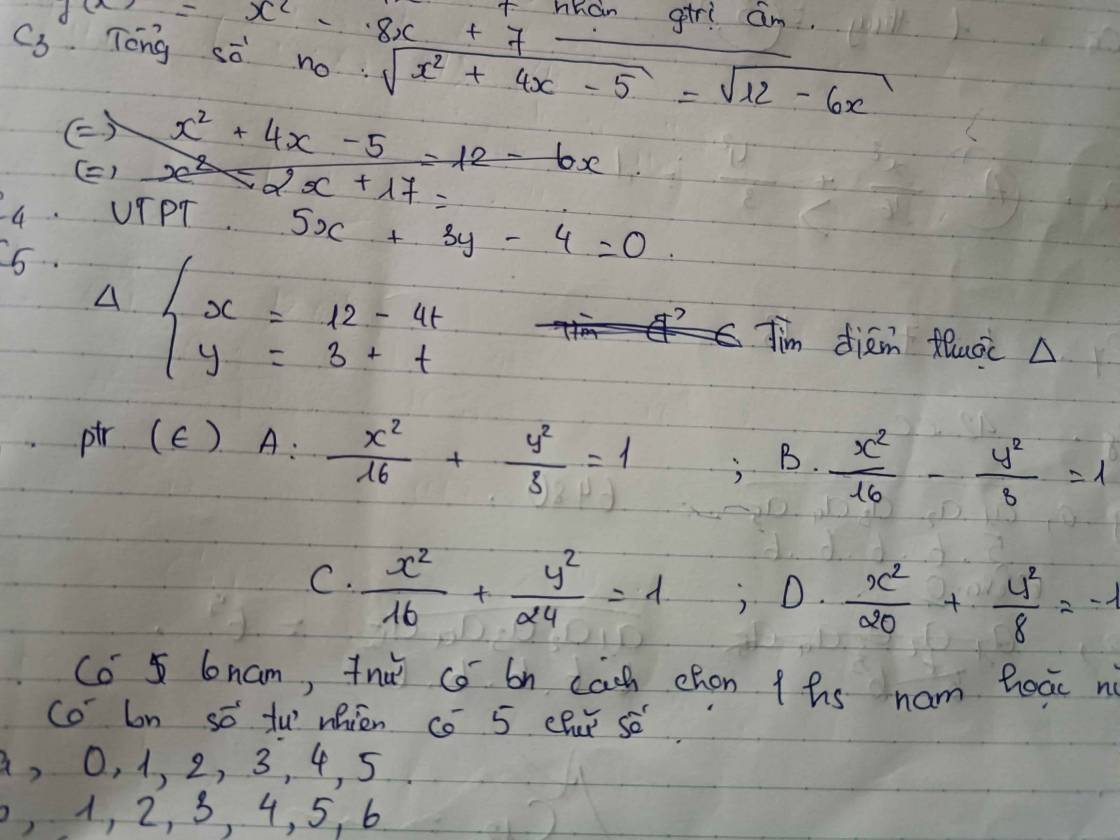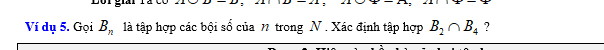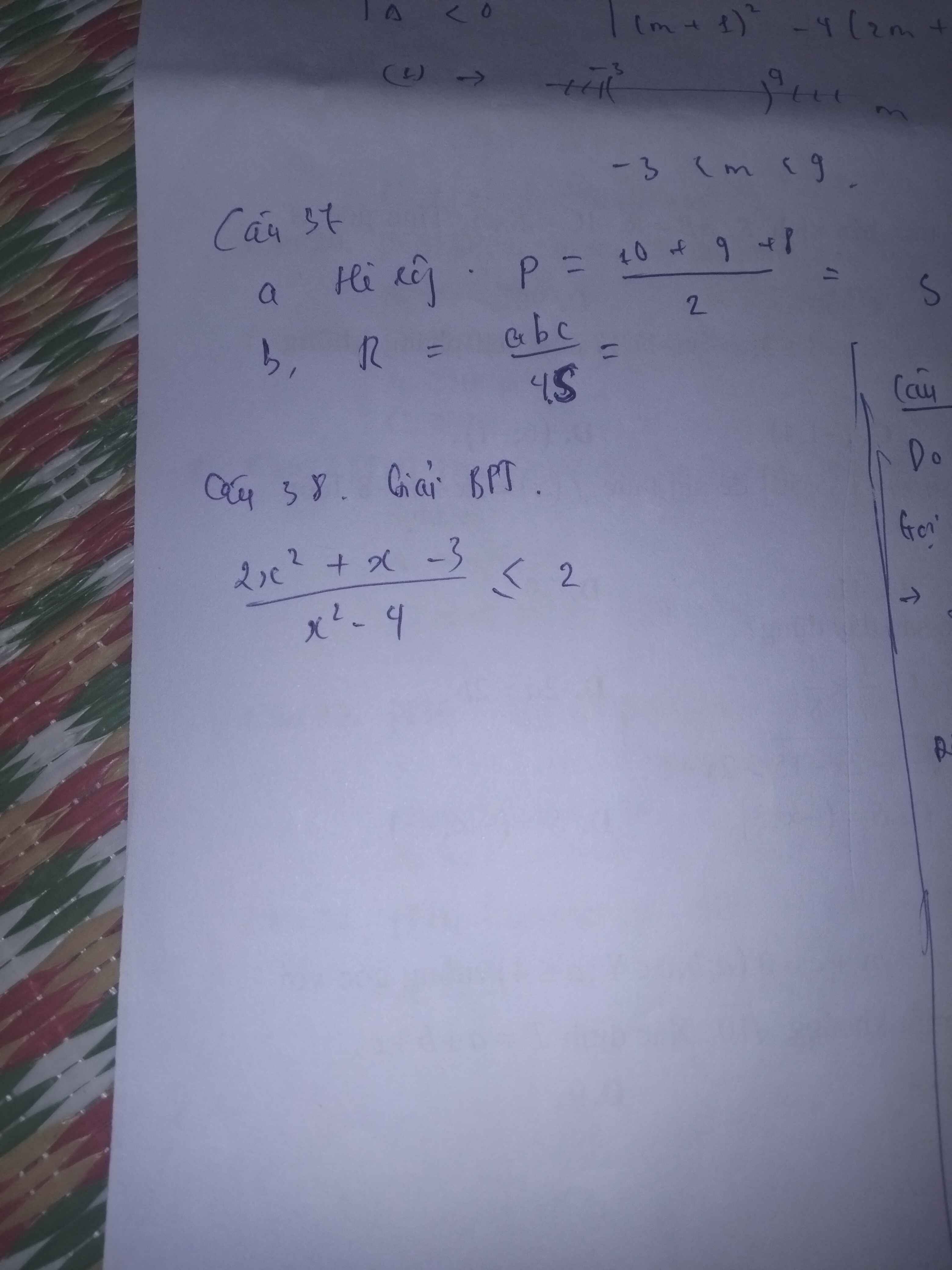\(B_2=\left\{x;x=2k,k\in N\right\}\)

\(B_4=\left\{x;x=4m,m\in N\right\}\)

Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)

\(\Rightarrow B_2\cap B_4=B_4\)

1: \(\Leftrightarrow x^2-6x=x^2-7x+10\)

hay x=10

sao câu 1 hoài v ạ.Còn câu 2,3 nữa á.

Câu 5: 

\(\Leftrightarrow-x^2+7x-9+2x-9=0\)

\(\Leftrightarrow x^2-9x+18=0\)

=>x=3

=>Chọn A

Không biết nãy bị lỗi ở đâu, mình gửi lại:<

1: \(\Leftrightarrow x^2-6x=x^2-7x+10\)

hay x=10

a) \(d\left(A;\Delta\right)=\dfrac{\left|4.1-3.3+2\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{3}{5}\)

b) \(\overrightarrow{AB}=\left(-3;-2\right)\) là VTCP của đường thẳng d

PT tham số của d: \(\left\{{}\begin{matrix}x=1-3t\\y=3-2t\end{matrix}\right.\left(t\in R\right)\)

c) Đường tròn (C) có bán kính \(R=AB=\sqrt{\left(1+2\right)^2+\left(3-1\right)^2}=\sqrt{13}\)

PT đường tròn (C): \(\left(x-1\right)^2+\left(y-3\right)^2=13\)

\(\dfrac{2x^2+x-3}{x^2-4}-2\le0\Leftrightarrow\dfrac{x+5}{x^2-4}\le0\)

\(\Leftrightarrow\dfrac{x+5}{\left(x-2\right)\left(x+2\right)}\le0\)

Bảng xét dấu:

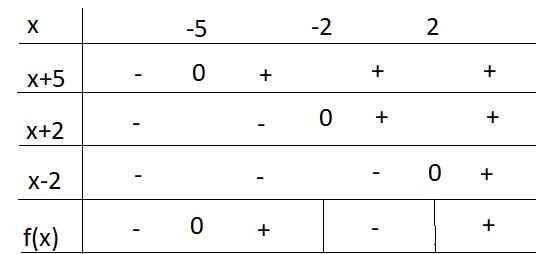
Từ bảng xét dấu ta được nghiệm của BPT là:

\(\left[{}\begin{matrix}x\le-5\\-2< x< 2\end{matrix}\right.\)

1.