Chọn B.

Phương pháp:

+) Tính số phần tử của không gian mẫu.

+) Gọi A là biến cố: "Hiệu số chấm xuất hiện trên các mặt của hai con súc sắc bằng 2". Tìm đẩy đủ các bộ số có hiệu bằng 2.

+) Tính xác suất của biến cố A.

Cách giải:

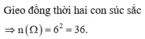
Gọi A là biến cố: "Hiệu số chấm xuất hiện trên các mặt của hai con súc sắc bằng 2".

Các bộ số có hiệu bằng 2 là (1;3); (2;4); (3;5); (4;6) 

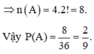
Đáp án A

Tổng số chấm trên mặt xuất hiện trong hai lần gieo ≥ 11  khi các kết quả là 6 ; 6 , 5 ; 6 , 6 ; 5  

Gọi x là xác suất xuất hiện mặt 6 chấm suy ra x 2  là xác suất xuất hiện các mặt còn lại

Ta có 5. x 2 + x = 1 ⇒ x = 2 7 .  

Do đó xác suất cần tìm là  2 7 2 + 2 7 . 1 7 + 1 7 . 2 7 = 8 49

Đáp án là B

Vì với mọi trường hợp khi đếm số chấm con xúc sắc thứ nhất, có đúng một trường hợp trên sáu trường hợp để con xúc sắc thứ hai cộng vào có tổng là 7 (Ví dụ xúc sắc đầu là 1 thì xúc sắc 2 phải là 6, xúc sắc một là hai thì xúc sắc 2 là 5…)

Số phần tử của không gian mẫu là: n Ω = 6 2 = 36  

Gọi A: “tổng số chấm trên mặt xuất hiện của hai con súc sắc đó không vượt quá 5”

Chọn: C

Đáp án là A

Số phần tử không gian mẫu n Ω = 36

Gọi biến cố  " Số chấm xuất hiện trên mặt của hai con súc sắc là số chẳn".

Ta có các khả năng xảy ra:  

2 ; 2 ; 2 ; 4 ; 2 ; 6 ; 4 ; 4 ; 4 ; 6 ; 6 ; 6 ; 4 ; 2 ; 6 ; 2 ; 6 ; 4 ⇒ n A = 9

Xác suất cần tính:  P A = 1 4

Đáp án C

Có 6 khả năng xảy ra khi tung súc sắc nên số phần tử của không gian mẫu là n ( Ω ) = 6 .

Gọi A là biến cố: Phương trình x 2 + b x + 2 = 0  (1) có hai nghiệm phân biệt.

Phương trình (1) có hai nghiệm phân biệt ⇔ b 2 − 8 > 0 ⇔ b ∈ 3 ; 4 ; 5 ; 6 ⇒ n A = 4 .

Vậy xác suất cần tính là p A = 2 3 .

Đáp án D

Đáp án C

Số phần tử không gian mẫu là 6 3 = 216.  

Các bộ ba số lập thành một cấp số cộng là ( 1 , 2 , 3 ) ,   ( 2 , 3 , 4 ) ,   ( 3 , 4 , 5 ) ,  ​ ( 4 , 5 , 6 )  . Bốn trường hợp trên với các hoán vị sẽ có 4 ⋅ 6  .

Xác suất cần tìm là 24 216 = 1 9 .  

Đáp án A.

Ta thấy phương trình x 2 - b x + b - 1 = 0  có a + b + c = 0  nên có nghiệm x 1 = 1 , x 2 = b - 1 .

Vậy để phương trình có nghiệm lớn hơn 3 thì b - 1 > 3 ⇔ b > 4 ⇒ b ∈ 5 ; 6 .

Do đó xác suất để phương trình có nghiệm lớn hơn 3 là 2 6 = 1 3 . Ta chọn A.