
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 7:
Xét hình bình hành ABCD, gọi O là giao của AC và BD
\(OB=OD=\dfrac{BD}{2}\Rightarrow BD=2OB\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
\(BN=\dfrac{1}{3}BD\left(gt\right)\Rightarrow BN=\dfrac{1}{3}.2OB=\dfrac{2}{3}OB\)
Xét hbh ABEF, gọi I là giao của AE và BF ta có
\(IA=IE=\dfrac{AE}{2}\Rightarrow AE=2IA\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
\(AM=\dfrac{1}{3}AE\left(gt\right)\Rightarrow AM=\dfrac{1}{3}.2IA=\dfrac{2}{3}IA\) (1)
Xét tg ABF có
\(IB=IF\) (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => IA là trung tuyến của tg ABF (2)
Từ (1) và (2) => M là trọng tâm của tg ABF
Gọi K là giao của BM với AF => BK là trung tuyến của tg ABF
\(\Rightarrow BM=\dfrac{2}{3}BK\)
Xét tg BOK có
\(BN=\dfrac{2}{3}OB\left(cmt\right)\Rightarrow\dfrac{BN}{OB}=\dfrac{2}{3}\)
\(BM=\dfrac{2}{3}BK\left(cmt\right)\Rightarrow\dfrac{BM}{BK}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{BN}{OB}=\dfrac{BM}{BK}=\dfrac{2}{3}\) => MN//OK (Talet đảo trong tam giác) (3)
Xét tg ACF có
BK là trung tuyến của tg ABF (cmt) => KA=KF
Ta có
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> OK là đường trung bình của tg ACF => OK//CF (4)
Từ (3) và (4) => MN//CF
mà \(CF\in\left(DCEF\right)\)
=> MN//(DCEF)

a.
Kẻ \(AE\perp SD\)
Do \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp AE\)
\(\Rightarrow AE\perp\left(SCD\right)\Rightarrow AE=d\left(A;\left(SCD\right)\right)\)
\(AE=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\dfrac{4a\sqrt[]{5}}{5}\)
\(\left\{{}\begin{matrix}AM\cap\left(SCD\right)=C\\MC=\dfrac{3}{4}AC\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SCD\right)\right)=\dfrac{3}{4}d\left(A;\left(SCD\right)\right)=\dfrac{3a\sqrt{5}}{5}\)
\(\left\{{}\begin{matrix}MN\cap\left(SCD\right)=S\\NS=\dfrac{1}{2}MS\end{matrix}\right.\) \(\Rightarrow d\left(N;\left(SCD\right)\right)=\dfrac{1}{2}d\left(M;\left(SCD\right)\right)=\dfrac{3a\sqrt{5}}{6}\)
b.
Qua S kẻ tia Sx song song cùng chiều tia DC, trên Sx lấy F sao cho \(SF=DC\)
\(\Rightarrow CDSF\) là hình bình hành \(\Rightarrow CF||SD\Rightarrow\left(SAD\right)||\left(BCF\right)\Rightarrow CD\perp\left(BCF\right)\)
Qua B kẻ \(BG\perp CF\Rightarrow BG\perp\left(SCD\right)\Rightarrow\widehat{BDG}\) là góc giữa BD và (SCD)
SF song song và bằng CD nên SF song song và bằng AB \(\Rightarrow SABF\) là hbh
\(\Rightarrow FB||SA\Rightarrow FB\perp\left(ABCD\right)\) \(\Rightarrow FB\perp BC\)
\(BF=SA=2a\Rightarrow BG=\dfrac{BF.BC}{\sqrt{BF^2+BC^2}}=\dfrac{4a\sqrt{5}}{5}\)
\(BD=\sqrt{AB^2+AD^2}=5a\)
\(\Rightarrow sin\widehat{BDG}=\dfrac{BG}{BD}=\dfrac{4\sqrt{5}}{25}\)
c.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow\widehat{DBA}\) là góc giữa BD và (SAB)
\(tan\widehat{DBA}=\dfrac{AD}{AB}=\dfrac{4}{3}\Rightarrow\widehat{DBA}\)
d.
Từ B kẻ \(BH\perp AC\) (H thuộc AC)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BH\)
\(\Rightarrow BH\perp\left(SAC\right)\Rightarrow\widehat{BSH}\) là góc giữa SB và (SAC)
\(BH=\dfrac{AB.BC}{\sqrt{AB^2+BC^2}}=\dfrac{12a}{5}\)
\(\Rightarrow sin\widehat{BSH}=\dfrac{BH}{SB}=\dfrac{12\sqrt{13}}{65}\Rightarrow\widehat{BSH}\)


MN là đường trung bình tam giác SAB \(\Rightarrow\) MN song song và bằng 1 nửa AB
Gọi P là trung điểm AD \(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow P\in\left(MNQ\right)\)
\(\Rightarrow\) MNQP là thiết diện của chóp và (MNQ)
Do MN song song PQ \(\Rightarrow\) MNQP là hình thang
Lại có M, P là trung điểm SA, AD \(\Rightarrow MP=\dfrac{1}{2}SD\)
Tương tự \(NQ=\dfrac{1}{2}SC\Rightarrow MP=NQ=\dfrac{b\sqrt{3}}{2}\)
\(\Rightarrow\) Thiết diện là hình thang cân
\(PQ=AB=a\) ; \(MN=\dfrac{1}{2}PQ=\dfrac{a}{2}\)
Kẻ \(MH\perp PQ\Rightarrow PH=\dfrac{PQ-MN}{2}=\dfrac{a}{4}\)
\(\Rightarrow MH=\sqrt{MP^2-PH^2}=\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)
\(S=\dfrac{1}{2}\left(MN+PQ\right).MH=\dfrac{3a}{4}.\sqrt{\dfrac{3b^2}{4}-\dfrac{a^2}{16}}\)

\(\Leftrightarrow-4sinx.cosx\left(cos^2x-sin^2x\right)-\sqrt{3}cos4x+1=0\)
\(\Leftrightarrow-2sin2x.cos2x-\sqrt{3}cos4x+1=0\)
\(\Leftrightarrow-sin2x-\sqrt{3}cos2x+1=0\)
\(\Leftrightarrow\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}cos2x=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\2x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=-\dfrac{\pi}{12}+k\pi\end{matrix}\right.\)

6. Trên \(\left[0;\dfrac{\pi}{2}\right]\) hàm \(y=cosx\) giảm còn \(y=sinx\) tăng
\(\Rightarrow\dfrac{1+cosx}{1+sinx}\) giảm
\(\Rightarrow y_{max}=y\left(0\right)=2\)
\(y_{min}=y\left(\dfrac{\pi}{2}\right)=\dfrac{1}{2}\)
7. Hàm không tồn tại GTLN trên khoảng đã cho (x càng gần \(-\dfrac{\pi}{4}\) thì y càng gần dương vô cực)
\(1+tanx\) tăng, không âm \(\Rightarrow\dfrac{1}{1+tanx}\) giảm \(\Rightarrow y_{min}=y\left(\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)

3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
 Giú em tính giới hạn với ạ. Cần gấp gấp ạ
Giú em tính giới hạn với ạ. Cần gấp gấp ạ Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ
Giúp em với ạ. Cần rất gấp ạ. Em cảm ơn ạ





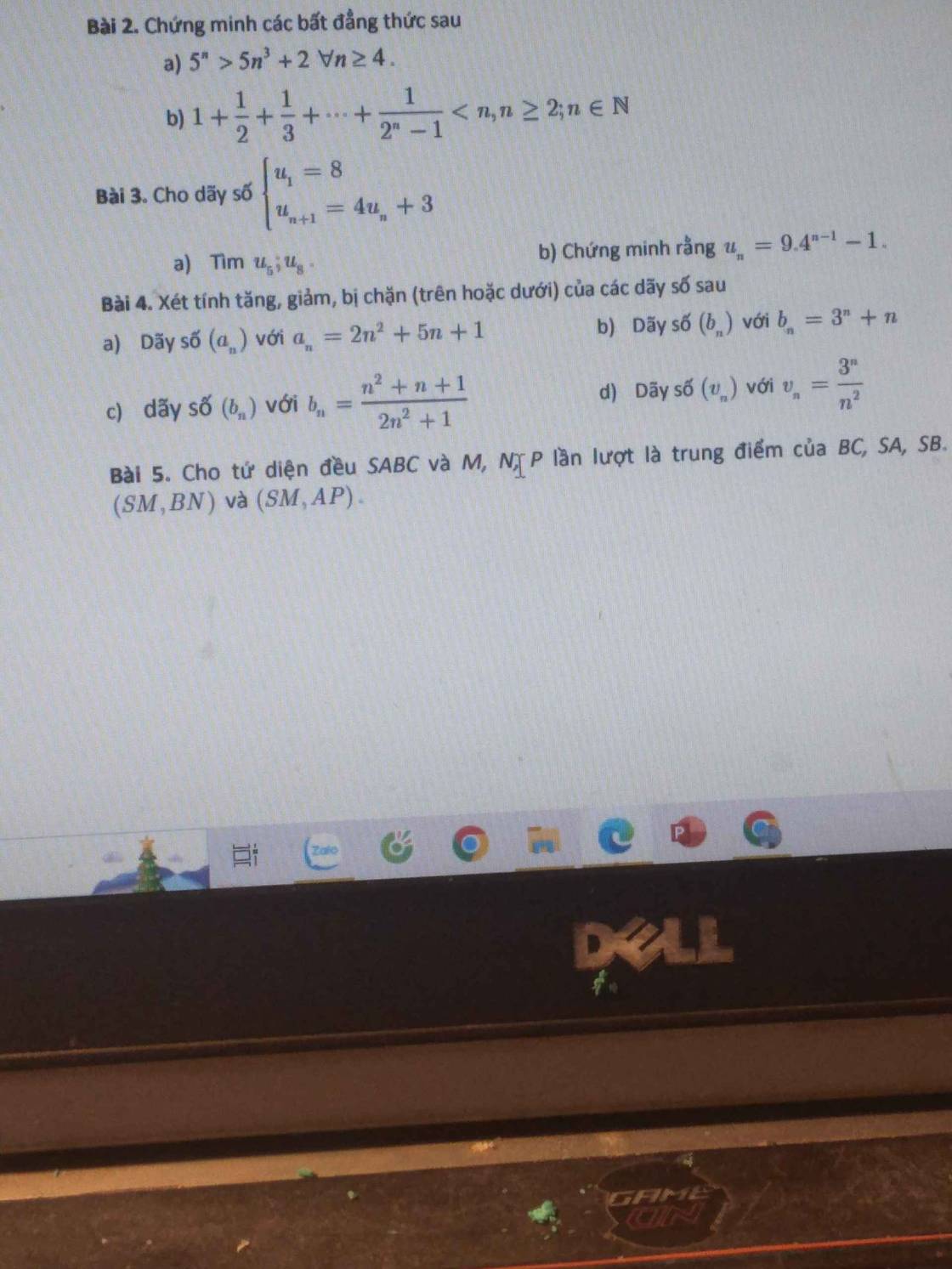 giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ


\(=lim_{x\rightarrow0}\left(\dfrac{5\cdot x\cdot\left(4x+2\right)}{5\cdot sin5x\cdot\left(\sqrt{4x^2+2x+1}+1\right)}-\dfrac{5\cdot x}{5\cdot sin5x\cdot\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}\right)\)\(lim_{x\rightarrow0}\dfrac{\sqrt{4x^2+2x+1}-\sqrt[3]{x+1}}{sin5x}=lim_{x\rightarrow0}(\dfrac{\sqrt{4x^2+2x+1}-1}{sin5x}-\dfrac{\sqrt[3]{x+1}-1}{sin5x})\)\(=lim_{x\rightarrow0}\left(\dfrac{1}{\dfrac{sin5x}{5x}}\cdot\left(\dfrac{4x+2}{(\sqrt{4x^2+2x+1}+1)\cdot5}-\dfrac{1}{5\cdot\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}\right)\right)\)(1)
chú ý : \(lim _{x\rightarrow0}\dfrac{1}{\dfrac{sin5x}{5x}}=\dfrac{1}{5}\)
Hay (1)= \(\dfrac{1}{5}\cdot\left(\dfrac{2}{2\cdot5}-\dfrac{1}{5\cdot3}\right)=\dfrac{2}{75}\)