K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
Khoảng cách giữa 2 địa điểm: $PQ=40$ cm
Độ cao đầu băng chuyền 1: $MP=15$ cm
Độ cao đầu băng chuyền còn lại: $RQ=6$ cm
Độ dài băng chuyền: $MP$
Kẻ $RN\perp MP$. Dễ thấy $NRQP$ là hình chữ nhật nên $NR=PQ=40$ (cm)
$MN=MP-RQ=15-6=9$ (cm)
Độ dài băng chuyền: $MR=\sqrt{NM^2+NR^2}=\sqrt{9^2+40^2}=41$ (cm)
---------
b. Bạn không cho biết $B,H,A,C$ là những điểm nào?
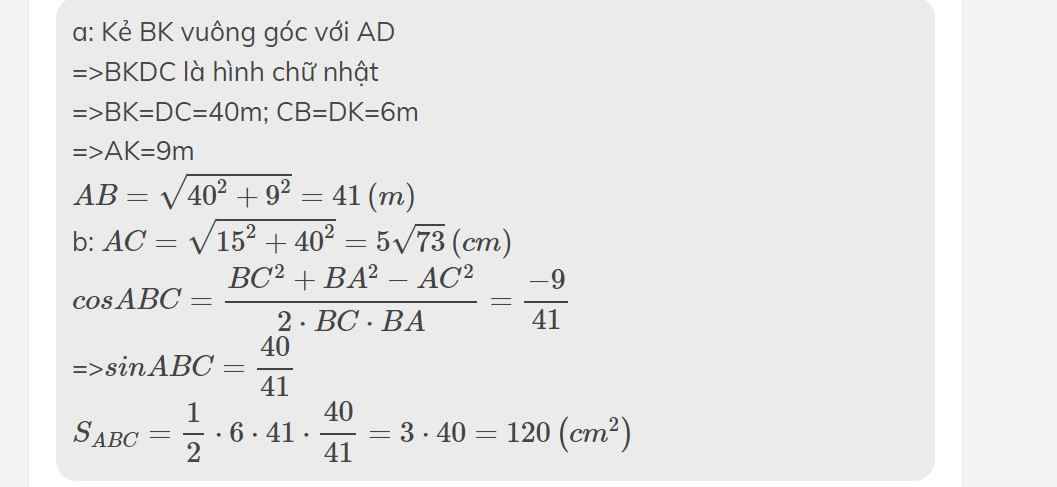
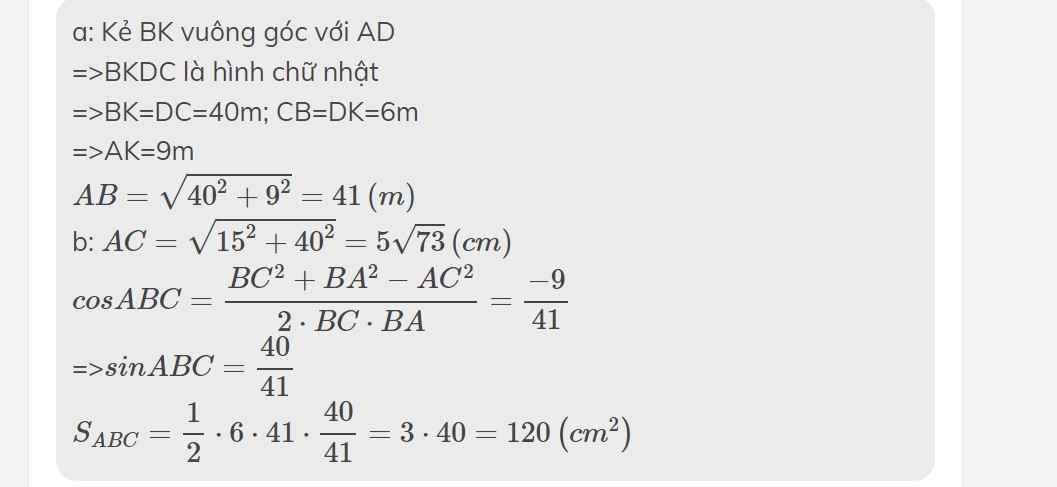
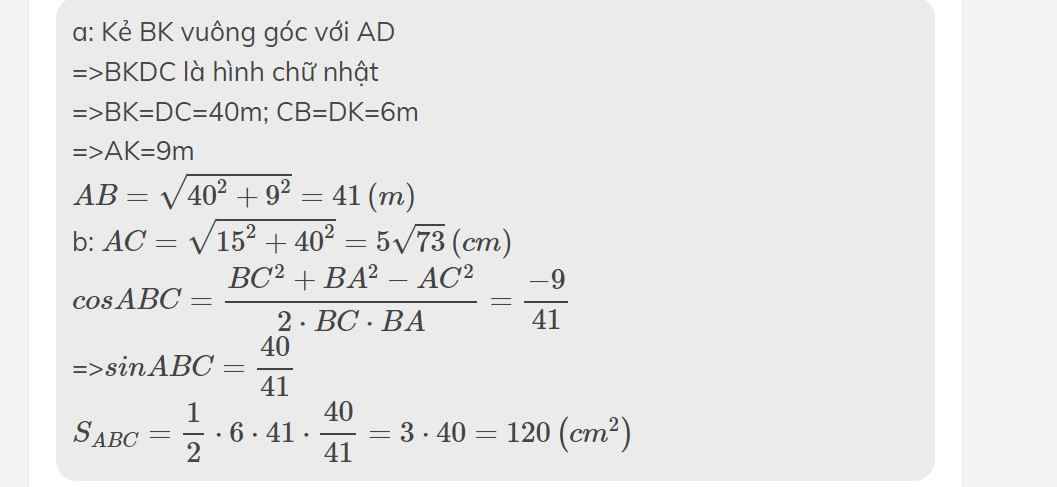
a: Kẻ BK vuông góc với AD
=>BKDC là hình chữ nhật
=>BK=DC=40m; CB=DK=6m
=>AK=9m
\(AB=\sqrt{40^2+9^2}=41\left(m\right)\)
b: \(AC=\sqrt{15^2+40^2}=5\sqrt{73}\left(cm\right)\)
\(cosABC=\dfrac{BC^2+BA^2-AC^2}{2\cdot BC\cdot BA}=\dfrac{-9}{41}\)
=>\(sinABC=\dfrac{40}{41}\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot41\cdot\dfrac{40}{41}=3\cdot40=120\left(cm^2\right)\)