Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có: AM=BM(gt)
AN=CN(gt)
=>PQ là đường trung bình của ht BMNC
=>PQ//MN
Bên dưới giải thiếu
Xét ΔABC có:
AM=BM(gt)
AN=CN(gt)
=>MN là đường trung bình
=>MN//BC
=>BMNC là hình thnag
(Xong nối đoạn dưới vào)

a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
=>OA/OC=OB/OD=AB/CD
=>OA/10=OC/18=(OA+OC)/(10+18)=21/28=3/4
=>OA=7,5cm; OC=13,5cm
b: OA/OC=OB/OD
=>OA*OD=OB*OC
c: AM/CN=AB/CD=OA/OC
Xét ΔOAM và ΔOCN có
OA/OC=AM/CN
góc OAM=góc OCN
=>ΔOAM đồng dạng với ΔOCN
=>góc AOM=góc CON
=>góc AOM+góc AON=180 độ
=>M,O,N thẳng hàng

Ta có: (AB+DC):2 = MN ( đường trung bình của hình thang)
=> AB+DC = MN.2 = 3.2 =6
AB = 6 - DC = 6 - 4 =2
=> AB=2

Lời giải:
Khoảng cách giữa 2 địa điểm: $PQ=40$ cm
Độ cao đầu băng chuyền 1: $MP=15$ cm
Độ cao đầu băng chuyền còn lại: $RQ=6$ cm
Độ dài băng chuyền: $MP$
Kẻ $RN\perp MP$. Dễ thấy $NRQP$ là hình chữ nhật nên $NR=PQ=40$ (cm)
$MN=MP-RQ=15-6=9$ (cm)
Độ dài băng chuyền: $MR=\sqrt{NM^2+NR^2}=\sqrt{9^2+40^2}=41$ (cm)
---------
b. Bạn không cho biết $B,H,A,C$ là những điểm nào?


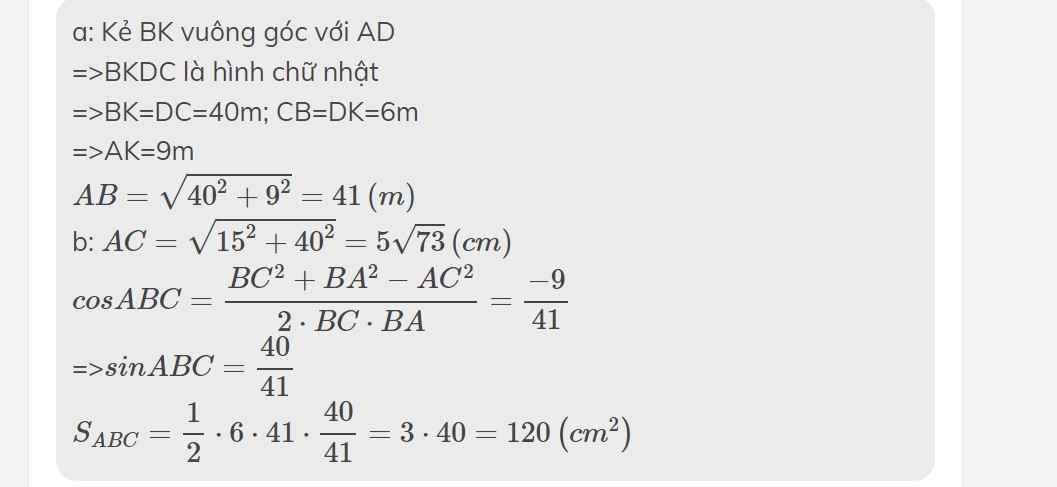
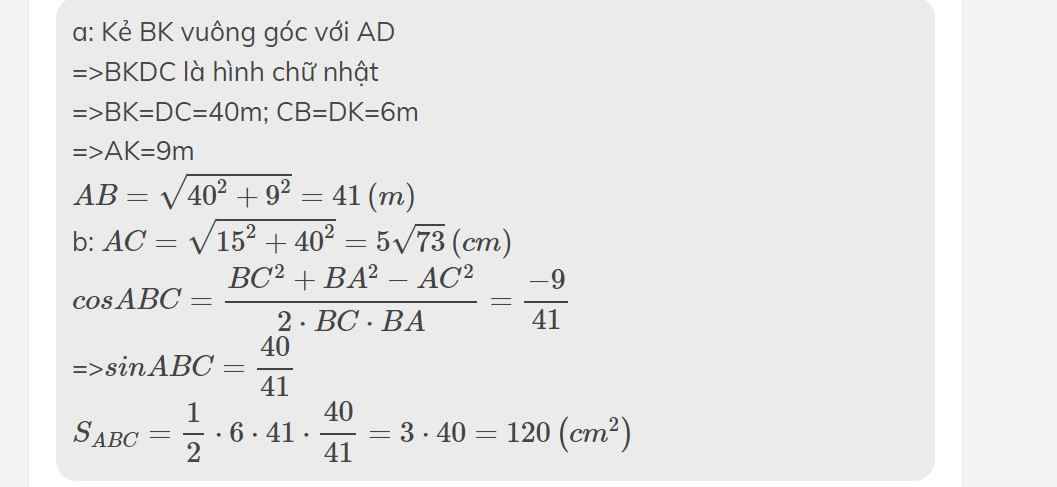
AB=150m