Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB
Xét tứ giác AIBD có
E là trung điểm của AB
E là trung điểm của ID
Do đó: AIBD là hình bình hành
mà AB\(\perp\)DI
nên AIBD là hình thoi

a: Xét tứ giác AEDF có
góc AED=góc AFD=góc FAE=90 độ
nên AEDF là hình chữ nhật
b: Xét ΔABC có CF/CA=CD/CB
nên DF//AB và DF=AB/2
=>Di//AB và DI=AB
=>ABDI là hình bình hành

a: Xét tứ giác AEDF có
AE//DF
DE//AF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
a, Vì DE//AB nên DE⊥AC và DF//AC nên DF⊥AB
Vì \(\widehat{AED}=\widehat{AFD}=\widehat{EAF}=90^0\) nên AEDF là hcn
b,Vì E là trung điểm MD và AC nên AMCD là hbh
Mà AC⊥DE nên AMCD là hthoi
c, Vì D là trung điểm BC và AK và \(\widehat{BAC}=90^0\) nên ABKC là hcn
Để ABKC là hv thì AB=AC hay tam giác ABC vuông cân tại A

Để chứng minh các phần a, b và c, ta sẽ sử dụng các tính chất của tam giác vuông và hình chữ nhật.
a. Ta có tam giác ABC vuông tại A, nên theo định lí trung tuyến, ta có DE là đường trung tuyến của tam giác ABC. Do đó, DE song song với cạnh AC. Tương tự, ta có DF song song với cạnh AB. Vậy DE//AC và DF//AB.
b. Ta cần chứng minh AEDF là hình chữ nhật. Đầu tiên, ta thấy DE//AC và DF//AB (theo phần a). Khi đó, ta có:
- AD = DC (vì D là trung điểm của BC)
- AE = EB (vì E là trung điểm của AB)
- AF = FC (vì F là trung điểm của AC)
Vậy ta có các cạnh đối diện của tứ giác AEDF bằng nhau, do đó AEDF là hình chữ nhật.
c. Gọi M là điểm đối xứng của D qua AB. Ta cần chứng minh M đối xứng với N qua A. Để làm điều này, ta sẽ chứng minh AM = AN và góc MAN = góc NAM.
- Vì M là điểm đối xứng của D qua AB, nên ta có AM = AD.
- Vì N là điểm đối xứng của D qua AC, nên ta có AN = AD.
Do đó, ta có AM = AN.
- Ta có góc MAD = góc DAB (vì M là điểm đối xứng của D qua AB)
- Ta có góc NAD = góc DAC (vì N là điểm đối xứng của D qua AC)
Vì tam giác ABC vuông tại A, nên góc DAB = góc DAC. Từ đó, ta có góc MAD = góc NAD.
Vậy ta có AM = AN và góc MAN = góc NAM, do đó M đối xứng với N qua A.
Vậy ta đã chứng minh được M đối xứng với N qua A.

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
b: Xét tứ giác ADBG có
E là trung điểm của AB
E là trung điểm của DG
Do đó: ADBG là hình bình hành
mà DA=DB
nên ADBG là hình thoi
c: Xét ΔABC có
D là trung điểm của BC
E là trung điểm của AB
Do đó: DE là đường trung bình
=>DE//AC và DE=AC/2
hay DE=CF và DE//CF
=>EDCF là hình bình hành

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

a)
D là trung điểm của BC (gt)
mà DF // AB (AB _I_ AC; DF _I_ AC)
=> F là trung điểm của AC
mà D là trung điểm của BC (gt)
=> DF là đường trung bình của tam giác CAB
=> DF = \(\frac{1}{2}\)AB = 10 : 2 = 5 (cm)
b)
D là trung điểm của BC
mà DE // AC (DE _I_ AB; AC _I_ AB)
=> E là trung điểm của AB
mà E là trung điểm của MD (M đối xứng D qua AB)
=> ADBM là hình bình hành
mà AB _I_ MD (M đối xứng D qua AB)
=> ADBM là hình thoi
c)
DEA = EAF = AFD = 900
=> AEFD là hình chữ nhật
=> AEFD là hình vuông
<=> AD là tia phân giác của BAC
mà AD là đường trung tuyến của tam giác ABC vuông tại A (D là trung điểm của BC)
=> Tam giác ABC vuông cân tại A
Bạn tự vẽ hình nha!!!
Ta có:
\(AC \perp AB\) (\(\Delta ABC\) vuông tại A (gt))
\(AC \perp DF\) (gt)
\(\Rightarrow\) AB // DF (Định lí 1 bài từ vuông góc đến song song)
mà D là trung điểm BC (gt)
\(\Rightarrow\) F là trung điểm của AC (Định lí 1 bài đường trung bình của tam giác)
Xét \(\Delta ABC\) có:
D là trung điểm BC (gt)
F là trung điểm của AC (cmt)
\(\Rightarrow\) DF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DF=\frac{AB}{2}=\frac{10}{2}=5\left(cm\right)\)
b) Chứng minh tương tự ta có E là trung điểm AB
Xét tứ giác ADBM có:
\(\Rightarrow EM=ED\) (M đối xứng với D qua AB (gt))
\(EA=EB\left(cmt\right)\)
MD giao AB tại E (gt)
\(\Rightarrow\) Tứ giác ADBM là hình bình hành (dhnb)
mà \(AB \perp MD\) (M đối xứng với D qua AB (gt))
\(\Rightarrow\) Tứ giác ADBM là hình thoi (dhnb)
c) Xét tứ giác AEDF có:
\(\widehat{EAF} = 90^0\) (\(\Delta ABC\) vuông tại A (gt))
\(\widehat{AED} = 90^0\) (\(MD \perp AB\))
\(\widehat{AFD} = 90^0\) (\(DF \perp AC\))
\(\Rightarrow\) Tứ giác AEDF là hình chữ nhật (dhnb)
Để hình chứ nhật AEDF
\(\Leftrightarrow\) AEDF là hình thoi
\(\Leftrightarrow\) AD là tia phân giác của \(\Delta ABC\) (vì AD là đường trung tuyến)
\(\Leftrightarrow\) \(\Delta ABC\) cân tại A (vì \(\Delta ABC\) vuông tại A (gt))
\(\Leftrightarrow\)\(\Delta ABC\) vuông cân tại A
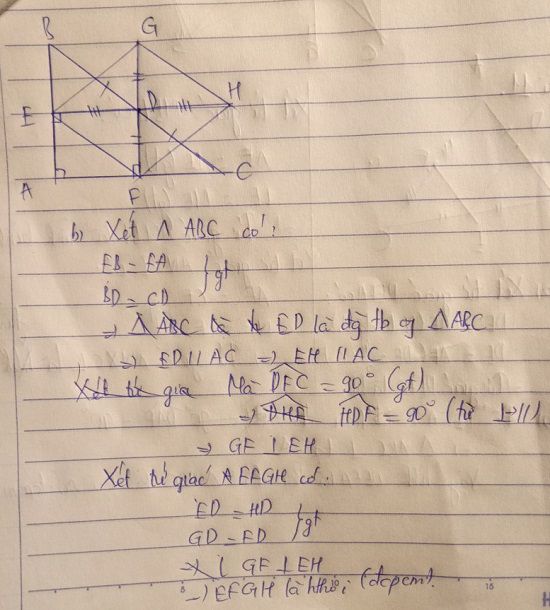

Bài 2:
b: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
giúp em với mn ơi