
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(-x-2=\dfrac{5}{4}\)
\(\Leftrightarrow x=-2-\dfrac{5}{4}\)
\(\Leftrightarrow x=-\dfrac{13}{4}\)


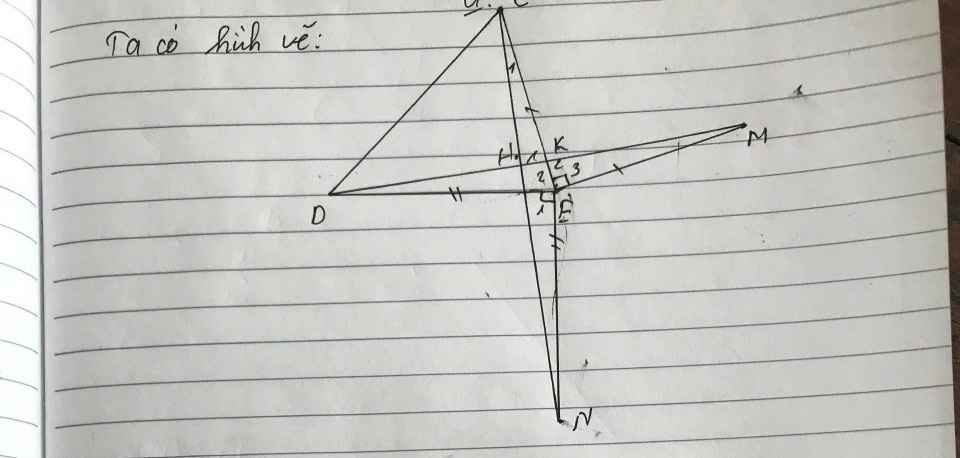
a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN

Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)

Bài 1: - \(\dfrac{5}{7}\) x \(\dfrac{31}{33}\) + \(\dfrac{-5}{7}\) x \(\dfrac{2}{33}\) + 2\(\dfrac{5}{7}\)
= - \(\dfrac{5}{7}\) \(\times\) ( \(\dfrac{31}{33}\) + \(\dfrac{2}{33}\)) + 2 + \(\dfrac{5}{7}\)
= - \(\dfrac{5}{7}\) + 2 + \(\dfrac{5}{7}\)
= 2
2, \(\dfrac{3}{14}\): \(\dfrac{1}{28}\) - \(\dfrac{13}{21}\): \(\dfrac{1}{28}\) + \(\dfrac{29}{42}\): \(\dfrac{1}{28}\) - 8
= (\(\dfrac{3}{14}\) - \(\dfrac{13}{21}\) + \(\dfrac{29}{42}\)) : \(\dfrac{1}{28}\) - 8
= \(\dfrac{2}{7}\) x 28 - 8
= 8 - 8
= 0









Vì tam giác ABH vuông tại H
\(\Rightarrow AH^2+x^2=AB^2\)
mà AH = 4,8 cm; AB = 6 cm
\(\Rightarrow4,8^2+x^2=6^2\) \(\Rightarrow23,04+x^2=36\) \(\Rightarrow x^2=36-23,04=12,96\) \(\Rightarrow x=3,6\left(cm\right)\)
Vì tam giác ACH vuông tại H
\(\Rightarrow AH^2+y^2=AC^2\)
mà AH = 4,8 cm; AC = 8 cm
\(\Rightarrow4,8^2+y^2=8^2\) \(\Rightarrow23,04+y^2=64\) \(\Rightarrow y^2=64-23,04=40,96\) \(\Rightarrow y=6,4\left(cm\right)\)
Vậy x = 3,6 cm; y = 6,4 cm
~~ Chúc bạn học tốt ~~
áp dụng định lí Py-ta-go vào \(\Delta\) vuông AHC, ta có:
\(AC^2=AH^2+HC^2\)
\(\Rightarrow\)\(HC^2=AC^2-AH^2\)
\(HC^2=8^2-4,8^2\)
\(HC^2=64-23,04\)
\(HC^2=40,96\)
\(\Rightarrow\)\(HC=\sqrt{40,96}=6,4\)
vậy \(y\)\(=\)\(6,4\)