
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.a) = x^12 : x^6 = x^6
b) = (-x)^2=x^2
c) = 1/2.xy^3
d) -3/2.x^2.y
e) = (-xy)^7
f) = -4x^2 + 4xy - 6y^2
g) = xy - 2x + 4y
Bài 1:
a: A chia hết cho B
b: A chia hết cho B
c: A không chia hết cho B
d: A không chia hết cho B

Bài 1:
b) \(B=A.\dfrac{-10}{x-4}=\dfrac{x-4}{x+5}.\dfrac{-10}{x-4}=\dfrac{-10}{x+5}\)
Để B nguyên <=> x+5 nguyên mà \(x\in Z\Rightarrow x+5\inƯ\left(-10\right)=\left\{\pm1;\pm2;\pm5;\pm10\right\}\)
\(\Leftrightarrow x\in\left\{-6;-4;-3;-7;0;-10;-15;5\right\}\) kết hợp với điều kiện của x
\(\Rightarrow x\in\left\{-15;-10;-6;-7;-3;0;5\right\}\)
Bài 5:
Có \(\left|x-2018\right|+\left|2x-2019\right|+\left|3x-2020\right|\ge0\) \(\forall\)x
\(\Rightarrow x-2021\ge0\) \(\Leftrightarrow x\ge2021\)
\(\Rightarrow x-2018>0,2x-2019>0,3x-2020>0\)
PT \(\Leftrightarrow x-2018+2x-2019+3x-2020=x-2021\)
\(\Leftrightarrow5x=4036\) \(\Leftrightarrow x=\dfrac{4036}{5}< 2021\) (L)
Vậy pt vô nghiệm

Bài 1:
a: Xét tứ giác BEDF có
ED//BF
ED=BF
Do đó: BEDF là hình bình hành
Suy ra: BE=DF
c: ta có: BEDF là hình bình hành
nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường
mà AC và BD cắt nhau tại trung điểm của mỗi đường
nên AC,BD,EF đồng quy

Câu 2:
a: Ta có: \(25x^2-9=0\)
\(\Leftrightarrow\left(5x-3\right)\left(5x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{5}\\x=-\dfrac{3}{5}\end{matrix}\right.\)
b: Ta có: \(\left(x-4\right)^2-\left(x-2\right)\left(x+2\right)=6\)
\(\Leftrightarrow x^2-8x+16-x^2+4=6\)
\(\Leftrightarrow-8x=-14\)
hay \(x=\dfrac{7}{4}\)
c: Ta có: \(\left(2x-1\right)^2+\left(x+3\right)^2-5\left(x-7\right)\left(x+7\right)=0\)
\(\Leftrightarrow4x^2-4x+1+x^2+6x+9-5\left(x^2-49\right)=0\)
\(\Leftrightarrow5x^2+2x+10-5x^2+245=0\)
\(\Leftrightarrow x=-\dfrac{255}{2}\)

1:
a: \(=4x^2+4x+1-x^2-4x+5\)
\(=3x^2+6\)
b: \(=9x^2-24x+16+\left(2x-3\right)^2\)
\(=9x^2-24x+16+4x^2-12x+9\)
\(=13x^2-36x+25\)
c: \(=2\left(x^2-2x+1\right)-3\left(x^2+6x+9\right)+4x^2-1\)
\(=2x^2-4x+2-3x^2-18x-27+4x^2-1\)
\(=3x^2-22x-26\)

10: (4x+20)(2x-6)=0
=>(x+5)(x-3)=0
=>x=-5 hoặc x=3
11: =>(2x-1)(2x+1)=0
=>x=1/2 hoặc x=-1/2
12:=>(x-1)(x-3)=0
=>x=1 hoặc x=3
7: \(\Leftrightarrow x^2-4x+4-x^2-2x=2x-12\)
=>-6x+4=2x-12
=>-8x=-16
hay x=2(loại)


Gọi h là độ dài chiều cao của đỉnh A ứng với cạnh BC
Ta có, diện tích tam giác ABC là: \(S_{ABC}=\dfrac{1}{2}h.BC=90\left(cm^2\right)\left(1\right)\)
Lại có, diện tích tam giác ABM là: \(S_{ABM}=\dfrac{1}{2}h.BM\left(2\right)\)
Lấy (1) chia (2) ta có: \(\dfrac{BC}{BM}=\dfrac{90}{S_{ABM}}\Leftrightarrow\dfrac{4BM}{BM}=\dfrac{90}{S_{ABM}}\Leftrightarrow4=\dfrac{90}{S_{ABM}}\Rightarrow S_{ABM}=22,5cm^2\)

Xét ΔACB có
BF,CE là trung tuyến
BF cắt CE tạiI
=>I là trọng tâm
=>EI/IC=1/2
 giúp bài 1 với
giúp bài 1 với


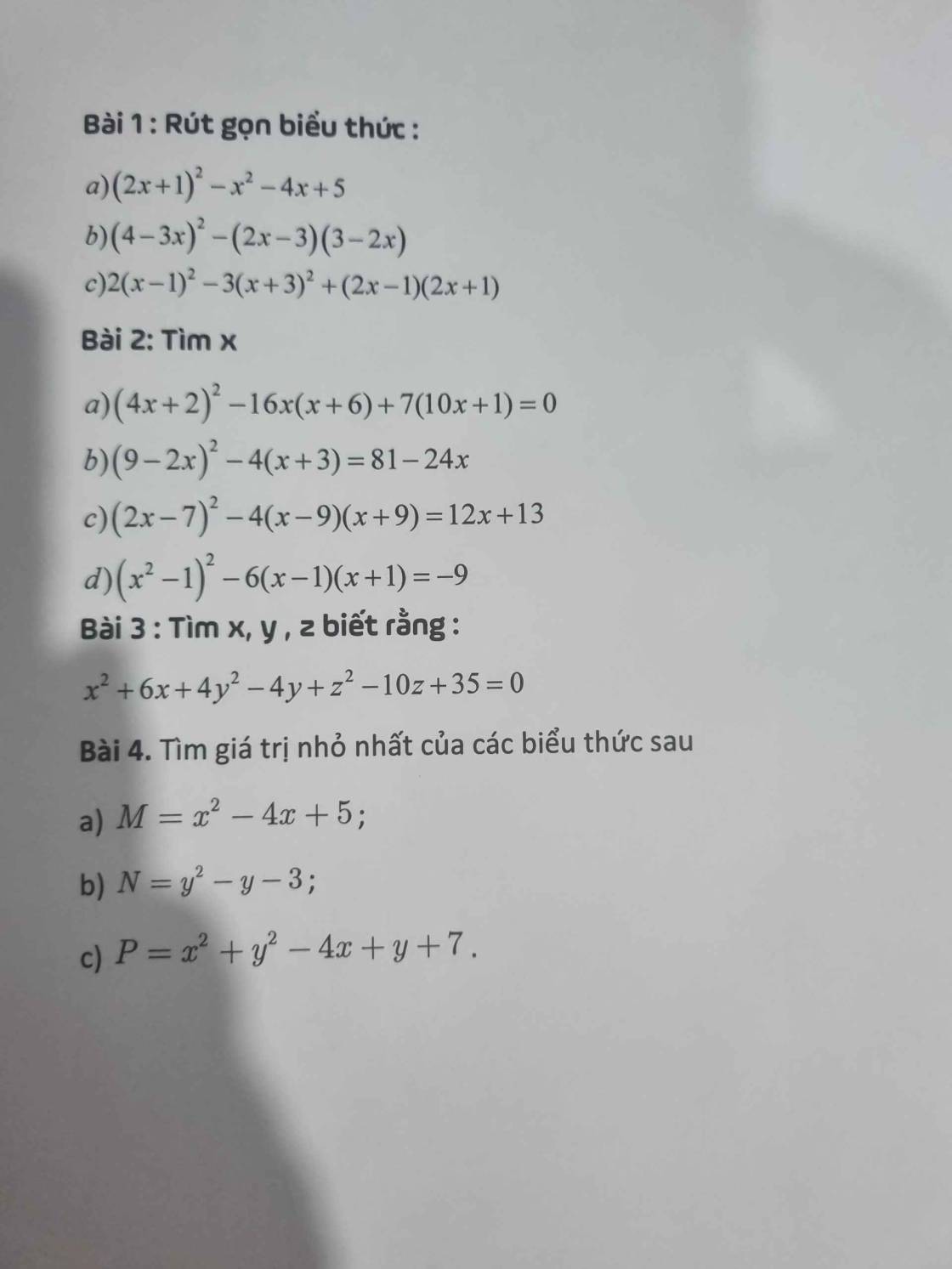



giúp với
no