
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
b: Ta có: \(B=\dfrac{15-5\sqrt{x}}{x-5\sqrt{x}+6}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{-5\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-2}=1\)


3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8

a) Ta có: \(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2\)
\(=\left(a+2\sqrt{a}+1\right)\cdot\left(\dfrac{1}{\sqrt{a}+1}\right)^2\)
\(=1\)
b) Ta có: \(\dfrac{a+b}{b^2}\cdot\sqrt{\dfrac{a^2b^4}{a^2+2ab+b^2}}\)
\(=\dfrac{a+b}{b^2}\cdot\dfrac{\left|a\right|\cdot b^2}{a+b}\)
=|a|

Điều kiện:`a>=0,a ne 1` $\\$ `E=(1+(a-sqrta)/(sqrta-1))(1-(a+sqrta)/(1+sqrta))`
`=(1+(sqrta(sqrta-1))/(sqrta-1))(1-(sqrta(sqrta+1))/(sqrta+1))`
`=(1+sqrta)(1-sqrta)`
`=1-a`
\(E=\left(1+\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
ĐK: a ≥ 0; a khác 1
\(=\left[1+\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right]\left[1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\right]\)
\(=\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)=1-a\)

Δ=(2m-6)^2-4(m^2+3)
=4m^2-24m+36-4m^2-12=-24m+24
Để phương trình có hai nghiệm phân biệt thì -24m+24>0
=>m<1
x1^2+x2^2=36
=>(x1+x2)^2-2x1x2=36
=>(2m-6)^2-2(m^2+3)=36
=>4m^2-24m+36-2m^2-6-36=0
=>2m^2-24m-6=0
=>m^2-12m-3=0
=>\(m=6-\sqrt{39}\)

b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)

1.
$(m^2-m-1)x-5m=(3-m)x$
$\Leftrightarrow (m^2-m-1+m-3)x=5m$
$\Leftrightarrow (m^2-4)x=5m$
$\Leftrightarrow (m-2)(m+2)x=5m$
Nếu $m=-2$ thì $0x=-10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m=2$ thì $0x=10$ (vô lý) $\Rightarrow$ pt vô nghiệm
Nếu $m\neq \pm 2$ thì pt có nghiệm duy nhất $x=\frac{5m}{(m-2)(m+2)}$
2.
$m^2x+mx+x-m-2=0$
$\Leftrightarrow x(m^2+m+1)=m+2$
Vì $m^2+m+1=(m+\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $m\in\mathbb{R}$
$\Rightarrow m^2+m+1\neq 0$
Do đó pt có nghiệm duy nhất $x=\frac{m+2}{m^2+m+1}$ với mọi $m\in\mathbb{R}$

đề như thế này à \(\dfrac{\sqrt{27-3\sqrt{2}+2\sqrt{6}}}{3\sqrt{3}}\)




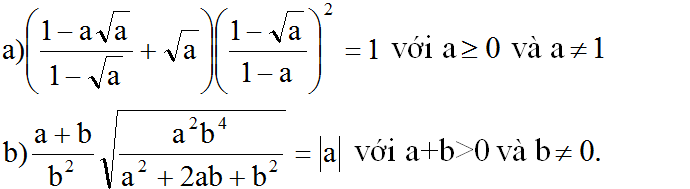
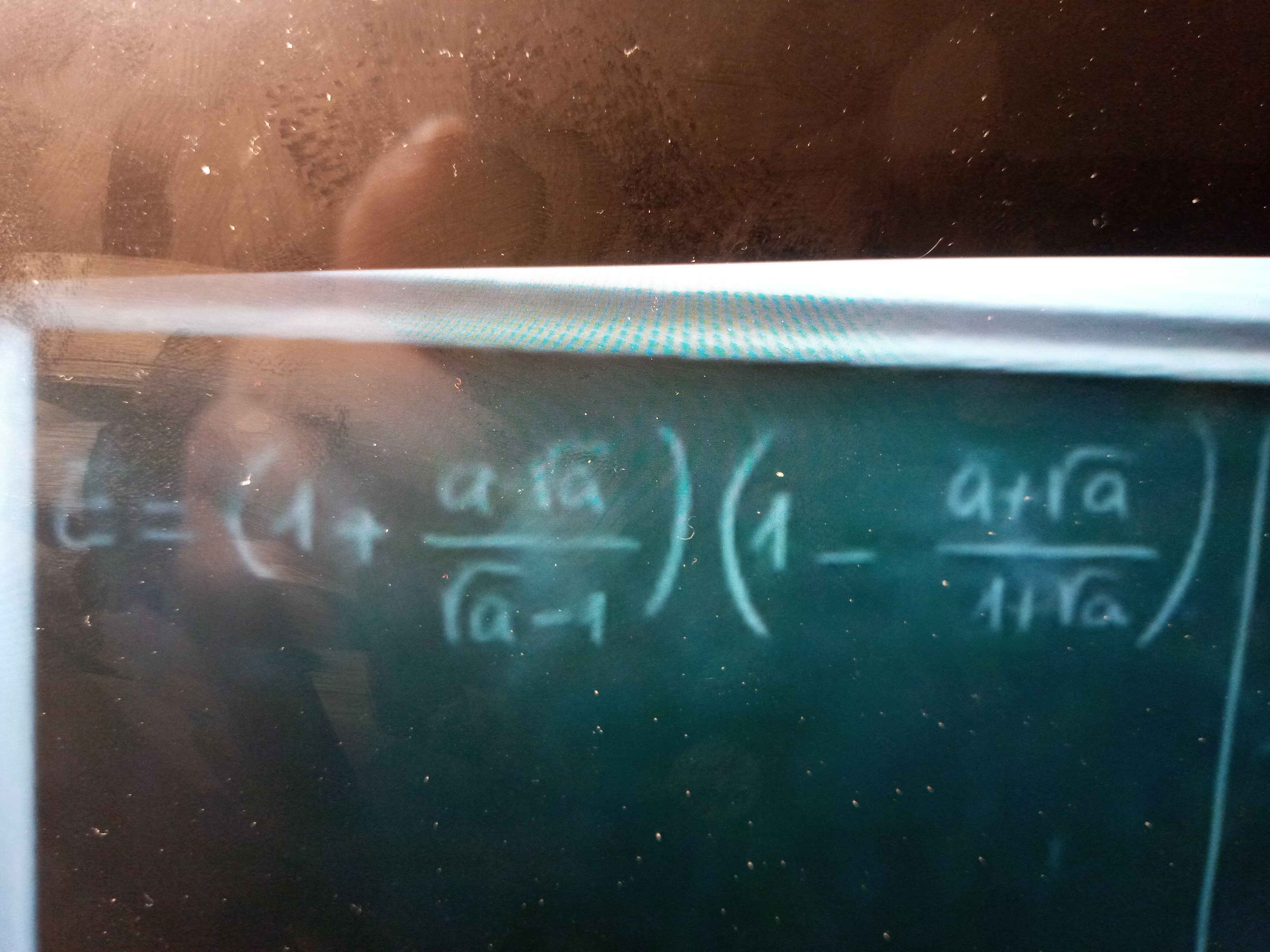
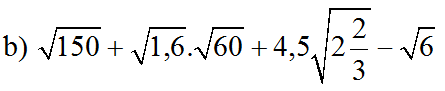

1: góc DMB+góc DHB=180 độ
=>DMBH nội tiếp
2: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC
góc AMD+góc AND=180 độ
=>AMDN nội tiếp
=>góc ANM=góc ADM=góc ABH
=>góc ANM=góc xAC
=>Ax//MN