a.

\(y'=\left(x^2\right)'+\left(4sinx\right)'=2x+4cosx\)

b.

\(y'=\left(2x^3\right)'-\left(sinx\right)'+\left(2\right)'=6x^2-cosx\)

c.

\(y'=\left(5sin\left(x-\dfrac{\pi}{4}\right)\right)'=5.\left(x-\dfrac{\pi}{4}\right)'.cos\left(x-\dfrac{\pi}{4}\right)=5cos\left(x-\dfrac{\pi}{4}\right)\)

4a.

\(y=2x^2-tanx\Rightarrow y'=\left(2x^2\right)'-\left(tanx\right)'=4x-\dfrac{1}{cos^2x}\)

b.

\(y'=\left(3tan\left(x+\dfrac{\pi}{3}\right)\right)'-\left(4sinx\right)'=3\left(x+\dfrac{\pi}{3}\right)'.\dfrac{1}{cos^2\left(x+\dfrac{\pi}{3}\right)}-4cosx\)

\(=\dfrac{3}{cos^2\left(x+\dfrac{\pi}{3}\right)}-4cosx\)

5a.

\(y'=\left(2x\right)'-\left(3sinx\right)'+\left(2cotx\right)'=2-3cosx-\dfrac{2}{sin^2x}\)

b.

\(y'=\left(cot\left(3x+\dfrac{\pi}{6}\right)\right)'-\left(4cosx\right)'=\left(3x+\dfrac{\pi}{6}\right)'.\dfrac{-1}{sin^2\left(3x+\dfrac{\pi}{6}\right)}+4sinx\)

\(=-\dfrac{3}{sin^2\left(3x+\dfrac{\pi}{6}\right)}+4sinx\)

1.

\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng

\(f\left(-x\right)=\left(-x^3-x\right)tan\left(-3x\right)=\left(x^3+x\right)tan3x=f\left(x\right)\)

Hàm chẵn

2.

\(D=R\)

\(f\left(-x\right)=\left(-2x+1\right)sin\left(-5x\right)=\left(2x-1\right)sin5x\ne\pm f\left(x\right)\)

Hàm không chẵn không lẻ 

3.

\(D=R\backslash\left\{\dfrac{\pi}{6}+\dfrac{k\pi}{3}\right\}\) là miền đối xứng

\(f\left(-x\right)=tan\left(-3x\right).sin\left(-5x\right)=-tan3x.\left(-sin5x\right)=tan3x.sin5x=f\left(x\right)\)

Hàm chẵn

4.

\(D=R\)

\(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-10x\right)=sin^22x+cos10x=f\left(x\right)\)

Hàm chẵn

5.

\(D=R\backslash\left\{k\pi\right\}\) là miền đối xứng

\(f\left(-x\right)=\dfrac{-x}{sin\left(-x\right)}=\dfrac{-x}{-sinx}=\dfrac{x}{sinx}=f\left(x\right)\)

Hàm chẵn

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)

\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)

\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)

\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)

\(\Rightarrow\) vô nghiệm.

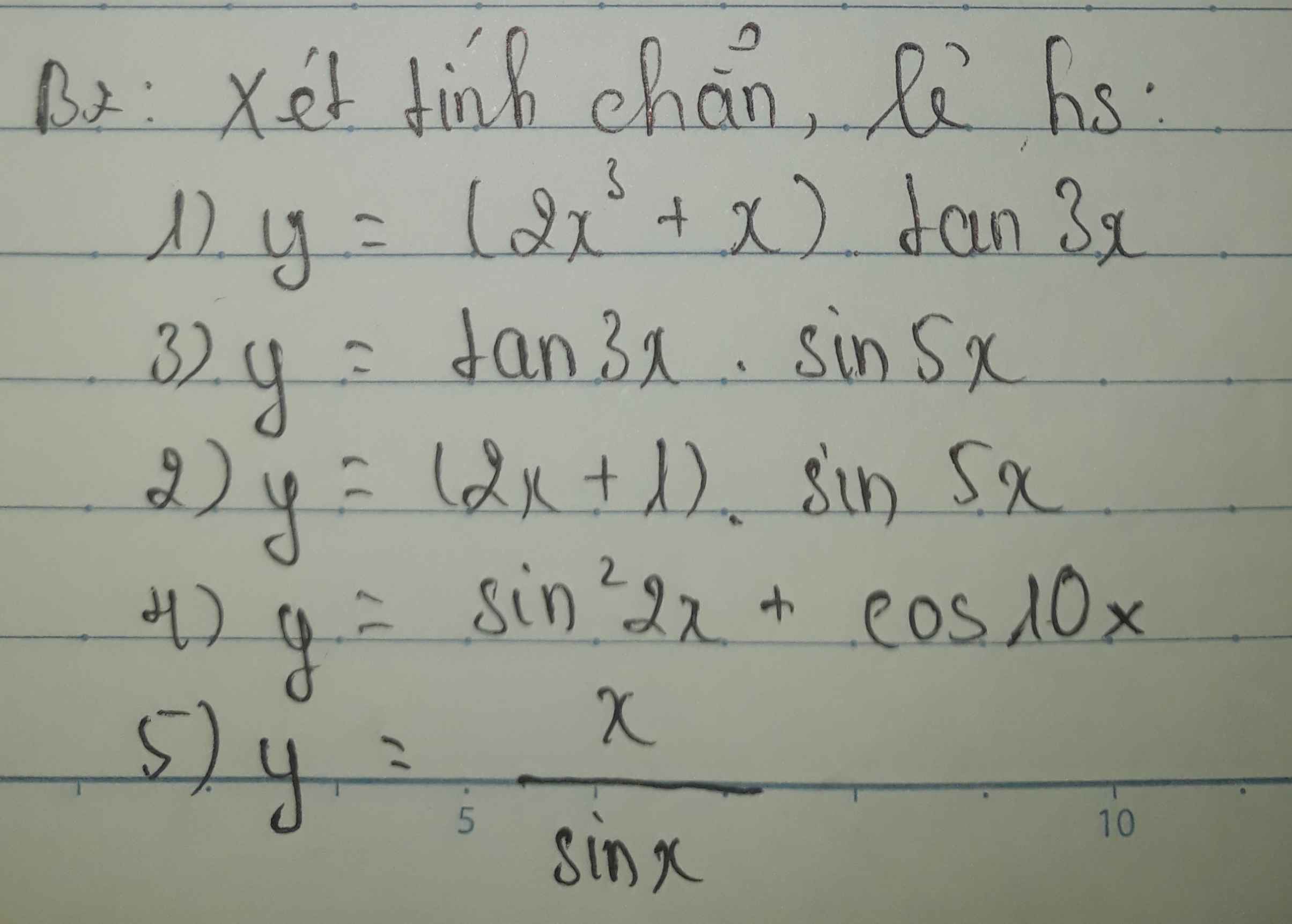
thì ko hoặc có