
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


13.
Có \(3!\) cách sắp xếp 3 người phái đoàn Anh ngồi cạnh nhau.
Có \(5!\) cách sắp xếp 5 người phái đoàn Pháp ngồi cạnh nhau.
Có \(7!\) cách sắp xếp 7 người phái đoàn Mỹ ngồi cạnh nhau.
Có \(2!\) cách sắp xếp 3 phái đoàn vào bàn tròn.
\(\Rightarrow\) Có \(\Rightarrow3!.5!.7!.2!=7257600\) cách sắp xếp thỏa mãn yêu cầu bào toán.

14.
A là khẳng định sai, CD không vuông góc SB
(Vì nếu \(CD\perp SB\) (1); do \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SAB\right)\Rightarrow CD\perp AB\) (vô lý do \(CD||AB\))


14.
Hàm số ko xác định tại \(x=-1,x=2\) nên gián đoạn tại \(x=-1,x=2\)
A đúng
15.
\(\lim\limits_{x\rightarrow1^-}\dfrac{2x+1}{x-1}=-\infty\)
(Do \(\lim\limits_{x\rightarrow1^-}\left(2x+1\right)=3>0\) và \(x-1< 0\) khi \(x< 1\))

\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)
\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\)
Suy ra : a/b = 2/3 => a - b = -1

c.
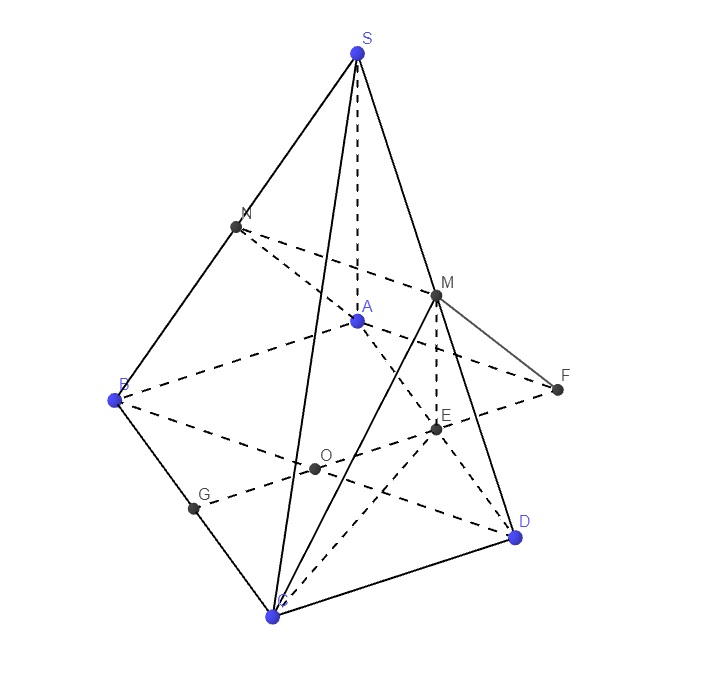
Gọi E là trung điểm AD \(\Rightarrow EM\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}EM=\dfrac{1}{2}SA=a\\EM||SA\Rightarrow EM\perp\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow EC\) là hình chiếu vuông góc của CM lên (ABCD)
\(\Rightarrow\widehat{MCE}\) là góc giữa SM và (ABCD)
\(ED=\dfrac{1}{2}AD=a\Rightarrow EC=\sqrt{CD^2+ED^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{MCE}=\dfrac{EM}{EC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{MCE}=...\)
e.
Gọi O là trung điểm BD, qua A kẻ đường thẳng song song BD cắt OE kéo dài tại F
\(\Rightarrow ABOF\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow\left\{{}\begin{matrix}AF=OB=\dfrac{1}{2}BD\\AF||BD\end{matrix}\right.\)
Lại có MN là đường trung bình tam giác SBD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}MN=AF\\MN||AF\end{matrix}\right.\) \(\Rightarrow ANMF\) là hình bình hành
\(\Rightarrow AN||MF\Rightarrow\left(AN;CM\right)=\left(AN;MF\right)=\widehat{CMF}\) nếu nó ko tù hoặc bằng góc bù của nó nếu \(\widehat{CMF}\) là góc tù
Ta có: \(MF=AN=\dfrac{a\sqrt{5}}{2}\) ; \(CM=\sqrt{CE^2+EM^2}=a\sqrt{3}\)
ABOF là hình bình hành nên AODF cũng là hình bình hành \(\Rightarrow E\) là tâm hình bình hành
\(\Rightarrow EF=OF=\dfrac{AB}{2}=\dfrac{a}{2}\)
Gọi G là giao điểm OE và BC \(\Rightarrow FG=EG+EF=a+\dfrac{a}{2}=\dfrac{3a}{2}\)
\(\Rightarrow CF=\sqrt{FG^2+CG^2}=\dfrac{a\sqrt{13}}{2}\)
ĐỊnh lý hàm cos:
\(cos\widehat{CMF}=\dfrac{CM^2+MF^2-CF^2}{2CM.MF}=\dfrac{\sqrt{15}}{15}\Rightarrow\widehat{CMF}\)

Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8
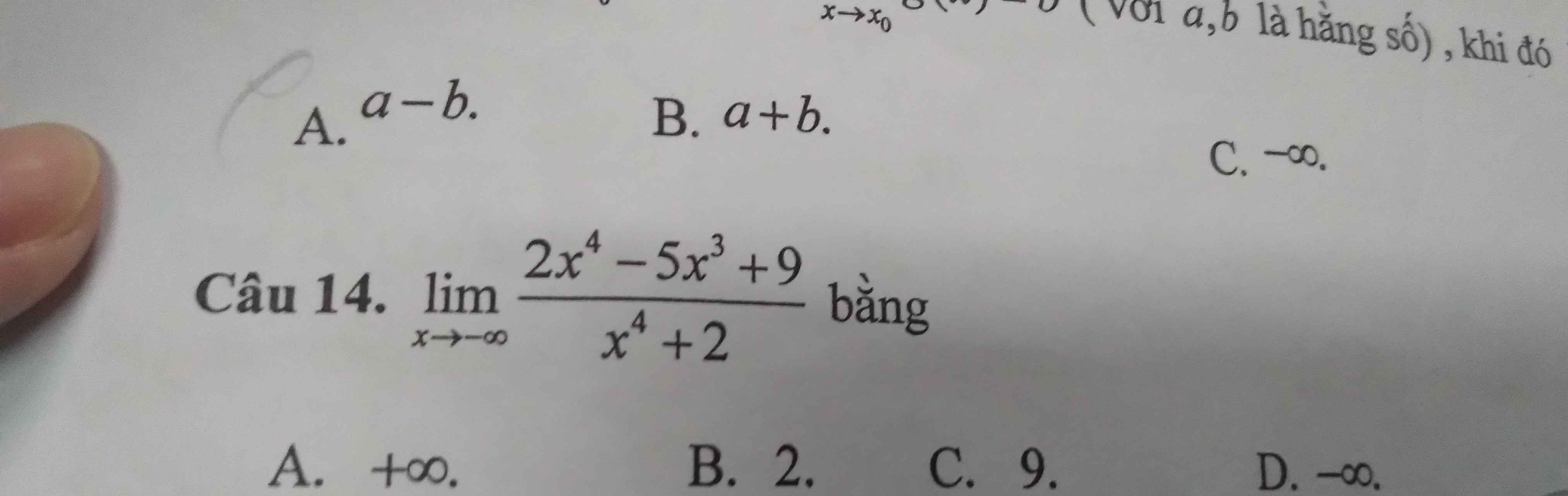









\(\lim\limits_{x\rightarrow+\infty}\dfrac{2x^4-5x^3+9}{x^4+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{2-\dfrac{5}{x}+\dfrac{9}{x^4}}{1+\dfrac{2}{x^4}}=\dfrac{2-0+0}{1+0}=2\)