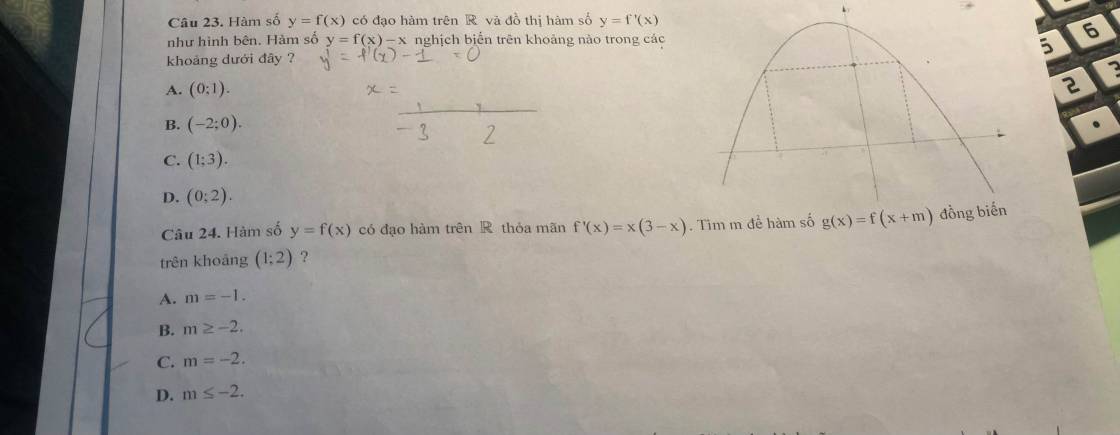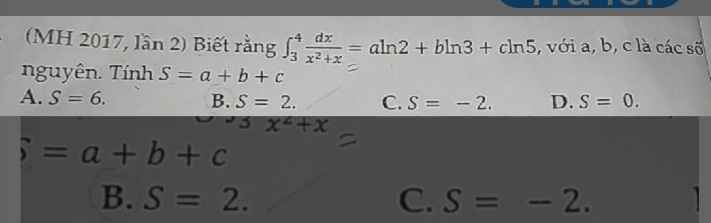Mấy câu này thuộc bài đồng biến nghịch biến nha!!!! 

Câu này ý D á bạn

bạn tính đạo hàm của f'(3-x²) ra á xong cho bằng k rồi cho các nghiệm đan dấu rồi xét 

12. \(\dfrac{4\sqrt{3}}{3}\pi\)

13. \(12\pi\)

14. \(\sqrt{6}\pi a^2\)

\(\int\limits^4_3\dfrac{dx}{x^2+x}=\int\limits^4_3\dfrac{dx}{x\left(x+1\right)}=\int\limits^4_3\left(\dfrac{1}{x}-\dfrac{1}{x+1}\right)dx=\left[lnx-ln\left(x+1\right)\right]|^4_3\)

\(=ln4-ln5-\left(ln3-ln4\right)=2ln4-ln3-ln5\)

\(=4ln2-ln3-ln5\Rightarrow a=4;b=c=-1\)

\(\Rightarrow S=2\)

a

Chọn A

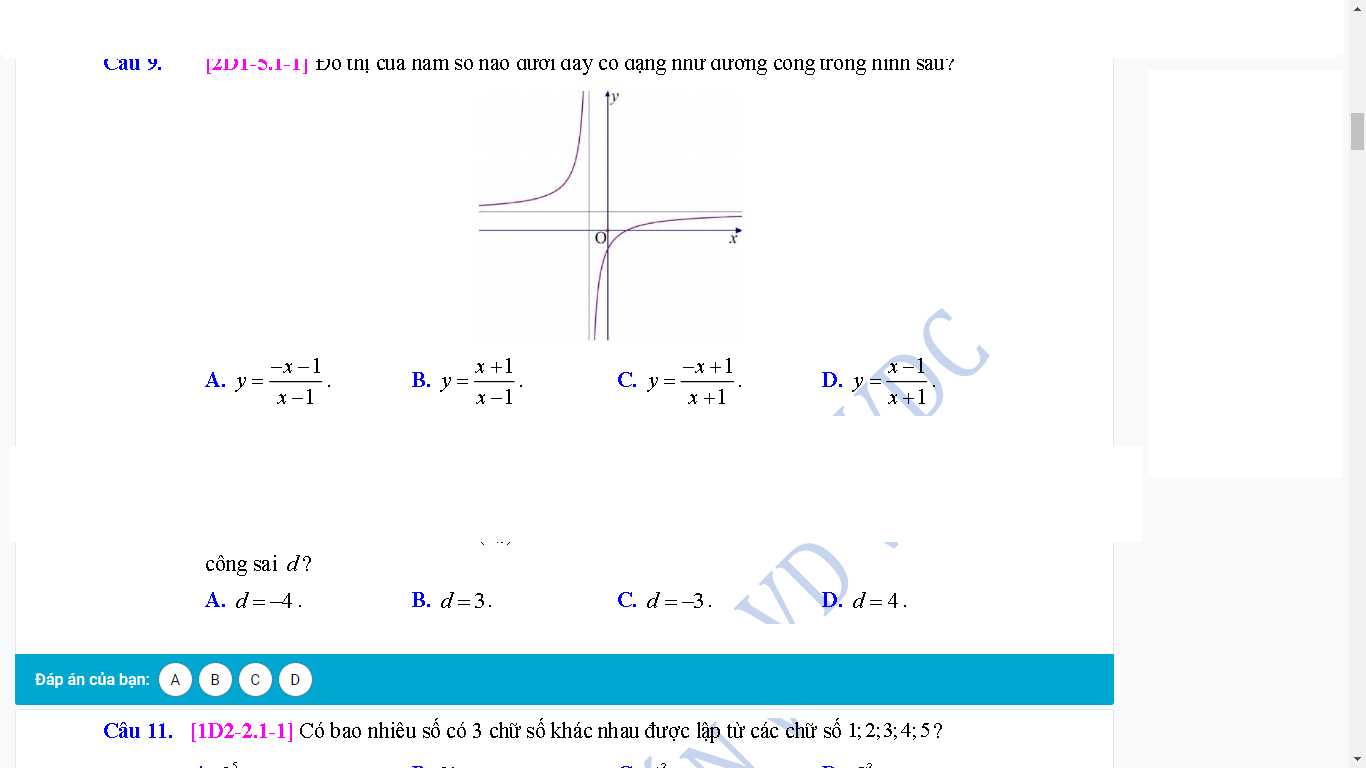
- Tiệm cận đứng của đồ thị là 1 giá trị âm nên loại A và B

- Hàm đồng biến trên các khoảng xác định nên loại C

Vậy D là đáp án đúng

Xét \(I_1=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}\dfrac{f\left(tanx\right)}{cos^2x}dx=\int\limits^{\dfrac{\pi}{3}}_{\dfrac{\pi}{4}}f\left(tanx\right)d\left(tanx\right)\)

Đặt \(tanx=t\Rightarrow t\in\left[1;\sqrt{3}\right]\Rightarrow f\left(t\right)=2t^3-t\)

\(I_1=\int\limits^{\sqrt{3}}_1f\left(t\right)dt=\int\limits^{\sqrt{3}}_1\left(2t^3-t\right)dt=3\)

Xét \(I_2=\int\limits^{\sqrt{e-1}}_0\dfrac{xf\left(ln\left(x^2+1\right)\right)}{x^2+1}dx=\dfrac{1}{2}\int\limits^{\sqrt{e-1}}_0f\left(ln\left(x^2+1\right)\right).d\left[ln\left(x^2+1\right)\right]\)

Đặt \(ln\left(x^2+1\right)=t\Rightarrow t\in\left[0;1\right]\Rightarrow f\left(t\right)=-3t+4\)

\(I_2=\dfrac{1}{2}\int\limits^1_0\left(-3t+4\right)dt=\dfrac{5}{4}\)

\(\Rightarrow I=3+\dfrac{5}{4}=\dfrac{17}{4}\Rightarrow P=21\)

16.

Số cạnh của 1 lăng trụ luôn chia hết cho 3 nên A

17.

Chóp có đáy là đa giác n cạnh sẽ có n mặt bên (mỗi cạnh đáy và đỉnh sẽ tạo ra 1 mặt bên tương ứng)

Do đó chóp có n+1 mặt (n mặt bên và 1 mặt đáy)

Chóp có n+1 đỉnh (đáy n cạnh nên có n đỉnh, cộng 1 đỉnh của chóp là n+1)

Do đó số mặt bằng số đỉnh

18. D

19. A

20. C