Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E

5.
\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m-2\right)^2>0\Rightarrow m\ne2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=x_1+x_2\)
\(\Leftrightarrow m^2-2\left(m-1\right)=m\)
\(\Leftrightarrow m^2-3m+2=0\Rightarrow\left[{}\begin{matrix}m=1\\m=2\left(loại\right)\end{matrix}\right.\)
1.
\(\Delta=9+4m>0\Rightarrow m>-\dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1x_2=-m\end{matrix}\right.\)
\(5x_1+5x_2=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5\left(x_1+x_2\right)=1-\left(x_1x_2\right)^2\)
\(\Leftrightarrow5.\left(-3\right)=1-\left(-m\right)^2\)
\(\Leftrightarrow m^2=16\Rightarrow\left[{}\begin{matrix}m=4\\m=-4< -\dfrac{9}{4}\left(loại\right)\end{matrix}\right.\)
2.
\(\Delta=\left(2m+1\right)^2-4\left(m^2+1\right)=4m-3>0\Rightarrow m>\dfrac{3}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+1\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=13\)
\(\Leftrightarrow x_1^2+2x_1+1+x_2^2+2x_2+1=13\)
\(\Leftrightarrow x_1^2+x_2^2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=11\)
\(\Leftrightarrow\left(2m+1\right)^2-2\left(m^2+1\right)+2\left(2m+1\right)=11\)
\(\Leftrightarrow2m^2+8m-10=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-5< \dfrac{3}{4}\left(loại\right)\end{matrix}\right.\)

Bài 5:
\(x^2+2mx+2m-6=0\)
\(\text{Δ}=\left(2m\right)^2-4\left(2m-6\right)\)
\(=4m^2-8m+24\)
\(=4m^2-8m+4+20\)
\(=\left(2m-2\right)^2+20>=20>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-2m}{1}=-2m\\x_1x_2=\dfrac{c}{a}=\dfrac{2m-6}{1}=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2-2x_1x_2=20\)
=>\(\left(-2m\right)^2-4\left(2m-6\right)=20\)
=>\(4m^2-8m+24-20=0\)
=>\(4m^2-8m+4=0\)
=>\(\left(2m-2\right)^2=0\)
=>2m-2=0
=>2m=2
=>m=1(nhận)
Câu 4:
a: \(2x^2-2x-m=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot2\cdot\left(-m\right)\)
\(=4+8m\)
Để phương trình có hai nghiệm phân biệt thì 8m+4>0
=>8m>-4
=>\(m>-\dfrac{1}{2}\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{2}=\dfrac{2}{2}=1\\x_1x_2=\dfrac{c}{a}=\dfrac{-m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\cdot\left(x_1^2+x_2^2\right)=16\)
=>\(\left(1+\dfrac{m}{2}\right)^2+4\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=16\)
=>\(\left(\dfrac{m+2}{2}\right)^2+4\left[1^2-2\cdot\dfrac{-m}{2}\right]=16\)
=>\(\dfrac{1}{4}\left(m^2+4m+4\right)+4\left(1+m\right)=16\)
=>\(\dfrac{1}{4}m^2+m+1+4+4m-16=0\)
=>\(\dfrac{1}{4}m^2+5m-11=0\)
=>\(m^2+20m-44=0\)
=>(m+22)(m-2)=0
=>\(\left[{}\begin{matrix}m+22=0\\m-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=-22\left(loại\right)\\m=2\left(nhận\right)\end{matrix}\right.\)
5.
\(\Delta'=1+2m\)
a.
Phương trình có 2 nghiệm pb khi:
\(1+2m>0\Rightarrow m>-\dfrac{1}{2}\)
b.
Khi pt có 2 nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=-\dfrac{m}{2}\end{matrix}\right.\)
\(\left(1-x_1x_2\right)^2+4\left(x_1^2+x_2^2\right)=16\)
\(\Leftrightarrow\left(1-x_1x_2\right)^2+4\left(x_1+x_2\right)^2-8x_1x_2=16\)
\(\Leftrightarrow\left(1+\dfrac{m}{2}\right)^2+4.1^2+4m=16\)
\(\Leftrightarrow\dfrac{m^2}{4}+5m-11=0\Rightarrow\left[{}\begin{matrix}m=2\\m=-22< -\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
5.
\(\Delta'=m^2-\left(2m-6\right)=\left(m-1\right)^2+5>0;\forall m\)
Pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=4x_1x_2+20\)
\(\Leftrightarrow4m^2=4\left(2m-6\right)+20\)
\(\Leftrightarrow m^2-2m+1=0\Rightarrow m=1\)

a: ΔABC vuông tại B
=>\(\widehat{A}+\widehat{C}=90^0\)
=>\(\widehat{A}=50^0\)
Xét ΔBAC vuông tại B có
\(sinC=\dfrac{AB}{AC}\)
=>\(AC=\dfrac{6}{sin40}\simeq9,33\left(cm\right)\)
ΔBAC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC=\sqrt{9.33^2-6^2}\simeq7,14\left(cm\right)\)
b: ΔBAC vuông tại B có BH là đường cao
nên \(HC\cdot HA=BH^2\left(1\right)\)
ΔBHC vuông tại H có HI là đường cao
nên \(BI\cdot BC=BH^2\left(2\right)\)
Từ (1),(2) suy ra \(HC\cdot HA=BI\cdot BC\)
c: ΔBHA vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\left(3\right)\)
Từ (2),(3) suy ra \(BI\cdot BC=BM\cdot BA\)
=>\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Xét ΔBIM vuông tại B và ΔBAC vuông tại B có
\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Do đó: ΔBIM đồng dạng với ΔBAC

a: A(1;-3); B(2;4); C(-1;2)
\(AB=\sqrt{\left(2-1\right)^2+\left(4+3\right)^2}=5\sqrt{2}\)
\(BC=\sqrt{\left(-1-2\right)^2+\left(2-4\right)^2}=\sqrt{13}\)
\(AC=\sqrt{\left(-1-1\right)^2+\left(2+3\right)^2}=\sqrt{29}\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+BC+AC=5\sqrt{2}+\sqrt{13}+\sqrt{29}\)
Xét ΔABC có
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
\(=\dfrac{50+29-13}{2\cdot5\sqrt{2}\cdot\sqrt{29}}=\dfrac{33}{5\sqrt{58}}\)
\(sin^2A+cos^2A=1\)
=>\(sin^2A=1-\left(\dfrac{33}{5\sqrt{58}}\right)^2=\dfrac{361}{1450}\)
=>\(sinA=\sqrt{\dfrac{361}{1450}}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=\dfrac{1}{2}\cdot\sqrt{\dfrac{361}{1450}\cdot50\cdot29}=\dfrac{19}{2}\)
b: Gọi (d): y=ax+b là phương trình đường thẳng AB
(d) đi qua A(1;-3) và B(2;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=-3\\2a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-a=-7\\a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=-3-a=-3-7=-10\end{matrix}\right.\)
Vậy: (d): y=7x-10
c: Gọi (d1):y=ax+b là phương trình đường thẳng cần tìm
Vì (d1) vuông góc AB nên \(a\cdot7=-1\)
=>\(a=-\dfrac{1}{7}\)
=>(d1): \(y=-\dfrac{1}{7}x+b\)
Thay x=-1 và y=2 vào (d1), ta được:
\(b+\dfrac{1}{7}=2\)
=>\(b=2-\dfrac{1}{7}=\dfrac{13}{7}\)
Vậy: (d1): \(y=-\dfrac{1}{7}x+\dfrac{13}{7}\)

b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)
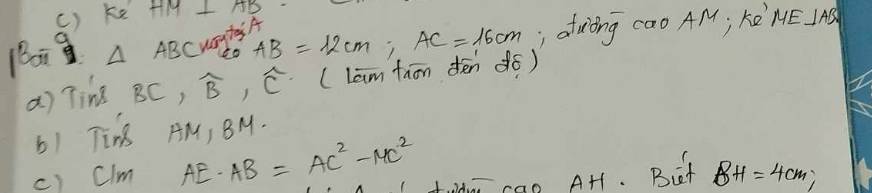
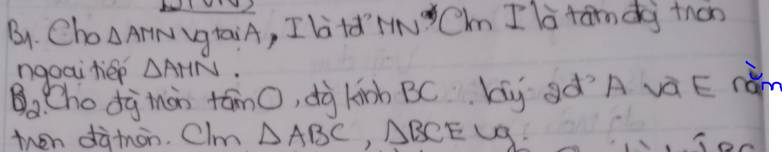
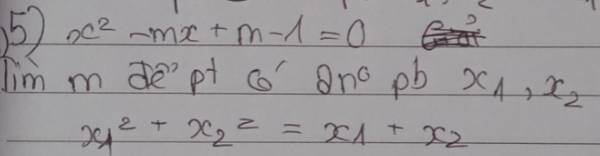
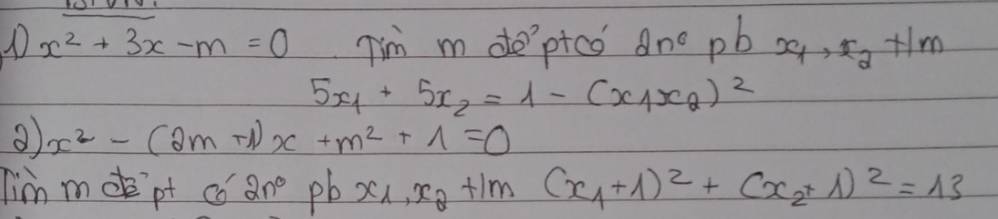
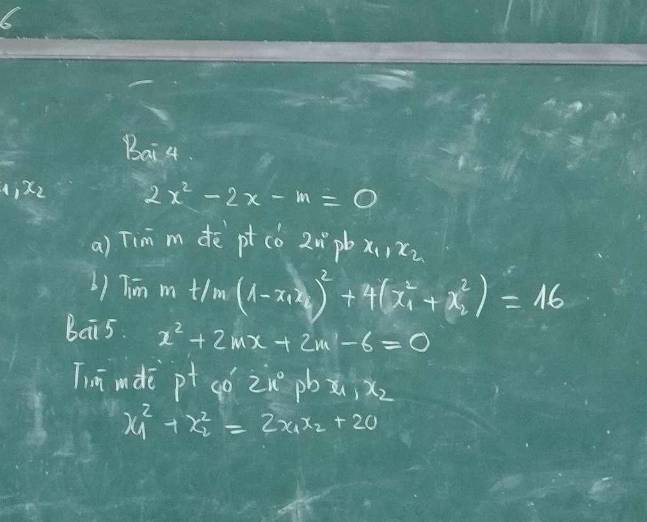
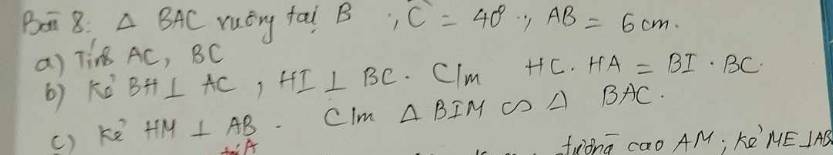
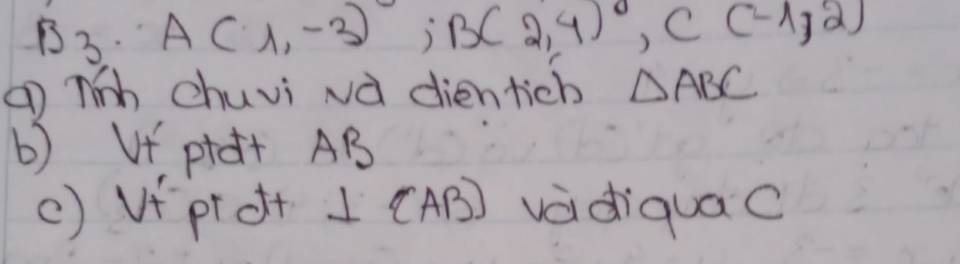

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AM là đường cao
nên \(\left\{{}\begin{matrix}AB\cdot AC=AM\cdot BC\\AB^2=BM\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AM=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\\BM=\dfrac{12^2}{20}=7.2\left(cm\right)\end{matrix}\right.\)
c: ΔABM vuông tại M có ME là đường cao
nên \(AE\cdot AB=AM^2\)
ΔAMC vuông tại M
=>\(MA^2+MC^2=AC^2\)
=>\(MA^2=AC^2-MC^2\)
=>\(AE\cdot AB=AC^2-MC^2\)