Câu 2:

a: Không

b: Không

Câu 3:

a: \(\widehat{B}=\widehat{zAB}\left(=124^0\right)\)

mà hai góc này là hai góc ở vị trí so le trong

nên Bt//Az

b: n\(\perp\)DC

m\(\perp\)DC

Do đó: n//m

c: \(\widehat{xEG}+\widehat{yGE}=70^0+110^0=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên Ex//Gy

d: Vẽ lại hình, ta sẽ có:

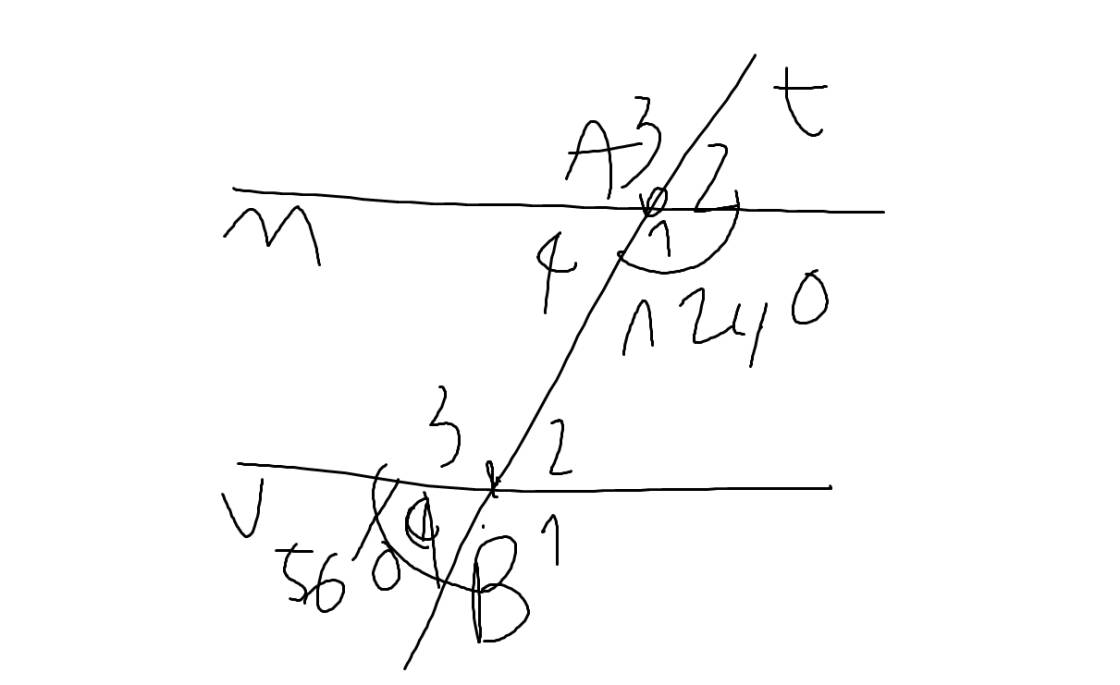
Ta có: \(\widehat{B_4}=\widehat{B_2}\)(hai góc đối đỉnh)

mà \(\widehat{B_4}=56^0\)

nên \(\widehat{B_2}=56^0\)

Ta có: \(\widehat{A_1}+\widehat{B_2}=124^0+56^0=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên m//v

a: MNPQ là hình bình hành

=>MQ//NP

=>MQ//IP

Xét tứ giác MIPQ có IP//MQ

nên MIPQ là hình thang

b: ΔMNP vuông cân tại N

=>MN=NP và \(\widehat{MNP}=90^0\)

Hình bình hành MNPQ có \(\widehat{MNP}=90^0\)

nên MNPQ là hình chữ nhật

=>\(\widehat{Q}=\widehat{P}=90^0\)

Xét ΔMNI vuông tại N có \(sinNMI=\dfrac{NI}{MN}=\dfrac{2}{3}\)

nên \(\widehat{NMI}\simeq42^0\)

\(\widehat{NMI}+\widehat{QMI}=\widehat{NMQ}=90^0\)

=>\(\widehat{QMI}+42^0=90^0\)

=>\(\widehat{QMI}=48^0\)

IP//MQ

=>\(\widehat{QMI}+\widehat{MIP}=180^0\)(hai góc trong cùng phía)

=>\(\widehat{MIP}+48^0=180^0\)

=>\(\widehat{MIP}=132^0\)

\(36x^2-25=\left(6x-5\right)\left(6x+5\right)\)

MK cảm thấy đề bài 1 cứ sai sai nhưng mk làm thử nhé

Bài 1. Gọi vận tốc xe từ A là x ( x > 0 , đơn vị : km/h )

Sau 2 giờ xe từ B đi được quãng đường là : 2.10 = 20 ( km )

Sau 2 giờ xe từ A đi được quãng đường là : 2x ( km)

Do 2 xe đi ngược chiều nhau nên đến khi gặp nhau tổng quãng đường hai xe đi bằng quãng đường AB , ta có phương trình sau :

2x + 20 = 180

⇔ 2x = 160

⇔ x = 80 ( thỏa mãn )

Vậy,....

Bài 2. Gọi quãng đường AB là x ( x > 0 , đơn vị : km)

Quãng đường đã đi trong 24 phút ( \(\dfrac{2}{5}\) giờ ) là : \(\dfrac{2}{5}\).50 = 20 ( km)

Quãng đường còn lại cần đi là : x - 20 ( km )

Thời gian đi với vận tốc 50km/h là : \(\dfrac{x}{50}\) ( giờ )

Thời gian đi với vận tốc 40km/h là : \(\dfrac{x-20}{40}\) ( giờ )

Đổi : 18 phút = \(\dfrac{3}{10}\) ( giờ )

Theo đề bài , ta có phương trình :

\(\dfrac{x}{50}\) + \(\dfrac{3}{10}\) = \(\dfrac{x-20}{40}\) + \(\dfrac{2}{5}\)

⇔\(\dfrac{x}{50}\) - \(\dfrac{x-20}{40}\) = \(\dfrac{2}{5}\) - \(\dfrac{3}{10}\)

⇔ \(\dfrac{4x-5x+100}{200}=\dfrac{1}{10}\)

⇔ \(\dfrac{100-x}{200}=\dfrac{1}{10}\)

⇔1000 - 10x = 200

⇔ 10x = 800

⇔ x = 80 ( thỏa mãn )

Vậy,....

bài 1

gọi thời gian đi từ A đến B là x(h;x>0)

nên vận tốc là 20x(km)

do thời gian lúc về nhiêu hơn lúc đi là 10'=\(\dfrac{1}{6}\) h

nên thời gian là x+\(\dfrac{1}{6}\left(h\right)\)

nên quãng đường là \(15\left(x+\dfrac{1}{6}\right)\) (km)

vì trên cùng 1 quãng đường nên ta có pt

\(20x=15\left(x+\dfrac{1}{6}\right)\)

⇔\(20x=15x+\dfrac{5}{2}\)

⇔20x-15x=\(\dfrac{5}{2}\)

⇔\(5x=\dfrac{5}{2}\)

⇔x=0,5(h)

Quãng đường AB là 20x=20.0,5=10(km)

vậy quãng đường AB là 10km

-Gọi t1 là thời gian của người đi xe đạp đi từ A đến B

-Gọi t2 là thời gian của người đi xe đạp đi từ B đến A

-do thời gian về hơn thời gian đi là 10 phút = \(\dfrac{1}{6}\)h

=> t2= t1 + \(\dfrac{1}{6}\)

-ta có: S1= v1 . t1 = 20t1

S2= v2 . t2 = 15.( t1 + \(\dfrac{1}{6}\))

-mà S1 = S2

=>20t1 = 15 ( t1 + \(\dfrac{1}{6}\))

<=>20t1=15t1 + 2,5

<=>20t1 - 15t1= 2,5

<=> 5t1 = 2,5

<=>t1=0,5

=> S1 = v1.t1=20 . 0,5=10

Vậy quãng đường AB dài 10km

tớ không biết dài quá

2,052641236x10^20

Bài 4

a) Do Cx // AB

⇒ ∠BCx = ∠ABC = 45⁰ (so le trong)

b) Do AB ⊥ AE

DE ⊥ AE

⇒ AB // DE

Mà Cx // AB

⇒ Cx // DE

c) Do Cx // DE

⇒ ∠DCx = ∠CDE = 60⁰ (so le trong)

⇒ ∠BCD = ∠BCx + ∠DCx

= 45⁰ + 60⁰

= 105⁰