
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1B:
a: Ta có: \(N=\sqrt{8}+\sqrt{32}+\sqrt{108}-\sqrt{27}\)
\(=2\sqrt{2}+4\sqrt{2}+6\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{2}+3\sqrt{3}\)
b: Ta có: \(M=\dfrac{2}{2+\sqrt{3}}-\dfrac{1}{2-\sqrt{3}}\)
\(=4-2\sqrt{3}-2-\sqrt{3}\)
\(=2-3\sqrt{3}\)

a: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔABC vuông tại C

2:
a: T=900-30c
b: giá trị của 900 thùng là:
900*2000000=1800000000(đồng)
Số tiền phải chi là:
900:30*2500000=75000000(đồng)
Xưởng sẽ lời khoảng:
1800000000-75000000=1725000000(đồng)

toán 9 mà sao câu 2a có giai thừa vậy bạn ??
chờ mình xíu nhé

1.
b, \(B=\dfrac{8+2\sqrt{2}}{3-\sqrt{2}}-\dfrac{2+3\sqrt{2}}{\sqrt{2}}+\dfrac{\sqrt{2}}{1-\sqrt{2}}\)
\(=\dfrac{2\left(2+\sqrt{2}\right)\left(3-\sqrt{2}\right)}{3-\sqrt{2}}-\dfrac{\sqrt{2}\left(\sqrt{2}+3\right)}{\sqrt{2}}+\dfrac{\sqrt{2}\left(1+\sqrt{2}\right)}{1-\sqrt{2}}\)
\(=4+2\sqrt{2}-\sqrt{2}-3-2-\sqrt{2}\)
\(=-1\)
Bài 1:
b: Ta có: \(B=\dfrac{8+2\sqrt{2}}{3-\sqrt{2}}-\dfrac{2+3\sqrt{2}}{\sqrt{2}}-\dfrac{\sqrt{2}}{\sqrt{2}-1}\)
\(=2\sqrt{2}\left(\sqrt{2}+1\right)-\sqrt{2}-3-2+\sqrt{2}\)
\(=4+2\sqrt{2}-5\)
\(=2\sqrt{2}-1\)

1b) \(C=\sqrt{81a}-\sqrt{144a}+\sqrt{36a}\left(a\ge0\right)=8\sqrt{a}-12\sqrt{a}+6\sqrt{a}=2\sqrt{a}\)
Bài 2:
a),b) \(P=\left(\dfrac{1}{1-\sqrt{a}}-\dfrac{1}{1+\sqrt{a}}\right)\left(\dfrac{1}{\sqrt{a}}+1\right)\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{1+\sqrt{a}-1+\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}.\dfrac{\sqrt{a}+1}{\sqrt{a}}=\dfrac{2\sqrt{a}}{1-\sqrt{a}}.\dfrac{1}{\sqrt{a}}=\dfrac{2}{1-\sqrt{a}}\)
c) \(P=\dfrac{2}{1-\sqrt{a}}=\dfrac{2}{1-\sqrt{4}}=\dfrac{2}{1-2}=-2\)
d) \(P=\dfrac{2}{1-\sqrt{a}}=9\)
\(\Rightarrow-9\sqrt{a}+9=2\Rightarrow\sqrt{a}=\dfrac{7}{9}\Rightarrow a=\dfrac{49}{81}\left(tm\right)\)

2b)
Áp dụng BĐT bunhiacopxki có:
\(\left(1+1\right)\left(x^4+y^4\right)\ge\left(x^2+y^2\right)^2\)
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2\)\(\Leftrightarrow x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}\)
\(\Rightarrow2\left(x^4+y^4\right)\ge\dfrac{\left(x+y\right)^4}{4}\Leftrightarrow x^4+y^4\ge\dfrac{1}{8}.\left(x+y\right)^4\)
Dấu "=" xảy ra khi x=y
3)
Áp dụng bđt Holder có:
\(\left(x^3+y^3+z^3\right)\left(1+1+1\right)\left(1+1+1\right)\ge\left(x+y+z\right)^3\)
\(\Leftrightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\)
Dấu "=" xảy ra khi x=y=z
3)(Nếu không dùng Holder)
Với x,y,z >0, ta có bđt sau:\(2x^3+2y^3+2z^3\ge xy\left(x+y\right)+yz\left(y+z\right)+xz\left(x+z\right)\) (1)
Thật vậy (1)\(\Leftrightarrow\left(x+y\right)\left(x^2-xy+y^2\right)-xy\left(x+y\right)+\left(y+z\right)\left(y^2-yz+z^2\right)-yz\left(y+z\right)+\left(z+x\right)\left(z^2-zx+x^2\right)-zx\left(x+z\right)\ge0\)
\(\Leftrightarrow\left(x+y\right)\left(x-y\right)^2+\left(y+z\right)\left(y-z\right)^2+\left(z+x\right)\left(z-x\right)^2\ge0\) (lđ)
Áp dụng AM-GM có:
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow\dfrac{2\left(x^3+y^3+z^3\right)}{3}\ge2xyz\) (2)
Từ (1) và (2), cộng vế với vế \(\Rightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge xy\left(x+y\right)+yz\left(x+z\right)+xz\left(x+z\right)+2xyz\)
\(\Leftrightarrow\dfrac{8}{3}\left(x^3+y^3+z^3\right)\ge\left(x+y\right)\left(y+z\right)\left(z+x\right)\)
\(\Leftrightarrow8\left(x^3+y^3+z^3\right)\ge3\left(x+y\right)\left(y+z\right)\left(x+z\right)\)
\(\Leftrightarrow9\left(x^3+y^3+z^3\right)\ge x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(z+x\right)=\left(x+y+z\right)^3\)
\(\Rightarrow x^3+y^3+z^3\ge\dfrac{1}{9}\left(x+y+z\right)^3\) (đpcm)

\(\Delta=\left(-m\right)^2-4\left(2m-4\right)\)
\(=m^2-8m+16\)
\(=\left(m-4\right)^2>0\) khi \(m\ne4\)





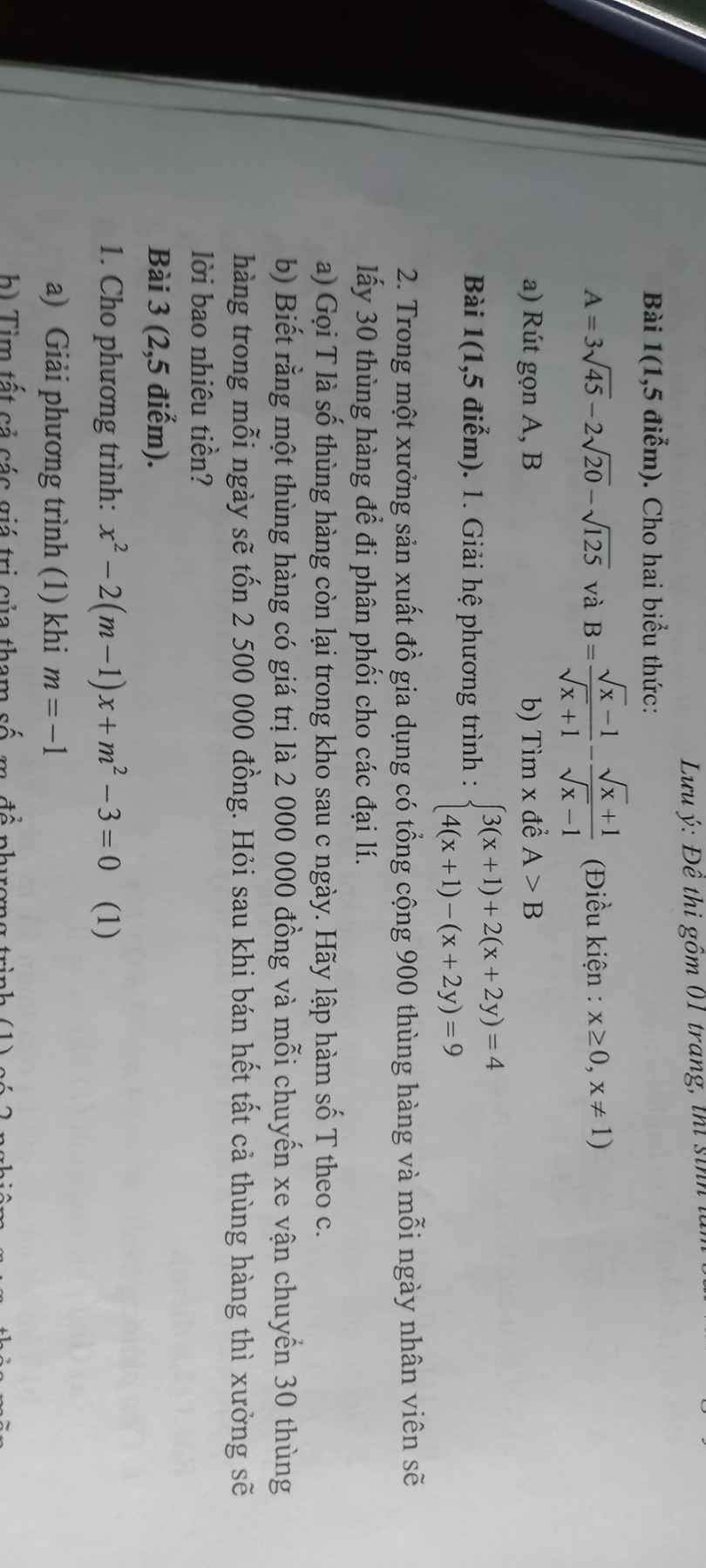



 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ
Bài 1b
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=BH.CH\Rightarrow CH=x=\frac{AH^2}{BH}=\frac{25}{4}\)cm
=> \(BC=BH+x=4+\frac{25}{4}=\frac{41}{4}\)cm
* Áp dụng hệ thức : \(AC^2=CH.BC=\frac{25}{4}.\frac{41}{4}=\frac{1025}{16}\Rightarrow AC=y=\frac{5\sqrt{41}}{4}\)cm