Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) xét tg ABD và tg ACD có :
AB = AC (gt)
AD chung
Góc BAC = góc DAC( AD là p/g góc BAC)
=> tg ABD = tg ADC( c-g-c)
b)xét tg AMB và tg AMC có:
AM chung
AB = AC (gt)
góc BAM = góc CAM ( M thuộc AD)
=> tg ABM = tg ACM ( c-g-c)
c)vì tg ADB = tg ADC (cmt)
=> DB = DC (cạnh tương ứng )
Vì tg AMB = tg AMC (cmt)
=> BM = MC (cạnh tương ứng)
Xét tg MBD và tg MCD có
MB= MC (cmt)
MD chung
BD = DC ( cmt)
=> tg MBD = tg MCD ( c-c-c)

a, Ta co góc BAD + góc ADC = 180 độ
mà góc ở vị trí trong cùng phía
=> AB//DC
b, Ta có góc ABC + góc xBC = 180 độ ( kề bù)
=> góc ABC = 180 - góc xBC = 180 -32 =148 độ
Ta có AB // DC hay Ax//DC
=> góc xBC = góc BCD = 32 độ ( sole trong)
a, Ta có \(\widehat{BAD}\) + \(\widehat{ADC}\) = 180 độ
mà 2 góc này ở vị trí trong cùng phía của AD cắt AB và CD
=> AB//DC
b, Ta có \(\widehat{ABC}\) + \(\widehat{xBC}\) = 180 độ ( kề bù)
=> \(\widehat{ABC}\) = 180 - \(\widehat{xBC}\) = 180 -32 =\(148^0\)
Ta có AB // DC hay Ax//DC
=> \(\widehat{xBC}\) = \(\widehat{BCD}\) = \(32^0\) ( so le trong)

3.14:
Ta thấy $\widehat{xNM}=\widehat{xQP}=45^0$. Mà 2 góc này ở vị trí đồng vị nên $MN\parallel PQ$
3.15
$EF\parallel NP$ do cùng vuông góc với $MH$
3.16: Bạn tự vẽ hình nhé.
3.17:
Ta thấy $\widehat{yKH}+\widehat{KHx}=130^0+50^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $Ky\parallel Hx$

\(x=\left(\dfrac{1}{2}\right)^3:\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^{3-1}=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)

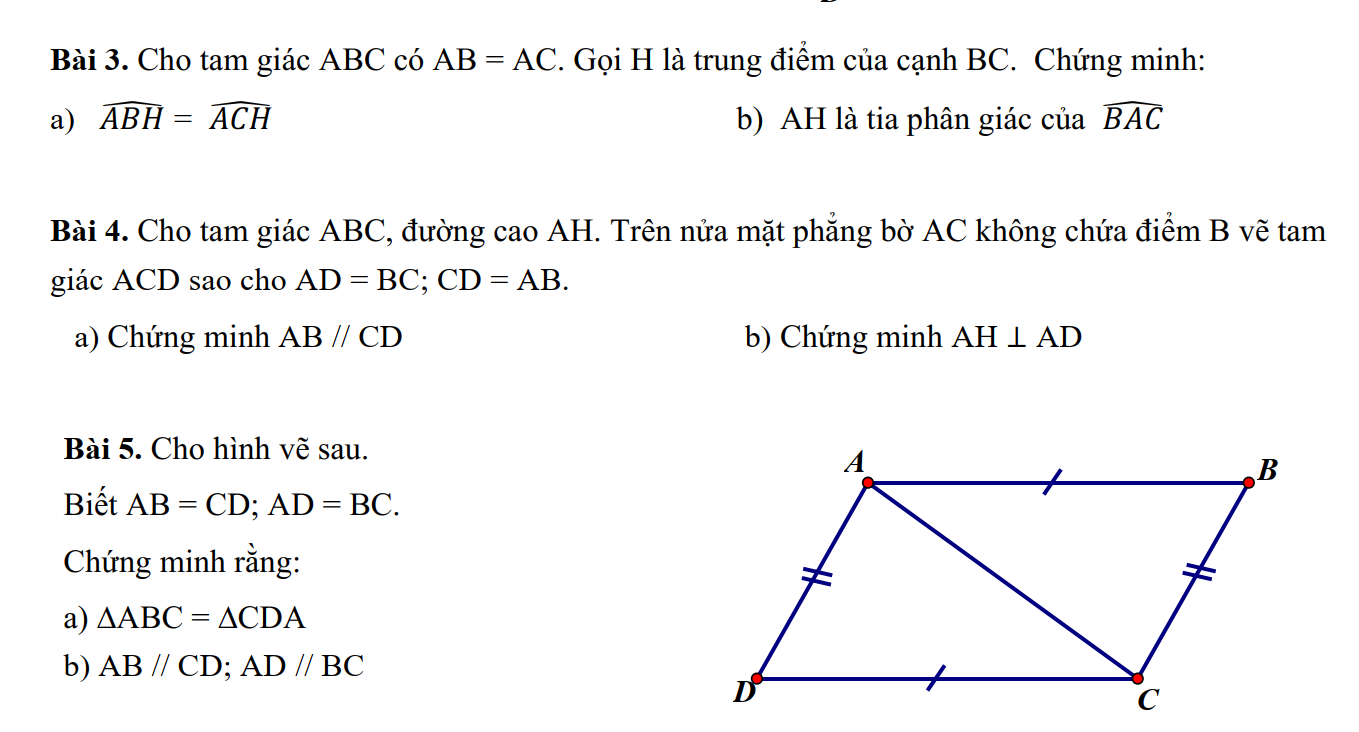
\(5,\\ a,\left\{{}\begin{matrix}AB=CD\left(gt\right)\\AD=BC\left(gt\right)\\AC.chung\end{matrix}\right.\Rightarrow\Delta ABC=\Delta CDA\left(c.c.c\right)\\ b,\Delta ABC=\Delta CDA\left(cm.trên\right)\\ \Rightarrow\left\{{}\begin{matrix}\widehat{CAB}=\widehat{DCA}\\\widehat{CAD}=\widehat{ACB}\end{matrix}\right.\left(các.cặp.góc.tương.ứng\right)\)
Mà các cặp góc này ở vị trí so le trong nên \(AB//CD;AD//BC\)

`#040911`
`3.11`
Vì \(\widehat{x'AB}=\widehat{ABy}=60^0\)
Mà `2` góc này nằm ở vị trí sole trong
`=>` \(xx'\text {//}yy'\) `(\text {tính chất 2 đt' //})`
`3.12`
Vì \(\left\{{}\begin{matrix}\text{HK }\bot\text{ }a\\\text{HK }\bot\text{ }b\end{matrix}\right.\)
`=> \text {a // b} (\text {tính chất 2 đt' //}).`








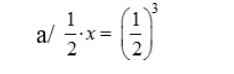 giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn
giúp em bài này với ạ,giải chi tiết luôn nha,em cảm ơn