
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đài ơi, giải giúp cho Sarah đi, tớ không có viết và giờ vào giường rồi , good nigh

Câu 13:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM\cdot6=3,6^2\)
=>BM=2,16(cm)
Xét ΔHAC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\)
=>\(AN\cdot8=4,8^2\)
=>AN=2,88(cm)
ΔABN vuông tại A
=>\(AB^2+AN^2=BN^2\)
=>\(BN^2=2.88^2+6^2=44,2944\)
=>\(BN=\sqrt{44,2944}=\dfrac{6\sqrt{769}}{25}\left(cm\right)\)
Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>AH=MN=4,8(cm)
Xét ΔMBN có \(cosBMN=\dfrac{MB^2+MN^2-NB^2}{2\cdot MB\cdot MN}\)
\(=\dfrac{4,8^2+2,16^2-\dfrac{27684}{625}}{2\cdot4,8\cdot2,16}=\dfrac{-10368}{625}:\dfrac{2592}{125}=-\dfrac{4}{5}\)
=>\(sinBMN=\sqrt{1-\left(-\dfrac{4}{5}\right)^2}=\dfrac{3}{5}\)
Xét ΔBMN có \(\dfrac{NB}{sinBMN}=2R\)
=>\(2R=\dfrac{6\sqrt{769}}{25}:\dfrac{3}{5}=\dfrac{6\sqrt{769}}{25}\cdot\dfrac{5}{3}=\dfrac{2}{5}\sqrt{769}\)
=>\(R=\dfrac{\sqrt{769}}{5}\)
=>Chọn A

b: Tọa độ là:
\(\left\{{}\begin{matrix}\dfrac{2}{3}x=-\dfrac{1}{3}x+2\\y=\dfrac{2}{3}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{4}{3}\end{matrix}\right.\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{2}{3}x=-\dfrac{1}{3}x+2\\y=\dfrac{2}{3}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{4}{3}\end{matrix}\right.\)

a,
c, Gọi \(\left(D_3\right):y=ax+b\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}a=-2;b\ne0\\3x+3=ax+b,\forall x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\-a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-2\end{matrix}\right.\)
Vậy \(\left(D_3\right):y=-2x-2\)

Chắc chắn đây là bài thi, hình như là bạn ý dùng màu đen để che điểm.
Câu 1
a) Đất trồng là gì?
b) Đất có vai trò đặc biệt như thế nào đối với đời sống cây trồng?
a) Trả lời: Là bề mặt tơi xốp của vỏ Trái Đất, trên đó thực vật có khả năng sinh sống và sản xuất ra sản phẩm.
b) Trả lời: Là môi trường cung cấp nước, chất dinh dưỡng, oxi cho cây và giúp cho cây đứng vững.
Câu 2. Em hãy nêu thành phần của đất trồng?
Trả lời Đất trồng gồm 3 phần: khí, lỏng, rắn
Câu 3. Em hãy nêu các biện pháp cải tạo đất?
Trả lời Cày sâu, bừa kĩ, bón phân hữu cơ
- Làm ruộng bậc thang
- Trồng xen cây nông nghiệp giữa các băng cây phân xanh
- Cày nông, bừa sục, giữ nước liên tục, thay nước thường xuyên
- Bón vôi.
Câu 4
a) Em hãy nêu những dấu hiệu thường gặp ở cây khi bị sâu, bệnh phá hại?
b) Em hãy nêu tác hại của sâu bệnh?
a) Trả lời : Thường có những biến đổi về màu sắc, hình thái, cấu tạo...
b) Trả lời: Sâu bệnh có những ảnh hưởng xấu đến đời sống cây trồng. Khi bị sâu, bệnh phá hại, cây trồng sinh trưởng, phát triển kém, năng suất và chất lượng nông sản giảm, thậm chí không cho thu hoạch.


Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)

c: \(\sqrt{3+\sqrt{8}}=\sqrt{2}+1\)
d: \(\sqrt{11+4\sqrt{6}}=2\sqrt{2}+3\)
e: \(\sqrt{14-6\sqrt{5}}=3-\sqrt{5}\)


 câu 13, 14, 15 ạ giúp em với
câu 13, 14, 15 ạ giúp em với





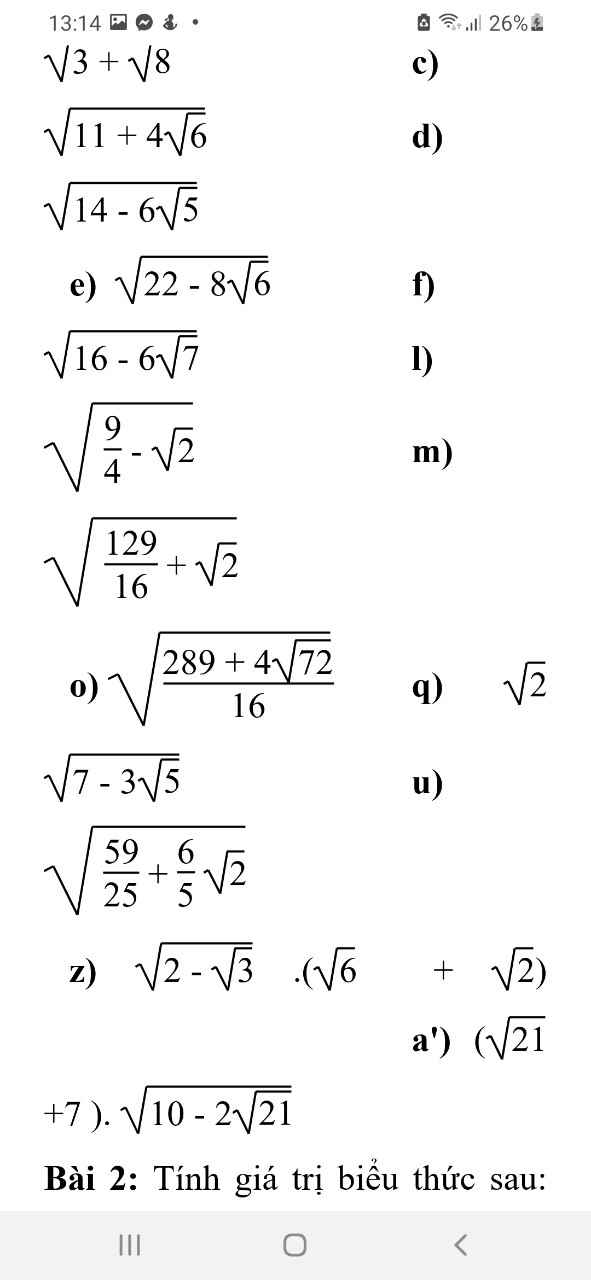
Lời giải:
Gọi $O$ là giao điểm của $AC, BD$. Vì $AC\perp BD$ nên $AOB, AOD, DOC, BOC$ là tam giác vuông tại $O$.
Do đó, áp dụng định lý Pitago cho các tam giác trên thì:
$AD^2=AO^2+OD^2$
$BC^2=BO^2+OC^2$
$\Rightarrow AD^2+BC^2=OA^2+OB^2+OC^2+OD^2(1)$
$AB^2=AO^2+OB^2$
$CD^2=DO^2+CO^2$
$\Rightarrow AB^2+CD^2=OA^2+OB^2+OC^2+OD^2(2)$
Từ $(1);(2)\Rightarrow AD^2+BC^2=AB^2+CD^2$
Ta có đpcm.
Hình vẽ:
