ko có biết

b: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có 

\(\widehat{ABH}\) chung

Do đó: ΔAHB\(\sim\)ΔCAB

Suy ra: \(\dfrac{AB}{CB}=\dfrac{HB}{AB}\)

hay \(AB^2=BH\cdot BC\)

Lời giải:
a. $(x^2-1)(x^2+2x)=x^4+2x^3-x^2-2x$

b. $(2x-1)(3x+2)(3-x)=(6x^2+4x-3x-2)(3-x)$

$=(6x^2+x-2)(3-x)=18x^2-6x^3+3x-x^2-6+2x$

$=-6x^3+17x^2+5x-6$

c.

$(x+3)(x^2+3x-5)=x^3+3x^2-5x+3x^2+9x-15$

$=x^3+6x^2+4x-15$

d.

$(x+1)(x^2-x+1)=x^3+1^3=x^3+1$

e.

$(2x^3-3x-1)(5x+2)=10x^4+4x^3-15x^2-6x-5x-2$

$=10x^4+4x^3-15x^2-11x-2$

f.

$(x^2-2x+3)(x-4)=x^3-4x^2-2x^2+8x+3x-12$

$=x^3-6x^2+11x-12$
 

Bài 5:

\(a,\dfrac{2}{2x-4}=\dfrac{2}{2\left(x-2\right)}=\dfrac{1}{x-2};\dfrac{3}{3x-6}=\dfrac{3}{3\left(x-2\right)}=\dfrac{1}{x-2}\\ b,\dfrac{1}{x+4}=\dfrac{2\left(x-4\right)}{2\left(x+4\right)\left(x-4\right)};\dfrac{1}{2x+8}=\dfrac{x-4}{2\left(x+4\right)\left(x-4\right)}\\ \dfrac{3}{x-4}=\dfrac{6\left(x+4\right)}{2\left(x-4\right)\left(x+4\right)}\\ c,\dfrac{1}{x^2-1}=\dfrac{1}{\left(x-1\right)\left(x+1\right)};\dfrac{2}{x-1}=\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}\\ \dfrac{2}{x+1}=\dfrac{2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\\ d,\dfrac{1}{2x}=\dfrac{x-2}{2x\left(x-2\right)};\dfrac{2}{x-2}=\dfrac{4x}{2x\left(x-2\right)};\dfrac{3}{2x\left(x-2\right)}\text{ giữ nguyên}\)

Bài 4:

\(a,\dfrac{x^2-4x+4}{x^2-2x}=\dfrac{\left(x-2\right)^2}{x\left(x-2\right)}=\dfrac{x-2}{x}=\dfrac{\left(x-2\right)\left(x-1\right)}{x\left(x-1\right)}\\ \dfrac{x+1}{x^2-1}=\dfrac{1}{x-1}=\dfrac{x}{x\left(x-1\right)}\\ b,\dfrac{x^3-2^3}{x^2-4}=\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+2x+4}{x+2};\dfrac{3}{x+2}\text{ giữ nguyên}\)

Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN

Ta có: \(x^2+2\ge0\forall x\)

\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)

Vậy GTLN của A là 1/2

=> A

Câu 2: B đạt GTLN khi và chỉ khi x² đạt giá trị nhỏ nhất

⇔ x²=0 ⇒B = 10 - 0= 0 

  Chọn đáp án B nhe

Câu 3: Có A= 4x - 2x²= (-2x² + 4x - 1) + 1=\(-2\left(x^2-2x+1\right)+1\)

⇔ A= \(-2\left(x-1\right)^2+1\le1\)

Chọn đáp án B nha

Câu 4: 

a: Ta có: \(A=\left(4x+1\right)\left(4x-1\right)+2\left(x-1\right)^2-2\left(3x-2\right)^2\)

\(=16x^2-1+2x^2-4x+2-2\left(9x^2-12x+4\right)\)

\(=18x^2-4x+1-18x^2+24x-8\)

\(=20x-7\)

b: Để A=3 thì 20x-7=3

hay \(x=\dfrac{1}{2}\)

Câu 5:

a: Ta có: \(AM=MB=\dfrac{AB}{2}\)

\(AD=BC=\dfrac{AB}{2}\)

\(DN=NC=\dfrac{DC}{2}\)

mà AB=DC

nên AM=MB=CB=NC=ND=AD

Xét ΔAND có AD=DN

nên ΔAND cân tại D

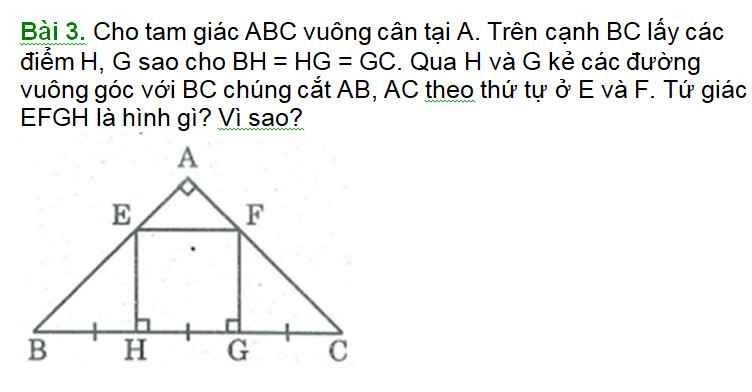
Xét tứ giác EHGF có:

EH//GF(cùng vuôn góc BC)

\(\widehat{EHG}=90^0\)(EH⊥HG)

=> EHGF là hình chữ nhật(1)

Xét tam giác EBG có:

EH là đường cao(EH⊥BG)

EH là trung tuyến(BH=HG)

=> Tam giác EBG cân tại E

Mà \(\widehat{EBH}=45^0\)(ABC vuông cân tại A)

=> Tam giác EBG vuông cân tại E

=> \(EH=\dfrac{1}{2}BG=HG\left(2\right)\)(EH là trung tuyến ứng với cạnh huyền)

\(\left(1\right),\left(2\right)\Rightarrow\) EHGF là hình vuông

Em cảm ơn ạ