
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$y-x^2y-2xy^2-y^3=y(1-x^2-2xy-y^2)$
$=y[1-(x^2+2xy+y^2)]=y[1-(x+y)^2]=y(1-x-y)(1+x+y)$

a) x^2 - x = 0
x(x-1)=0
x=0 hoặc x=1
b) (x-2)^2 - 3(x-2)=0
(x-2)(x-5)=0
x=2 hoặc x=5
c) pt <=> 3(x - 1) - 2(x - 1)=0
<=> x-1=0
<=> x = 1
a) \(\Rightarrow x\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
b) \(\Rightarrow\left(x-2\right)\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
c) \(\Rightarrow3\left(x-1\right)-2\left(x-1\right)=0\)
\(\Rightarrow x-1=0\Rightarrow x=1\)
d) \(\Rightarrow\left(x-5\right)\left(x+5\right)+\left(x-5\right)^2=0\)
\(\Rightarrow\left(x-5\right).2x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
e) \(\Rightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

e) Ta có: \(x^3-4x-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2\right)-14x\left(x-2\right)=0\)
\(\Leftrightarrow x\left(x-2\right)\left(x+2-14\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=12\end{matrix}\right.\)
e)x3-4x+14x(x-2)=0
⇔ x(x2-4)+14x(x-2)=0
⇔ x(x-2)(x+2)+14x(x-2)=0
⇔ (x-2)(x2+2x+14x)=0
⇔ x(x-2)(x+16)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-2=0\\x+16=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\\x=-16\end{matrix}\right.\)
g)x2(x+1)-x(x+1)+x(x-1)=0
⇔ (x+1)(x2-x)+x(x-1)=0
⇔ x(x+1)(x-1)+x(x-1)=0
⇔ x(x-1)(x+2)=0
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=1\\x=-2\end{matrix}\right.\)

\(8,=\left(2x-3\right)\left(2x+3\right)\\ 9,=\left(1-5a^2\right)\left(1+5a^2\right)\)
8) \(-9+4x^2=\left(2x\right)^2-3^2=\left(2x-3\right)\left(2x+3\right)\)
9) \(1-25a^4=1-\left(5a^2\right)^2=\left(1-5a^2\right)\left(1+5a^2\right)\)

a) \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}\\\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{15}=\dfrac{z}{21}\end{matrix}\right.\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x+y+z}{10+15+21}=\dfrac{92}{46}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{10}=2\Rightarrow x=2.10=20\\\dfrac{y}{15}=2\Rightarrow y=2.15=30\\\dfrac{z}{21}=2\Rightarrow z=2.21=42\end{matrix}\right.\)

\(B=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(B_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(C=\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\)
\(C_{min}=2\) khi \(\left(x;y\right)=\left(1;2\right)\)
b) Ta có: \(B=\left(x-1\right)\left(x+2\right)\left(x+3\right)\left(x+6\right)\)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\forall x\)
Dấu '=' xảy ra khi x(x+5)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy: \(B_{min}=-36\) khi \(x\in\left\{0;-5\right\}\)
c) Ta có: \(C=x^2-2x+y^2-4y+7\)
\(=x^2-2x+1+y^2-4y+4+2\)
\(=\left(x-1\right)^2+\left(y-2\right)^2+2\ge2\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
Vậy: \(C_{min}=2\) khi (x,y)=(1;2)

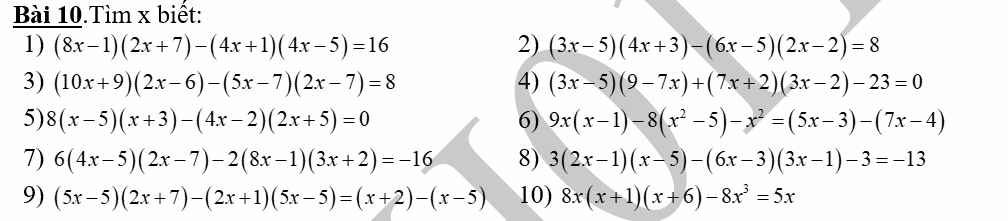 giúp em câu 6,9,10 câu này khó em k làm dc
giúp em câu 6,9,10 câu này khó em k làm dc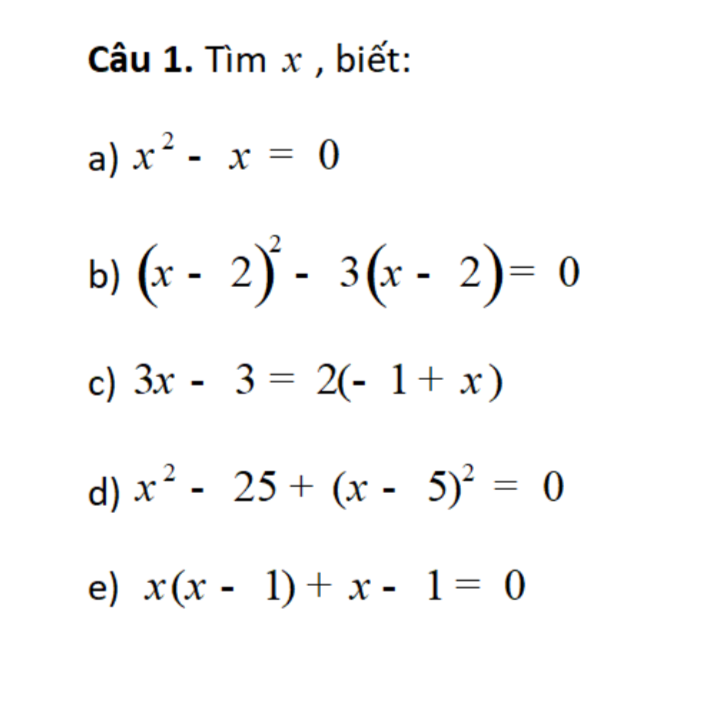
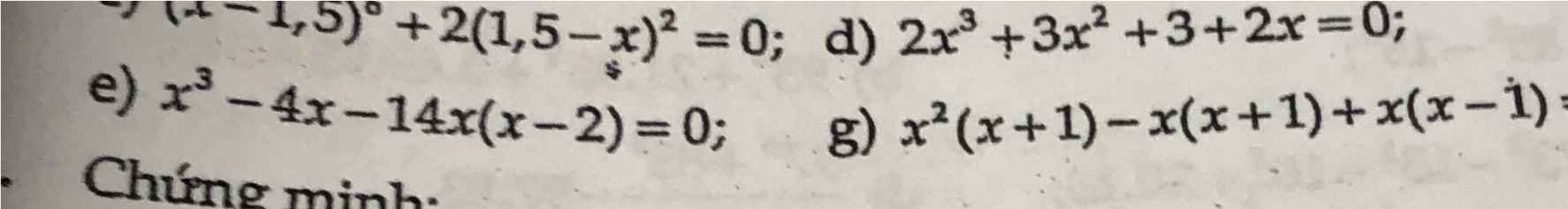


 Câu d khá khó mn giúp em với
Câu d khá khó mn giúp em với


\(5,\Leftrightarrow8\left(x^2-5x+3x-15\right)-\left(8x^2-4x+20x-10\right)=0\)
\(\Leftrightarrow8x^2-40x+24x-120-8x^2+4x-20x+10=0\)
\(\Leftrightarrow-32x-110=0\)
\(\Leftrightarrow x=\dfrac{110}{-32}=-\dfrac{55}{16}\)
\(9,\Leftrightarrow\left(5x-5\right)\left(2x+7-2x-1\right)=x+2-x+5\)
\(\Leftrightarrow6\left(5x-5\right)=7\)
\(\Leftrightarrow5x-5=\dfrac{7}{6}\)
\(\Leftrightarrow x=\dfrac{37}{30}\)
\(8,\Leftrightarrow\left(6x-3\right)\left(x-5-3x+1\right)-3+13=0\)
\(\Leftrightarrow-6\left(2x-1\right)\left(x+2\right)+10=0\)
\(\Leftrightarrow2x^2-x+4x-2=\dfrac{10}{6}\)
\(\Leftrightarrow2x^2+3x-\dfrac{11}{3}=0\)
\(10,\Leftrightarrow8x\left(x^2+x+6x+6\right)-8x^3=5x\)
\(\Leftrightarrow8x^3+8x^2+48x^2+48x-8x^3-5x=0\)
\(\Leftrightarrow56x^2+43x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{43}{56}\end{matrix}\right.\)
Vậy ....
;-; quên đọc đề may làm trúng 9; 10 câu 6 nốt đây nha
\(6,\Leftrightarrow9x^2-9x-8x^2+40-x^2=5x-3-7x+4\)
\(\Leftrightarrow9x^2-9x-8x^2+40-x^2-5x+3+7x-4=0\)
\(\Leftrightarrow-7x+39=0\)
\(\Leftrightarrow x=\dfrac{39}{7}\)
Vậy ...