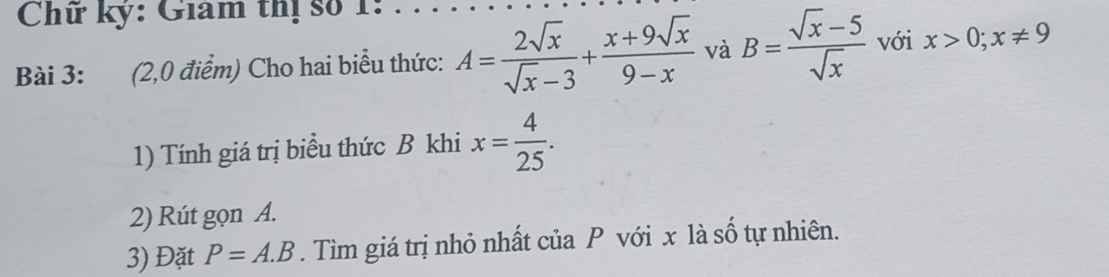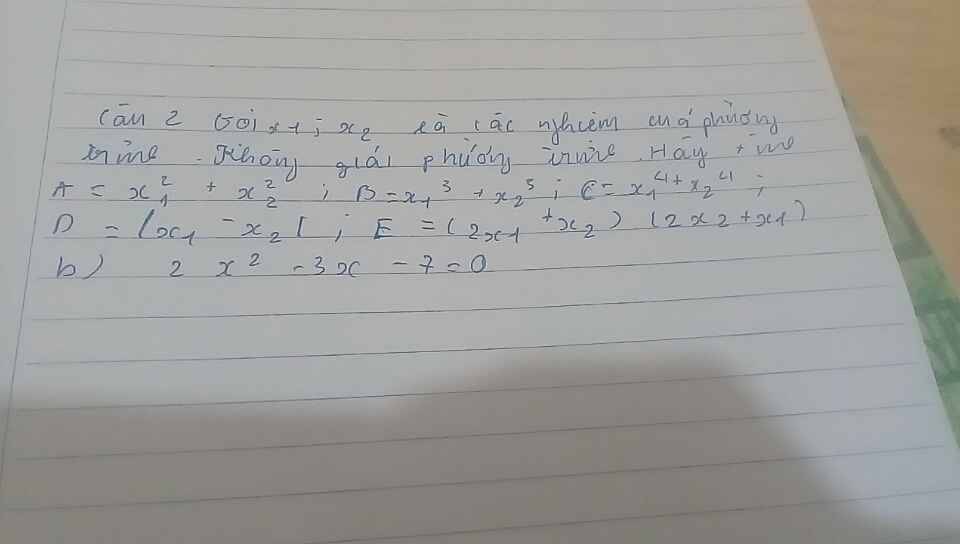b: ĐKXĐ: x<=5

d: DKXĐ: x<=5/3

135

g: \(\text{Δ}=\left(-6\right)^2-4\left(2m+1\right)=36-8m-4=-8m+32\)

Để phương trình có hai nghiệm thì -8m+32>=0

=>m<=4

Để phương trình có hai nghiệm cùng âm thì:

\(\left\{{}\begin{matrix}m< =4\\\dfrac{-\left(-6\right)}{1}< 0\\2m+1>0\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

h: \(\left\{{}\begin{matrix}2x_1-x_2=15\\x_1+x_2=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=7\\x_2=-1\end{matrix}\right.\)

x1*x2=2m+1

=>2m+1=-7

=>2m=-8

=>m=-4

i: \(x_1^2+x_2^2=5\)

=>(x1+x2)^2-2x1x2=5

=>6^2-2(2m+1)=5

=>36-4m-2=5

=>34-4m=5

=>4m=29

=>m=29/4(loại)

j: \(x_1^3+x_2^3=5\)

=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=5\)

=>\(6^3-3\cdot6\cdot\left(2m+1\right)=5\)

=>216-18(2m+1)=5

=>18(2m+1)=211

=>2m+1=211/18

=>2m=193/18

=>m=193/36(loại)

A=P^2-P

\(=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-2\right)^2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)

\(=\dfrac{x+2\sqrt{x}+1-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)^2}=\dfrac{3\sqrt{x}+3}{\left(\sqrt{x}-2\right)^2}>=0\)

=>P^2>=P

Xin lỗi nha, mình ko biết vẽ hình trên máy nên bạn tự vẽ hình giùm mình nha

b)Ta có:\(\widehat{MNB}=\dfrac{1}{2}\stackrel\frown{BM}\left(1\right)\)( góc nội tiếp chắn cung BM)

\(\widehat{AEB}=\dfrac{1}{2}\left(\stackrel\frown{AB-\stackrel\frown{AM}}\right)\)= \(\dfrac{1}{2}\stackrel\frown{BM}\)(2) (Góc có đỉnh ngoài đường tròn)

Từ (1) và (2) ⇒ \(\widehat{MNB}=\widehat{AEB}\)

Xét Δ BMN và Δ BFE có:

\(\widehat{B}\): góc chung

\(\widehat{MNB}=\widehat{AEB}\) ( cùng chắn \(\stackrel\frown{BM}\) )

Do đó: Δ BMN \(\sim\) Δ BFE(g-g)

⇔ BM . BE =BN . BF (đpcm)

vẽ giùm cái hình đi, lười vẽ hình trên này quá

Đợi ngày này 4 năm nữa em giải cho

1) \(B=\dfrac{\sqrt{x}-5}{\sqrt{x}}\)

Thay \(x=\dfrac{4}{25}\) vào B, ta được:

\(B=\dfrac{\sqrt{\dfrac{4}{25}}-5}{\sqrt{\dfrac{4}{25}}}\)

\(=\dfrac{\dfrac{2}{5}-5}{\dfrac{2}{5}}\)

\(=\dfrac{-\dfrac{23}{5}}{\dfrac{2}{5}}\)

\(=-\dfrac{23}{2}\)

2) ĐKXĐ: \(x\ne9;x\ge0\)

\(A=\dfrac{2\sqrt{x}}{\sqrt{x}-3}+\dfrac{x+9\sqrt{x}}{9-x}\)

\(=\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{x+9\sqrt{x}}{x-9}\)

\(=\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{2x+6\sqrt{x}-x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)

3) \(P=A.B\)

\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}.\dfrac{\sqrt{x}-5}{\sqrt{x}}\)

\(=\dfrac{\sqrt{x}-5}{\sqrt{x}+3}\)

\(=\dfrac{\sqrt{x}+3-8}{\sqrt{x}+3}\)

\(=1-\dfrac{2}{\sqrt{x}+3}\)

Để P nhỏ nhất thì \(\dfrac{8}{\sqrt{x}+3}\) lớn nhất

Ta có:

\(\dfrac{8}{\sqrt{x}+3}\ge\dfrac{8}{3}\)

\(\Rightarrow P\) nhỏ nhất là \(1-\dfrac{8}{3}=-\dfrac{5}{3}\) khi \(x=0\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{3}{2}\\x_1x_2=-\dfrac{7}{2}\end{matrix}\right.\)

\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\dfrac{37}{4}\)

\(B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\dfrac{153}{8}\)

\(C=x_1^4+x_2^4=\left(x_1^2+x_2^2\right)^2-2\left(x_1x_2\right)^2=\dfrac{977}{16}\)

\(D=\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\dfrac{\sqrt{65}}{2}\)

\(E=\left(2x_1+x_2\right)\left(2x_2+x_1\right)=2\left(x_1^2+x_2^2\right)+5x_1x_2=1\)