
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Vì D,M là trung điểm AB,AC nên DM là đtb tg ABC
Do đó \(DM=\dfrac{1}{2}BC=\dfrac{7}{2}\left(cm\right)\) và DM//BC


5:
\(\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}>=3\cdot\sqrt[3]{\dfrac{a}{b}\cdot\dfrac{b}{c}\cdot\dfrac{c}{a}}=3\)
a^2+b^2>=2ab
b^2+c^2>=2bc
a^2+c^2>=2ac
=>a^2+b^2+c^2>=ab+bc+ac
=>(ab+bc+ac)/(a^2+b^2+c^2)>=1
=>a/b+b/c+c/a+(ab+ac+bc)/(a^2+b^2+c^2)>=4

a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)

a: \(A=\dfrac{2x^2+x^2-1-2x^2+2x+1}{x\left(x+1\right)}=\dfrac{x^2+2x}{x\left(x+1\right)}=\dfrac{x+2}{x+1}\)
b: Ta có: \(x^2-2x=0\)
=>x=2
Thay x=2 vào A, ta được:
\(A=\dfrac{2+2}{2+1}=\dfrac{4}{3}\)
(a)
\(A=\dfrac{2x}{x+1}+\dfrac{x-1}{x}-\dfrac{2x^2-2x-1}{x^2+x}\\ =\dfrac{2x}{x+1}+\dfrac{x-1}{x}-\dfrac{2x^2-2x-1}{x\left(x+1\right)}=\dfrac{2x^2}{x\left(x+1\right)}+\dfrac{x^2-1}{x\left(x+1\right)}-\dfrac{2x^2-2x-1}{x\left(x-1\right)}\)
\(=\dfrac{2x^2+x^2-1-2x^2+2x+1}{x\left(x+1\right)}=\dfrac{x^2+2x+1}{x\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+1\right)}{x\left(x+1\right)}=\dfrac{x+1}{x}\)
(b)
\(x^2-2x=0\\ x\left(x-2\right)=0\)
=>x=0 hoặc x=2 mà đk x khác 0 nên thay x=2 vào bt A , ta có:
\(\dfrac{x+1}{x}=\dfrac{2+1}{2}=\dfrac{3}{2}\)


1: \(\dfrac{11}{x^4y};\dfrac{3}{xy^3}\)
\(\dfrac{11}{x^4y}=\dfrac{11\cdot y^2}{x^4y^3}=\dfrac{11y^2}{x^4y^3}\)
\(\dfrac{3}{xy^3}=\dfrac{3\cdot x^3}{xy^3\cdot x^3}=\dfrac{3x^3}{x^4y^3}\)
2: \(\dfrac{2}{3x^3y^2};\dfrac{3}{4x^7y}\)
\(\dfrac{2}{3x^3y^2}=\dfrac{2\cdot4\cdot x^4}{3x^3y^2\cdot4x^4}=\dfrac{8x^4}{12x^7y^2}\)
\(\dfrac{3}{4x^7y}=\dfrac{3\cdot3\cdot y}{4x^7y\cdot3y}=\dfrac{9y}{12x^7y^2}\)

Bài 4:
\(A=2x^2+3x-10x-15-2x^2+6x+x+7=-8\\ B=x^3-y^3-5+2y^3-x^3-y^3=-5\\ C=x^3-3x^2+3x-1-x^3-3x^2-3x-1-6x^2+6=4\)

Bài 5:
\(x^2+y^2+1\ge xy+x+y\)
\(\Leftrightarrow2\left(x^2+y^2+1\right)\ge2\left(xy+x+y\right)\)
\(\Leftrightarrow2x^2+2y^2+2\ge2xy+2x+2y\)
\(\Leftrightarrow2x^2+2y^2+2-2xy-2x-2y\ge0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(x^2-2x+1\right)+\left(y^2-2y+1\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(x-1\right)^2+\left(y-1\right)^2\ge0\left(đúng\right)\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=1\)
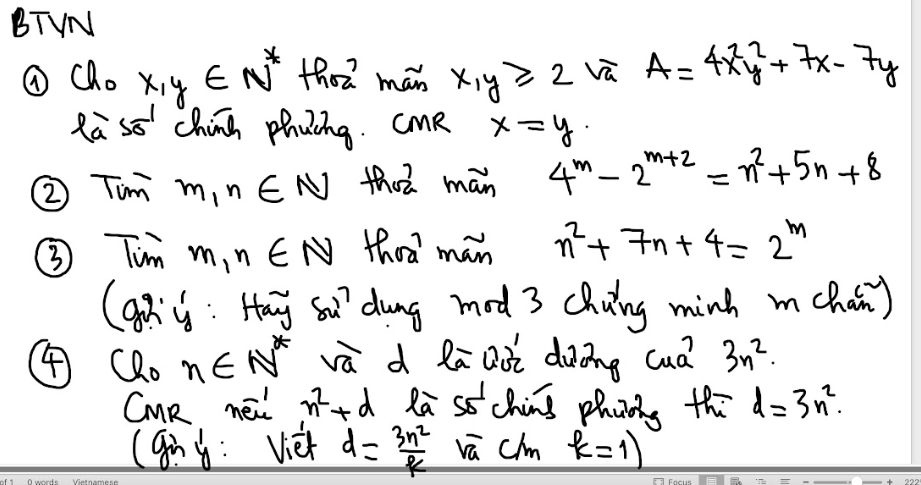





 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ

- Đây có phải là toán lớp 8 nữa không vậy :)? Mình học toán nâng cao nhưng chưa bao giờ thấy dạng này :).
b1:
do x;y thuộc số nguyên N và x,y\(\ge\)2
=>\(-4xy+1< +7x-7y< 4xy+1\)
\(\Rightarrow4x^2y^2-4xy+1< 4x^2y^2+7x-7y< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< 4x^2y^2+7x-7y< \left(2xy+1\right)^2\)
mà \(4x^2y^2+7x-7y\) là số chính phương và 1<2xy-1<2xy-1 nên ta có:
\(4x^2y^2+7x-7y-\left(2xy\right)^2\Leftrightarrow x=y\)