
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Thay x=-2 vào (1), ta được:
4+8+2m-1=0
=>2m+11=0
hay m=-11/2
b: \(\text{Δ}=\left(-4\right)^2-4\left(2m-1\right)\)
=16-8m+4
=-8m+20
Để phương trình có hai nghiệm phân biệt thì -8m+20>0
=>-8m>-20
hay m<5/2
Theo đề, ta có: \(x_1^2+x_2^2+x_1x_2=m^2-2m\)
\(\Leftrightarrow m^2-2m=\left(x_1+x_2\right)^2-x_1x_2\)
\(\Leftrightarrow m^2-2m=\left(-4\right)^2-\left(2m-1\right)\)
\(\Leftrightarrow m^2-2m=16-2m+1=17\)
hay \(m=-\sqrt{17}\)

\(1,=\left|\sqrt{7}-4\right|-2\sqrt{7}=4-\sqrt{7}-2\sqrt{7}=4-3\sqrt{7}\\ 2,\\ a,P=\dfrac{x+2\sqrt{x}+x-2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{2\sqrt{x}}\\ P=\dfrac{2x}{2\sqrt{x}}=\sqrt{x}\\ b,P>3\Leftrightarrow\sqrt{x}>3\Leftrightarrow x>9\)

4.
\(\sin\widehat{B}=\sin57^0=\dfrac{AC}{BC}\approx0,8\Leftrightarrow AC\approx0,8\cdot4,5=3,6\\ \Rightarrow AB=\sqrt{BC^2-AC^2}=2,7\left(cm\right)\left(pytago\right)\)
5.
Áp dụng HTL: \(AB^2=BH\cdot BC\Rightarrow BC=\dfrac{AB^2}{BH}=\dfrac{25}{6}\)
Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=\dfrac{10}{3}\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\Leftrightarrow\widehat{B}\approx53^0\)
Vì tg ABC vg tại A nên \(\widehat{C}=90^0-\widehat{B}=37^0\)

a) \(D=4\sqrt{\dfrac{1}{3}}+5\sqrt{12}-6\sqrt{27}\)
\(=\dfrac{4}{9}\sqrt{3}+5.2\sqrt{3}-6.3\sqrt{3}\)
\(=\dfrac{4}{9}\sqrt{3}+10\sqrt{3}-18\sqrt{3}\)
\(=-\dfrac{68}{9}\sqrt{3}\)
b) \(E=\dfrac{2}{\sqrt{3}-1}-\sqrt{4-2\sqrt{3}}\)
\(=\dfrac{2\left(\sqrt{3}+1\right)}{2}-\sqrt{\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2}\)
\(=\sqrt{3}+1-\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\sqrt{3}+1-\left(\sqrt{3}-1\right)\)
\(=\sqrt{3}+1-\sqrt{3}+1=2\)
c) \(F=\dfrac{\sqrt{15}-\sqrt{10}}{\sqrt{3}-\sqrt{2}}+\dfrac{3}{2-\sqrt{5}}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}+\dfrac{3\left(2+\sqrt{5}\right)}{-1}\)
\(=\sqrt{5}-6-3\sqrt{5}=-2\sqrt{5}-6\)


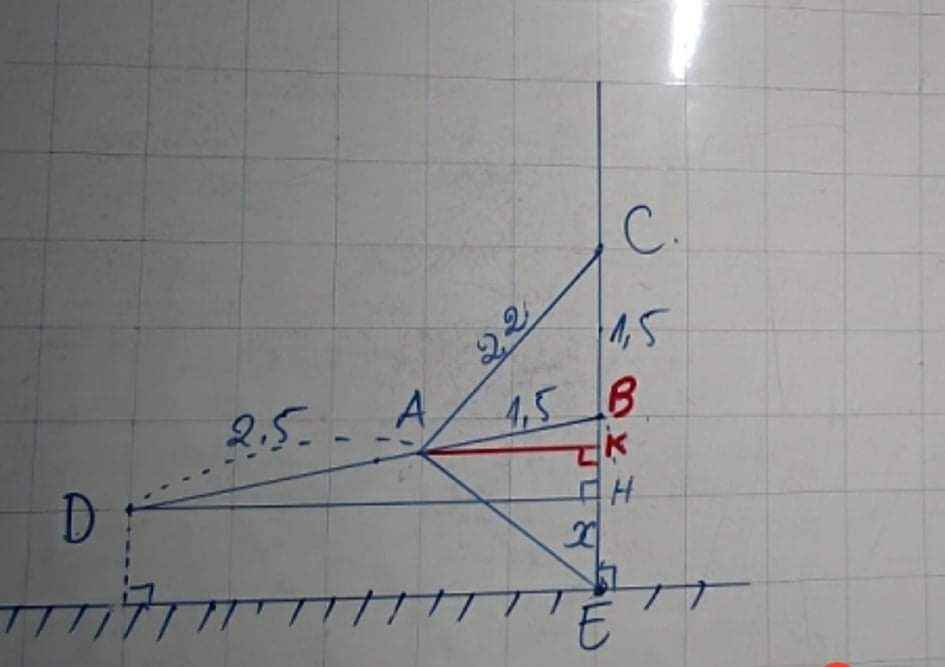
Gọi DH là khoảng cách thấp nhất từ máy bay đến mặt đất, khi đó AC có độ dài lớn nhất là 2,2m. Dựng hình chữ nhật DHEK => DH = EK
Do BA = BE = BC = 1,5m cố định nên tam giác ACE vuông tại A
Xét tam giác ACE vuông tại A có cos\(\widehat{ECA}\) = \(\dfrac{CA}{CE}=\dfrac{2,2}{3}\) => \(\widehat{ECA}\) \(\approx\) 42o50'
BA = BC => tam giác ABC cân tại B => \(\widehat{BAC}=\widehat{BCA}\) = \(\widehat{ECA}\) \(\approx\) 42o50'
=> \(\widehat{DBK}\) = \(\widehat{BAC}+\widehat{BCA}\) = 2.\(\widehat{BCA}\) = 85o40'
Xét tam giác DBK vuông tại D có: BK = BD. cos\(\widehat{DBK}\)
= 4.cos85o40' \(\approx\) 0,3022
=> DH = KE \(\approx\) 1,5 - 0,3022 \(\approx\)1,2 (m)

\(C=\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)-\sqrt{x}\left(\sqrt{x}+2\right)+6\sqrt{x}}{x-4}.\left(x-4\right)=2\sqrt{x}\)


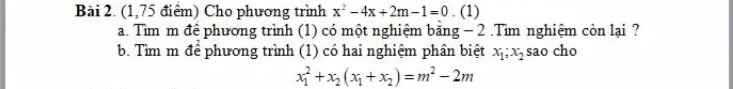



 giúp em với cần gấp ạ huhu
giúp em với cần gấp ạ huhu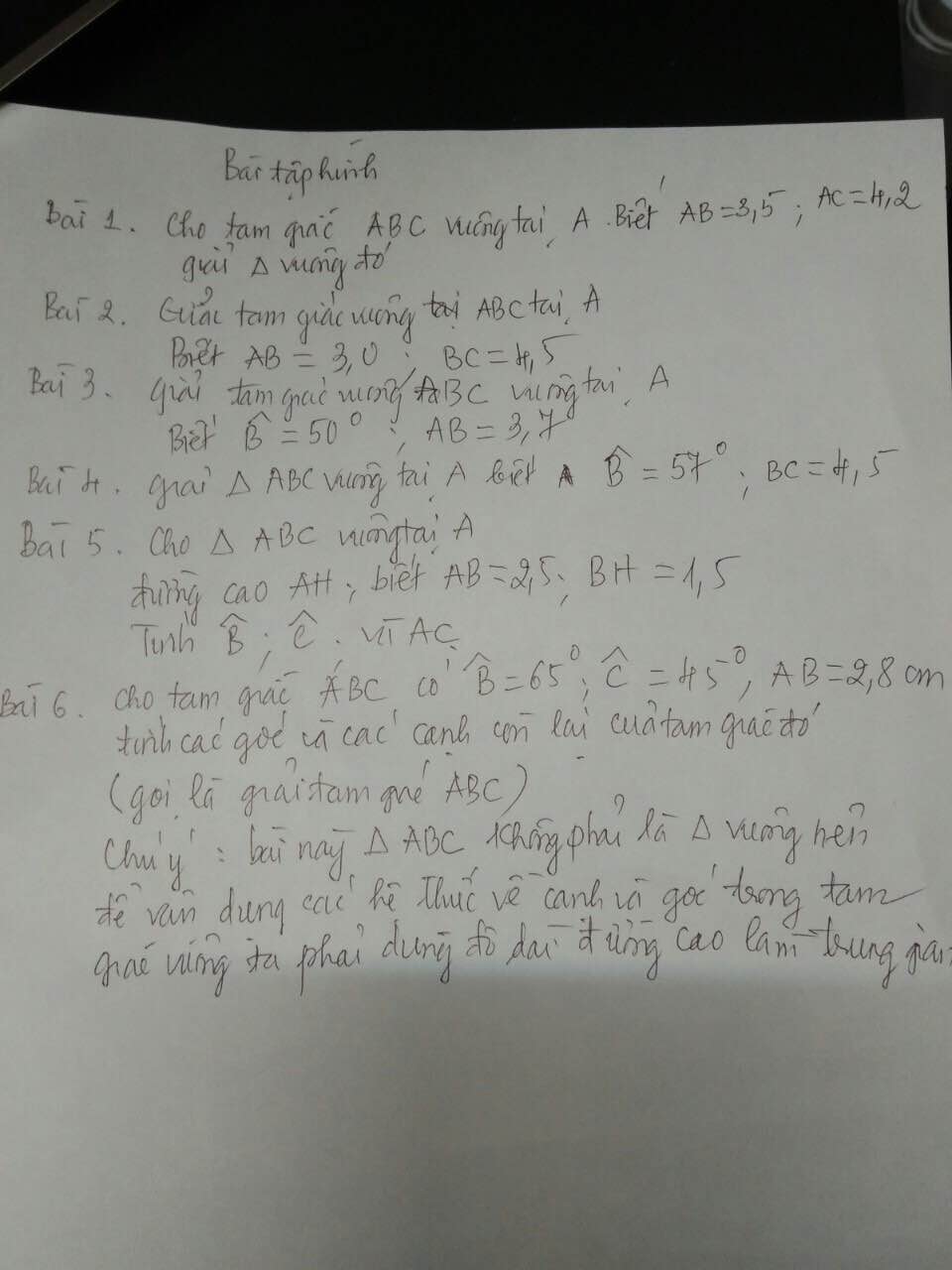

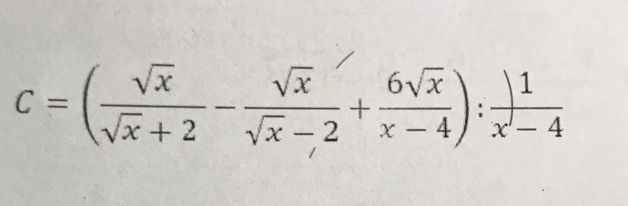

a, Vì SA ; SB lần lượt là tiếp tuyến (O) với A;B là tiếp điểm
nên ^SAO = ^SBO = 900
Xét tứ giác SAOB ta có
^SAO + ^SBO = 1800
mà 2 góc này đối
Vậy tứ giác SAOB là tứ giác nt 1 đường tròn
b, Vì H là trung điểm CD => OH vuông CD
Xét tứ giác AHOS có
^OHS = ^OAS = 900
mà 2 góc này kề, cùng nhìn cạnh OS
Vậy tứ giác AHOS là tứ giác nt 1 đường tròn
=> ^OAH = ^OSH ( góc nt chắn cung HO )
c, Xét tam giác SAC và tam giác SDA ta có
^S _ chung
^SAC = ^SDA (cùng chắn cung AC )
Vậy tam giác SAC ~ tam giác SDA (g.g)
\(\dfrac{SA}{SD}=\dfrac{SC}{SA}\Rightarrow SA^2=SC.SD\)(1)
Ta có ^SAB = ^SBA do SA = SB ( tiếp tuyến cắ nhau )
mà ^AHS = ^AOS ( góc nt chắn cung AS của tứ giác ASOH )
Mặt khác ^AOS = ^SBA ( góc nt chắn cung AS của tứ giác ASBO )
=> ^SAE = ^SHA
Xét tam giác SAE và tam giác SHA ta có
^S _ chung
^SAE = ^SHA (cmt)
Vật tam giác SAE ~ tam giác SHA (g.g)
\(\dfrac{SA}{SH}=\dfrac{SE}{SA}\Rightarrow SA^2=SE.SH\)(2)
Từ (1) ; (2) suy ra \(SE.SH=SC.SD\)