
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Ta có: 2x=3y=5z
\(\Leftrightarrow\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{\dfrac{1}{3}}=\dfrac{z}{\dfrac{1}{5}}=\dfrac{x-2y+z}{\dfrac{1}{2}-\dfrac{2}{3}+\dfrac{1}{5}}=\dfrac{14}{\dfrac{1}{30}}=420\)
Do đó: x=210; y=140; z=84

\(\frac{-3}{7}\).\(^{\left(-3\right)^2}\)-\(\sqrt{\frac{4}{49}}\)
= \(\frac{-3}{7}.9-\sqrt{\frac{4}{49}}\)
=\(\frac{-27}{7}-\sqrt{\frac{4}{49}}\)
=\(\frac{-27}{7}-\frac{2}{7}\)
=\(\frac{-29}{7}\)
Chúc bạn học tốt
\(\left|-\frac{3}{7}\right|\cdot(-3)^2-\sqrt{\frac{4}{49}}\)
\(=\frac{3}{7}\cdot9-\frac{2}{7}\)
\(=\frac{27}{7}-\frac{2}{7}=\frac{25}{7}\)


b: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
\(=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}\)
\(=k^2\)(1)
Ta có: \(\dfrac{a^2-c^2}{b^2-d^2}\)
\(=\dfrac{\left(bk\right)^2-\left(dk\right)^2}{b^2-d^2}\)
\(=k^2\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{a^2-c^2}{b^2-d^2}\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4bk+3dk}{4b+3d}=k\)
\(\dfrac{4a-3c}{4b-3d}=\dfrac{4bk-3dk}{4b-3d}=k\)
Do đó: \(\dfrac{4a+3c}{4b+3d}=\dfrac{4a-3c}{4b-3d}\)

a) \(\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow\left|x\right|=\dfrac{7}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
b) \(\left|x-1,2\right|=2,8\)
\(\Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=4\\x=-1,6\end{matrix}\right.\)
\(a,\left|x\right|=3\dfrac{1}{2}\)
\(\Rightarrow x=\left[{}\begin{matrix}3\dfrac{1}{2}\\-3\dfrac{1}{2}\end{matrix}\right.\)
\(b,\left|x-1,2\right|=2,8\\ \Rightarrow\left[{}\begin{matrix}x-1,2=2,8\\x-1,2=-2,8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2,8+1,2=4\\x=-2,8+1,2=-1,6\end{matrix}\right.\)
Vậy \(x\in\left\{4;-1,6\right\}\)

Lời giải:
a.
$A=(-2x^3+6x^3)+(6x^3y-25x^3y)+(7y+8y)-20$
$=4x^3-19x^3y+15y-20$
b.
$B=(5x^3-14x^3)+(9xy^4-13xy^4)-3y^2+(17-23)$
$=-9x^3-4xy^4-3y^2-6$
b.
Bậc của $A$ gắn với $-19x^3y$, là $3+1=4$
Bậc của $B$ gắn với $-4xy^4$, là $1+4=5$
ab, \(A=-2x^3-19x^3y+15y-20\)
-> bậc 4
\(B=-9x^3-4xy^4-3y^2-5\)
-> bậc 5



a) Xét \(\Delta ADK\)và \(\Delta BDE\)có:
AD = BD (gt)
\(\widehat{ADK}=\widehat{BDE}\)
DK = DE (gt)
Suy ra \(\Delta ADK\)\(=\Delta BDE\left(c-g-c\right)\)
\(\Rightarrow\widehat{DAK}=\widehat{DBE}\)(hai góc tương ứng) và AK = BE
Mà 2 góc này ở vị trí so le trong nên \(AK//BC\)(đpcm)
b) Xét \(\Delta EIC\)và \(\Delta AIK\)có:
EI = AI (gt)
\(\widehat{IEC}=\widehat{IAK}\)(\(AK//BC\),so le trong)
EC = AK ( Vì AK = BE mà BE = EC)
Suy ra \(\Delta EIC\)\(=\Delta AIK\left(c-g-c\right)\)
\(\Rightarrow KI=CI\)(hai cạnh tương ứng)
Từ đề bài suy ra DE là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DE//AC\)
CM tương tự được: \(\Delta KIE=\Delta CIA\)
Sao đó c/m \(KIC=180^0\)rồi suy ra I là trung điểm của KC



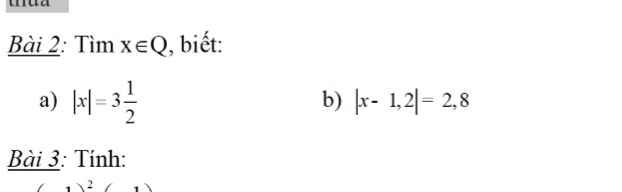
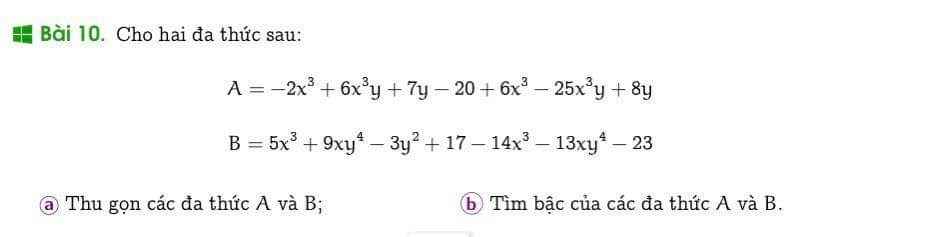 Giúp mik vớii ( chi tiết nếu đc ạ)
Giúp mik vớii ( chi tiết nếu đc ạ) 

`@` `\text {Ans}`
`\downarrow`
\(-7\in\text{N}\)
\(-7\in\text{Z}\)
\(-7\in\text{Q}\)
\(-\dfrac{5}{7}\notin\text{Z}\)
\(-\dfrac{5}{7}\in\text{Q}\)