
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: \(\sqrt{\dfrac{1}{200}}=\dfrac{\sqrt{2}}{20}\)
2: \(\dfrac{5}{1-\sqrt{6}}=-1-\sqrt{6}\)
3: \(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{1+\sqrt{2}}\)
\(=\dfrac{1+\sqrt{2}-1+\sqrt{2}}{-1}\)
\(=-2\sqrt{2}\)

2: Ta có: \(\sqrt{16-6\sqrt{7}}\cdot\left(3+\sqrt{7}\right)\)
\(=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)\)
=9-7
=2
3: Ta có: \(\left(\sqrt{6}+\sqrt{14}\right)\cdot\sqrt{5-2\sqrt{21}}\)
\(=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)\)
=7-3
=4
\(1,=\sqrt{\left(5+2\sqrt{6}\right)^2}-\sqrt{\left(3-\sqrt{6}\right)^2}=5+2\sqrt{6}-3+\sqrt{6}=2+3\sqrt{6}\\ 2,=\sqrt{\left(3-\sqrt{7}\right)^2}\left(3+\sqrt{7}\right)=\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)=9-7=2\\ 3,=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{10-2\sqrt{21}}=\left(\sqrt{3}+\sqrt{7}\right)\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}\\ =\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)=7-3=4\\ 4,=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{6+2\sqrt{5}}+\sqrt{4-2\sqrt{3}}\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+1+\sqrt{3}-1\right)\\ =\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)=5-3=2\)
\(5,\\ =\sqrt{\left(3\sqrt{3}-5\right)^2}+\sqrt{\left(5-2\sqrt{3}\right)^2}=3\sqrt{3}-5+5-2\sqrt{3}=\sqrt{3}\\ 6,=\sqrt{13-4\sqrt{10}}-\sqrt{53+12\sqrt{10}}\\ =\sqrt{\left(2\sqrt{2}-\sqrt{5}\right)^2}-\sqrt{\left(3\sqrt{5}-2\sqrt{2}\right)^2}\\ =2\sqrt{2}-\sqrt{5}-3\sqrt{5}+2\sqrt{2}=4\sqrt{2}-4\sqrt{5}\)



ta có
\(A=B.\left|x-4\right|\Leftrightarrow\frac{\sqrt{x}+2}{\sqrt{x}-5}=\frac{1}{\sqrt{x}-5}.\left|x-4\right|\Leftrightarrow\sqrt{x}+2=\left|x-4\right|\)
Vậy :
\(\orbr{\begin{cases}\sqrt{x}+2=x-4\\\sqrt{x}+2=-x+4\end{cases}}\Leftrightarrow\orbr{\begin{cases}x-\sqrt{x}-6=0\\x+\sqrt{x}-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}\sqrt{x}=3\\\sqrt{x}=1\end{cases}}}\)\(\Leftrightarrow\orbr{\begin{cases}x=9\\x=1\end{cases}}\)


Câu II:
a: \(P=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{4\sqrt{x}}{x-1}\right):\left(\dfrac{x+\sqrt{x}+5}{x-1}-\dfrac{1}{\sqrt{x}-1}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x+\sqrt{x}+5}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right)\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2+4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+5-\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1+4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+4}\)
\(=\dfrac{8\sqrt{x}}{x+4}\)
Câu IV
3: xy-x-y=2
=>xy-x-y+1=3
=>x(y-1)-(y-1)=3
=>(x-1)(y-1)=3
=>\(\left(x-1\right)\cdot\left(y-1\right)=1\cdot3=3\cdot1=\left(-1\right)\cdot\left(-3\right)=\left(-3\right)\cdot\left(-1\right)\)
=>\(\left(x-1;y-1\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(2;4\right);\left(4;2\right);\left(0;-2\right);\left(-2;0\right)\right\}\)
2:
Khoảng cách từ O(0;0) đến (d) là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot\left(m-4\right)+0\cdot\left(m-3\right)-1\right|}{\sqrt{\left(m-4\right)^2+\left(m-3\right)^2}}\)
\(=\dfrac{1}{\sqrt{2m^2-14m+25}}\)
Để d(O;(d)) lớn nhất thì \(2m^2-14m+25\) nhỏ nhất
\(2m^2-14m+25\)=\(2\left(m^2-7m+12,5\right)\)
\(=2\left(m^2-2\cdot m\cdot\dfrac{7}{2}+\dfrac{49}{4}+\dfrac{1}{4}\right)\)
\(=2\left(m-\dfrac{7}{2}\right)^2+\dfrac{1}{2}>=\dfrac{1}{2}\)
Dấu '=' xảy ra khi m=7/2
Vậy: m=7/2


19
Từ pt đầu ta có:
\(x^2-xy-2xy+2y^2=0\)
\(\Leftrightarrow x\left(x-y\right)-2y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-2y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=y\\x=2y\end{matrix}\right.\)
TH1: \(x=y\) thế xuống pt dưới:
\(y^2-y-y^2=1\Rightarrow y=-1\Rightarrow x=-1\)
TH2: \(x=2y\) thế xuống pt dưới:
\(\left(2y\right)^2-2y-y^2=1\Leftrightarrow3y^2-2y-1=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-\dfrac{1}{3}\Rightarrow x=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ là: \(\left(x;y\right)=\left(-1;-1\right);\left(1;2\right);\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)\)
21.
Từ pt đầu:
\(xy+2=2x+y\Leftrightarrow xy-y+2-2x=0\)
\(\Leftrightarrow y\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(y-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
TH1: \(x=1\) thế xuống pt dưới:
\(2y+y^2+3y=6\Leftrightarrow y^2+5y-6=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\\y=-6\end{matrix}\right.\)
TH2: \(y=2\) thế xuông pt dưới
\(4x+4+6=6\Rightarrow x=-1\)
Vậy nghiệm của pt là: \(\left(x;y\right)=\left(1;1\right);\left(1;-6\right);\left(-1;2\right)\)


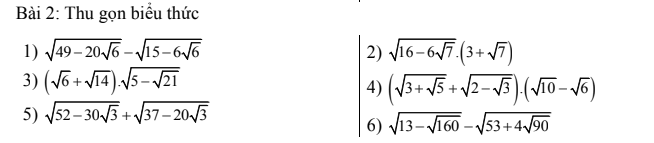







1) \(\sqrt{\dfrac{1}{200}}\) 2) \(\dfrac{5}{1-\sqrt{6}}\)
\(=\sqrt{\dfrac{1^2}{10^2.2}}\) \(=\dfrac{1-\sqrt{6}+4+\sqrt{6}}{1-\sqrt{6}}\)
\(=\dfrac{1}{10\sqrt{2}}\) \(=1+\dfrac{4+\sqrt{6}}{1-\sqrt{6}}\)
Bài 2:
1. \(\sqrt{2x-5}=7\) ĐKXĐ: \(x\ge\dfrac{5}{2}\)
<=> 2x - 5 = 72
<=> 2x - 5 = 49
<=> 2x = 54
<=> x = 27 (TM)
2. \(3+\sqrt{x-2}=4\) ĐKXĐ: \(x\ge2\)
<=> \(\sqrt{x-2}=1\)
<=> x - 2 = 1
<=> x = 3 (TM)
3. \(\sqrt{x^2-2x+1}=1\)
<=> \(\sqrt{\left(x-1\right)^2}=1\)
<=> \(|x-1|=1\)
<=> \(\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4. \(\sqrt{x^2-4x+4}=1\)
<=> \(\sqrt{\left(x-2\right)^2}=1\)
<=> \(|x-2|=1\)
<=> \(\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5. \(\sqrt{4x^2+1-4x}=\sqrt{x^2+16+8x}\)
<=> \(\left(\sqrt{4x^2+1-4x}\right)^2=\left(\sqrt{x^2+16+8x}\right)^2\)
<=> \(|4x^2+1-4x|=|x^2+16+8x|\)
<=> \(\left[{}\begin{matrix}4x^2+1-4x=x^2+16+8x\\4x^2+1-4x=-\left(x^2+16+8x\right)\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}4x^2-x^2-4x-8x+1-16=0\\4x^2+1-4x=-x^2-16-8x\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}3x^2-12x-15=0\\5x^2+4x+17=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}3x^2+3x-15x-15=0\\VNghiệm\end{matrix}\right.\)
<=> 3x(x + 1) - 15(x + 1) = 0
<=> (3x - 15)(x + 1) = 0
<=> \(\left[{}\begin{matrix}3x-15=0\\x+1=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)