
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


VD5:
\(A\cap B\ne\varnothing\Leftrightarrow2m-1\le m+3\)
\(\Leftrightarrow m\le4\)
VD6:
\(A\cap B\ne\varnothing\Leftrightarrow9a>\dfrac{4}{a}\)
\(\Leftrightarrow\dfrac{9a^2-4}{a}>0\)
\(\Leftrightarrow9a^2-4< 0\) (do \(a< 0\))
\(\Rightarrow-\dfrac{2}{3}< a< \dfrac{2}{3}\)
\(\Rightarrow-\dfrac{2}{3}< a< 0\)
VD6:
\(A\cap B=A\Leftrightarrow A\subset B\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\ge m\\3\le m+5\end{matrix}\right.\) \(\Rightarrow-2\le m\le-1\)



1.
\(\dfrac{1-cosx+cos2x}{sin2x-sinx}=\dfrac{1-cosx+2cos^2x-1}{2sinx.cosx-sinx}\)
\(=\dfrac{cosx\left(2cosx-1\right)}{sinx\left(2cosx-1\right)}=\dfrac{cosx}{sinx}=cotx\)
2.
\(\dfrac{1+tan^4x}{tan^2x+cot^2x}=\dfrac{1+tan^4x}{tan^2x+\dfrac{1}{tan^2x}}=\dfrac{1+tan^4x}{\dfrac{tan^4x+1}{tan^2x}}=tan^2x\)
3.
\(sin^4x+cos^4x=sin^4x+cos^4x+2sin^2x.cos^2x-2sin^2x.cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x\)
\(=1-2sin^2x.cos^2x\)
4.
Áp dụng câu 3:
\(sin^4x+cos^4x=1-2sin^2x.cos^2x\)
\(=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2\)
\(=1-\dfrac{1}{2}sin^22x\)
5.
\(sin\left(x+y\right)sin\left(x-y\right)=\dfrac{1}{2}cos\left[\left(x-y\right)-\left(x+y\right)\right]-\dfrac{1}{2}cos\left[\left(x-y\right)+\left(x+y\right)\right]\)
\(=\dfrac{1}{2}\left(cos2y-cos2x\right)=\dfrac{1}{2}\left(1-2sin^2y\right)-\dfrac{1}{2}\left(1-2sin^2x\right)\)
\(=sin^2x-sin^2y\)
6.
\(tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}\)
\(=\dfrac{1}{sinx.cosx}=\dfrac{2}{2sinx.cosx}=\dfrac{2}{sin2x}\)



a: A={\(x\in N\)|\(\left\{{}\begin{matrix}x< 20\\x⋮5\end{matrix}\right.\)}
b: B={\(x\in N\)|\(\left\{{}\begin{matrix}x=4k+1\\k\in N\end{matrix}\right.\)}

a.
Áp dụng định lý hàm cos:
\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosA}=\sqrt{19}\)
Áp dụng công thức trung tuyến:
\(AM=\sqrt{\dfrac{2\left(AB^2+AC^2\right)-BC^2}{4}}=\dfrac{\sqrt{7}}{2}\)
b.
\(2\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\Leftrightarrow2\overrightarrow{IB}+2\overrightarrow{BA}+\overrightarrow{IB}=\overrightarrow{0}\Leftrightarrow\overrightarrow{IB}=\dfrac{2}{3}\overrightarrow{AB}\Rightarrow\overrightarrow{BI}=-\dfrac{2}{3}\overrightarrow{AB}\)
\(\overrightarrow{JB}-2\overrightarrow{JC}=\overrightarrow{0}\Rightarrow\overrightarrow{JB}=2\overrightarrow{JC}=2\overrightarrow{JB}+2\overrightarrow{BC}\Rightarrow\overrightarrow{JB}=-2\overrightarrow{BC}\Rightarrow\overrightarrow{BJ}=2\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BI}.\overrightarrow{BJ}=-\dfrac{2}{3}\overrightarrow{AB}.2\overrightarrow{BC}=-\dfrac{4}{3}\overrightarrow{AB}.\overrightarrow{BC}=-\dfrac{4}{3}\overrightarrow{AB}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{4}{3}AB^2-\dfrac{4}{3}\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{4}{3}.2^2-\dfrac{4}{3}.2.3.cosA=\dfrac{28}{3}\)
Độ dài IJ:
Ta có: \(\overrightarrow{BI}=-\dfrac{2}{3}\overrightarrow{AB}\Rightarrow BI=\dfrac{2}{3}AB=\dfrac{4}{3}\)
\(\overrightarrow{BJ}=2\overrightarrow{BC}\Rightarrow BJ=2BC=2\sqrt{19}\)
Từ đó:
\(IJ^2=\overrightarrow{IJ}^2=\left(\overrightarrow{IB}+\overrightarrow{BJ}\right)^2=IB^2+BJ^2+2\overrightarrow{IB}.\overrightarrow{BJ}\)
\(=IB^2+BJ^2-2\overrightarrow{BI}.\overrightarrow{BJ}\)
\(=\left(\dfrac{4}{3}\right)^2+\left(2\sqrt{19}\right)^2-2.\dfrac{28}{3}=...\)

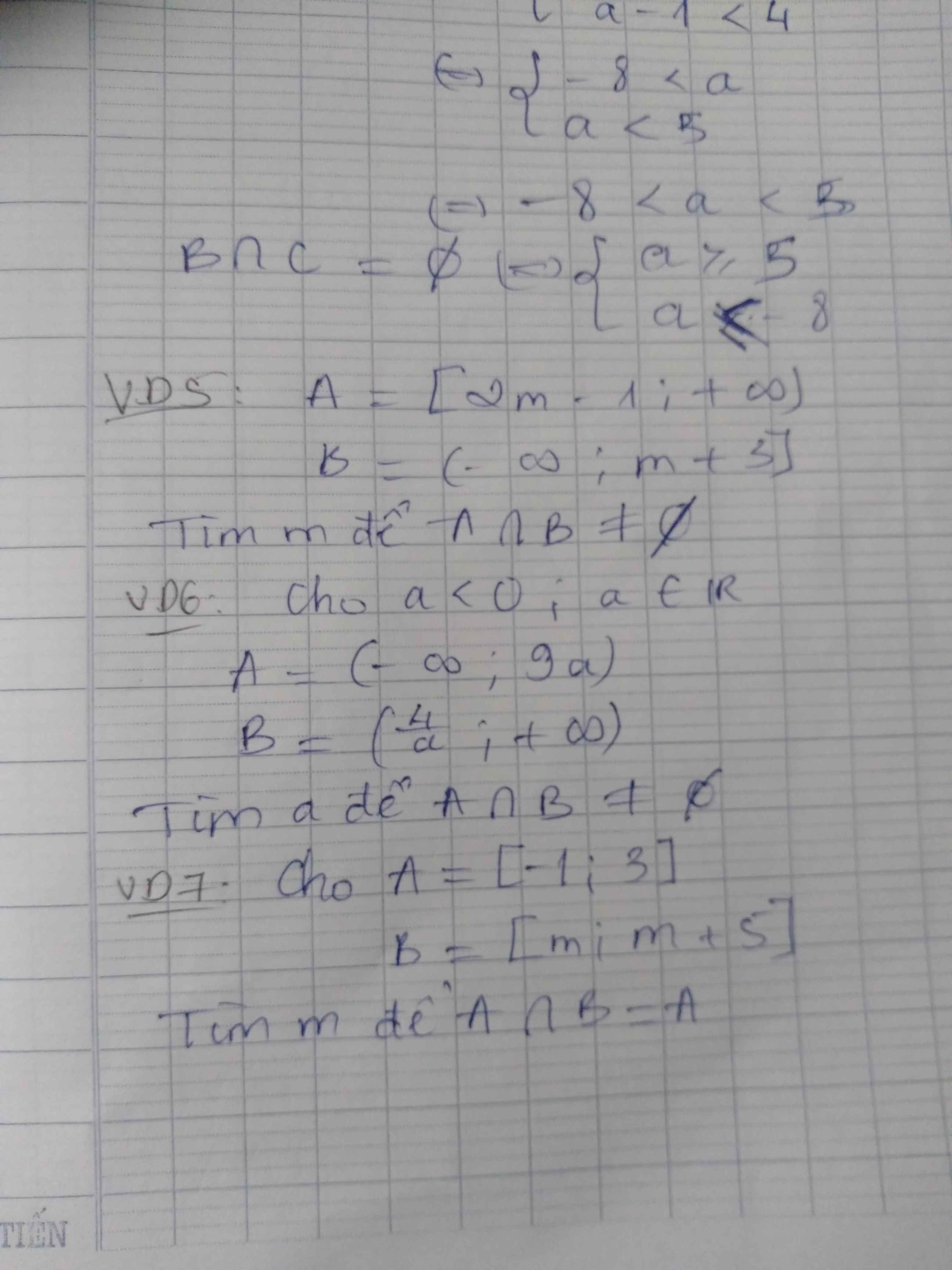

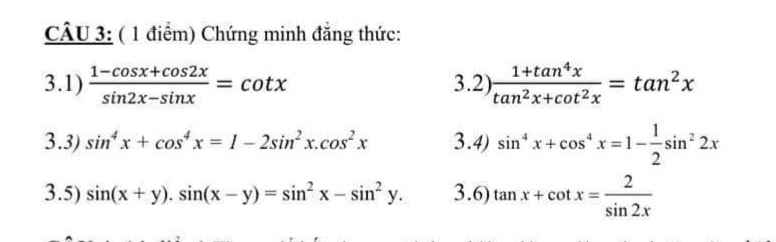



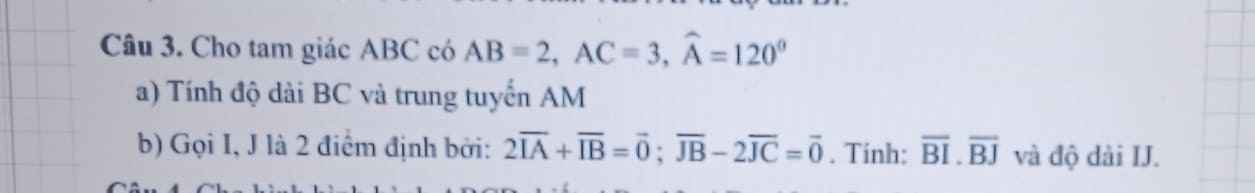
a/ △= b^2-4ac
= 4(m+2)^2-4(2m^2+7)= -4m^2+16m-12
Để phương trình có nghiệm kép thì △=0
hay -4m^+16m-12=0
<=> m=3 và m=1
b/
△=b^2-4ac=4(3m-2)^2-4(m+2)(m+2)
=32m^2-44m
Để phương trình có nghiệm kép thì △=0
hay 32m^-44m=0
<=>m=11/8 và m=0