
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: ΔABC đều
mà BP,CM là các đường trung tuyến
nên BP,CM là các đường cao
Xét tứ giác BMPC có
\(\widehat{BMC}=\widehat{BPC}=90^0\)
nên BMPC là tứ giác nội tiếp
hay B,M,P,C cùng thuộc 1 đường tròn



ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm



b: \(\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right):\dfrac{a-1}{\sqrt{a}+1}\)
\(=\left(a-2\sqrt{a}+1\right)\cdot\dfrac{\left(\sqrt{a}+1\right)}{a-1}\)
\(=\sqrt{a}-1\)

\(P=\dfrac{4}{3}.\dfrac{\sqrt{x}}{x-\sqrt{x}+1}=\dfrac{4}{3}\left(1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+1}\right)=\dfrac{4}{3}-\dfrac{4}{3}.\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+1}\le\dfrac{4}{3}\)
\(P_{max}=\dfrac{4}{3}\) khi \(x=1\)
Do \(\left\{{}\begin{matrix}\sqrt{x}\ge0\\x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow P\ge0\)
\(P_{min}=0\) khi \(x=0\)
a: Ta có: \(P=\left(\dfrac{x+2}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right)\cdot\dfrac{4\sqrt{x}}{3}\)
\(=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\)
\(=\dfrac{4\sqrt{x}}{3x-3\sqrt{x}+3}\)

Ta có: \(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-2\cdot\left(\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{xz}\right)}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-2\cdot\dfrac{x+y+z}{xyz}}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\)







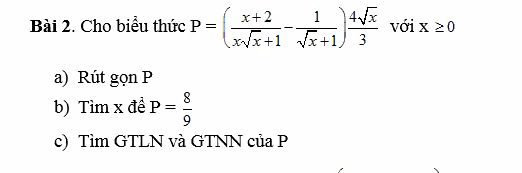

a: Thay x=2 vào y=2x-1, ta được:
y=4-1=3
Thay x=2 và y=3 vào y=ax-4, ta được:
2a-4=3
hay \(a=\dfrac{7}{2}\)