
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1 : a . \(lim\dfrac{9n^2-3n-1}{7n^3+3n^2}=lim\dfrac{\dfrac{9}{n}-\dfrac{3}{n^2}-\dfrac{1}{n^3}}{7+\dfrac{3}{n}}=0\)
b. \(lim_{x\rightarrow2}\dfrac{\sqrt{4x+1}-3}{4-x^2}=lim_{x\rightarrow2}\dfrac{4x+1-9}{\left(\sqrt{4x+1}+3\right)\left(4-x^2\right)}\)
\(=lim_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(\sqrt{4x+1}+3\right)\left(2-x\right)\left(2+x\right)}\)
\(=lim_{x\rightarrow2}\dfrac{-4}{\left(\sqrt{4x+1}+3\right)\left(2+x\right)}=\dfrac{-4}{\left(3+3\right)\left(2+2\right)}=-\dfrac{1}{6}\)
Câu 2 : Ta có : f(x) = \(\left\{{}\begin{matrix}2x^2+x\left(x< 2\right)\\mx-1\left(x\ge2\right)\end{matrix}\right.\)
TXĐ : D = R . Với x < 2 ; hàm số liên tục
Với x > 2 ; hàm số liên tục
Với x = 2 , ta có : \(lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^-}2x^2+x=2.2^2+2=10\)
\(lim_{x\rightarrow2^+}f\left(x\right)=lim_{x\rightarrow2^+}mx-1=2m-1\)
Hàm số liên tục trên R <=> Hàm số liên tục tại x = 2
\(\Leftrightarrow lim_{x\rightarrow2^-}f\left(x\right)=lim_{x\rightarrow2^+}f\left(x\right)\)
\(\Leftrightarrow10=2m-1\) \(\Leftrightarrow m=\dfrac{11}{2}\)
Vậy ...

Ớ :D? Này hình như là đề thi chọn HSG Quốc gia môn Toán đúng ko nhờ :D? Thằng bạn kêu tui làm thử mà nhìn đề xong tui shock nặng luôn :b Lót dép hóng ai đó làm :3
Ò đúng rồi, đề thi HSG đó, con bạn mình nó kêu đi hỏi hộ nó để nó so keys, cơ mà thôi chắc không cần nữa rồi :v

8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)

a.
\(SH\perp\left(ABC\right)\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)
\(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\Rightarrow\Delta SBH\) vuông tại H
\(BH=\dfrac{1}{2}BC=a\Rightarrow SH=\sqrt{SB^2-BH^2}=a\sqrt{3}\)
\(SH\perp\left(ABC\right)\Rightarrow HA\) là hình chiếu vuông góc của SA lên (ABC)
\(\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(AH=\dfrac{1}{2}BC=a\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow tan\widehat{SAH}=\dfrac{SH}{AH}=\sqrt{3}\Rightarrow\widehat{SAH}=60^0\)
b.
H là trung điểm BC, M là trung điểm AB \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH||AC\Rightarrow MH\perp AB\) (do \(AB\perp AC\))
Lại có \(SH\perp\left(ABC\right)\Rightarrow SH\perp AB\)
\(\Rightarrow AB\perp\left(SMH\right)\)
Mà \(AB=\left(SAB\right)\cap\left(ABC\right)\Rightarrow\widehat{SMH}\) là góc giữa (SAB) và (ABC)
\(AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\) \(\Rightarrow MH=\dfrac{1}{2}AC=\dfrac{a\sqrt{3}}{2}\) (đường trung bình)
\(\Rightarrow tan\widehat{SMH}=\dfrac{SH}{MH}=2\Rightarrow\widehat{SMH}\approx63^023'\)
c.
Theo cmt: \(\left\{{}\begin{matrix}MH\perp SH\\MH\perp AB\end{matrix}\right.\) \(\Rightarrow MH\) là đường vuông góc chung của SH và AB
\(\Rightarrow d\left(SH;AB\right)=MH=\dfrac{a\sqrt{3}}{2}\)
Từ H kẻ HK vuông góc SM (K thuộc SM)
\(AB\perp\left(SMH\right)\Rightarrow AB\perp HK\)
\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
Hệ thức lượng trong tam giác vuông SMH:
\(HK=\dfrac{SH.MH}{\sqrt{SH^2+MH^2}}=\dfrac{a\sqrt{15}}{5}\)





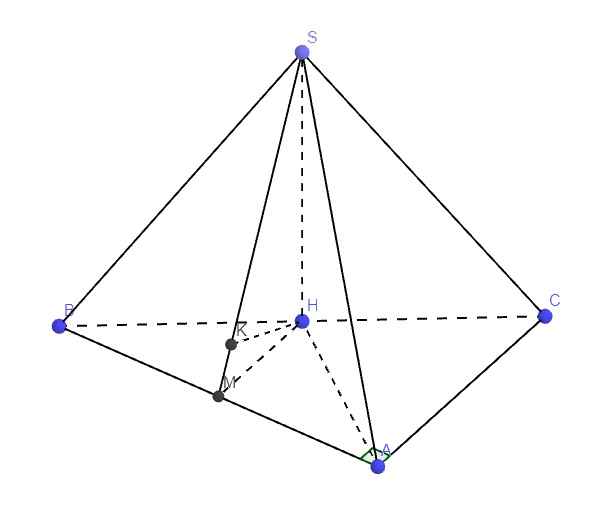
Do ABCD.A'B'C'D' là hình hộp chữ nhật \(\Rightarrow CD\perp\left(ADD'A'\right)\Rightarrow CD\perp AD'\)
Lại có ADD'A' là hình vuông \(\Rightarrow AD'\perp A'D\)
\(\Rightarrow AD'\perp\left(A'B'CD\right)\)
Mà \(AD'\in\left(ABC'D'\right)\Rightarrow\left(ABC'D'\right)\perp\left(A'B'CD\right)\)
b.
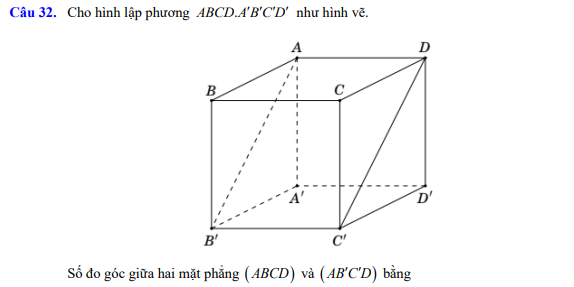
\(AA'\perp\left(ABCD\right)\) (t/c lập phương) \(\Rightarrow AA'\perp BD\)
Lại có \(BD\perp AC\) (ABCD là hình vuông)
\(\Rightarrow BD\perp\left(ACC'A'\right)\)
Mà \(BD\in\left(A'BD\right)\Rightarrow\left(ACC'A'\right)\perp\left(A'BD\right)\)
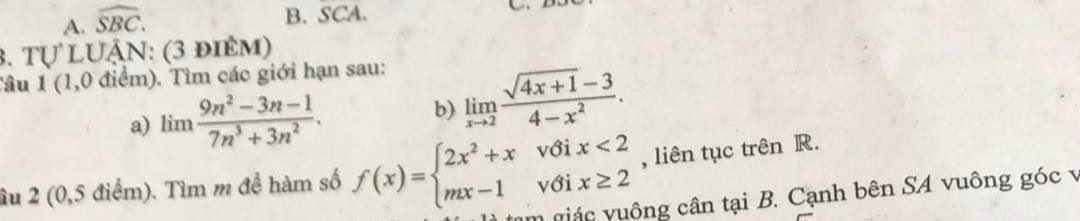







2.
\(cosx+cos3x=1+\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow2cos2x.cosx=1+cos2x+sin2x\)
\(\Leftrightarrow2cos2x.cosx=2cos^2x+2sinx.cosx\)
\(\Leftrightarrow cosx\left(cos2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cos^2x-sin^2x-cosx-sinx\right)=0\)
\(\Leftrightarrow cosx\left(cosx+sinx\right)\left(cosx-sinx-1\right)=0\)
\(\Leftrightarrow cosx.\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right).\left[\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sin\left(x+\dfrac{\pi}{4}\right)=0\\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x+\dfrac{\pi}{4}=\pm\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=-\dfrac{\pi}{4}+k\pi\\x=k2\pi\end{matrix}\right.\)
Mình cảm ơn