
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 2:
a) Xét tứ giác KPIQ có
\(\widehat{KPI}\) và \(\widehat{KQI}\) là hai góc đối
\(\widehat{KPI}+\widehat{KQI}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: KPIQ là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Câu 1:
\(a,B=\dfrac{2\cdot3-1}{9-4}=\dfrac{5}{5}=1\\ b,A=\dfrac{x-2\sqrt{x}+x+2\sqrt{x}-2x+\sqrt{x}+5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ b,\dfrac{A}{B}=\dfrac{\sqrt{x}+5}{x-4}\cdot\dfrac{x-4}{2\sqrt{x}-1}=\dfrac{\sqrt{x}+5}{2\sqrt{x}-1}< 0\\ \Leftrightarrow2\sqrt{x}-1< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow\sqrt{x}< \dfrac{1}{2}\Leftrightarrow0\le x< \dfrac{1}{4}\)
1 a) Với \(a\ge0\) và \(a\ne4\) ta có
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+2}-\dfrac{\sqrt{x}}{2-\sqrt{x}}-\dfrac{2x-2\sqrt{x}-5}{x-4},B=\dfrac{2\sqrt{x}-1}{x-4}\)
a)
A=\(\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}-\dfrac{\sqrt{x}}{-\left(\sqrt{x}-2\right)}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)
A=\(\dfrac{\sqrt{x}+\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)
A=\(\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)+\sqrt{x}\left(\sqrt{x}+2\right)}{x-4}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)
A=\(\dfrac{x-2\sqrt{x}+x+2\sqrt{x}}{x-4}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)=\(\dfrac{2x}{x-4}-\dfrac{2x-2\sqrt{x}-5}{x-4}\)=\(\dfrac{2x-2x+2\sqrt{x}+5}{x-4}\)
A=\(\dfrac{2\sqrt{x}+5}{x-4}\)
Gía Trị Của B Khi x=9 Là ;
B=\(\dfrac{2\sqrt{9}-1}{9-4}=\dfrac{6-1}{5}=\dfrac{5}{5}=1\)
:)) câu c ko chắc :V
để \(\dfrac{A}{B}< 0\)(=)\(\dfrac{2\sqrt{x}+5}{x-4}:\dfrac{2\sqrt{x}-1}{x-4}\left(=\right)\dfrac{2\sqrt{x}+4}{x-4}\cdot\dfrac{x-4}{2\sqrt[]{x}-1}\left(=\right)\dfrac{\left(2\sqrt{x}+4\right)\left(x-4\right)}{\left(x-4\right)\left(2\sqrt{x}-1\right)}\)(=)\(\dfrac{2\sqrt{x}+4}{2\sqrt{x}-1}\)<0(=) bí :V

Bài 3:
Ta có: ΔMNK vuông tại M
nên \(\widehat{N}+\widehat{K}=90^0\)
hay \(\widehat{K}=30^0\)
Xét ΔMNK vuông tại M có
\(NK=\dfrac{MN}{\dfrac{1}{2}}=\dfrac{10}{\dfrac{1}{2}}=20\left(cm\right)\)
Áp dụng định lí Pytago vào ΔMNK vuông tại M, ta được:
\(NK^2=MK^2+MN^2\)
\(\Leftrightarrow MK^2=300\)
hay \(MK=10\sqrt{3}\left(cm\right)\)

1.
Do $a>1$ nên $a-1>0; 2a+1>0$. Khi đó
$A=\sqrt{(a-1)^2(2a+1)^2}=\sqrt{(a-1)^2}.\sqrt{(2a+1)^2}$
$=|a-1|.|2a+1|=(a-1)(2a+1)$
2.
$B=\sqrt{(b-1)(b+7)+16}=\sqrt{b^2+6b-7+16}=\sqrt{b^2+6b+9}$
$=\sqrt{(b+3)^2}=|b+3|=-(b+3)$ do $b+3<0$ với mọi $b< -3$

1.
\(P=\dfrac{3}{\sqrt{x}+3}\le\dfrac{3}{0+3}=1\)
\(\Rightarrow maxP=1\Leftrightarrow x=0\)
2.
\(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}=\dfrac{2\left(\sqrt{x}+1\right)-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\ge2-\dfrac{3}{0+1}=-1\)
\(\Rightarrow minA=-1\Leftrightarrow x=0\)

a.\(5x^2-4x-1=0\)
\(\Delta=\left(-4\right)^2-4.5.\left(-1\right)=16+20=36>0\)
=> pt có 2 nghiệm phân biệt
\(\left\{{}\begin{matrix}x_1=\dfrac{4+\sqrt{36}}{10}=1\\x_2=\dfrac{4-\sqrt{36}}{10}=-\dfrac{1}{5}\end{matrix}\right.\)
b.\(7x^2-2\sqrt{7}x+1=0\)
\(\Delta=\left(-2\sqrt{7}\right)^2-4.1.7\)
\(=28-28=0\)
=> pt có nghiệm kép
\(x_1=x_2=\dfrac{2\sqrt{7}}{2.7}=\dfrac{\sqrt{7}}{7}\)
a, \(\Delta=\left(-4\right)^2-4.5.\left(-1\right)=16+20=36>0\)
\(x_1=\dfrac{4+6}{10}=1\\ x_2=\dfrac{4-6}{10}=\dfrac{-1}{5}\)
\(b,\Delta=\left(-2\sqrt{7}\right)^2-4.7.1=28-28=0\)
\(\Rightarrow\) pt có nghiệm kép là: \(\dfrac{2\sqrt{7}}{14}=\dfrac{\sqrt{7}}{7}\)
\(c,4x^2-2=0\\ \Leftrightarrow2x^2-1=0\\ \Leftrightarrow x^2=\dfrac{1}{2}\\ \Leftrightarrow x=\pm\dfrac{\sqrt{2}}{2}\)
\(d,\left\{{}\begin{matrix}4x+y=3\\2x-3y=8\end{matrix}\right.\\ \Leftrightarrow \left\{{}\begin{matrix}y=3-4x\\2x-3\left(3-4x\right)=8\end{matrix}\right.\\\Leftrightarrow\left\{{}\begin{matrix}y=3-4x\\2x-9+12x=8\end{matrix}\right.\Leftrightarrow\\ \left\{{}\begin{matrix}y=3-4x\\14x=17\end{matrix}\right.\Leftrightarrow\\ \left\{{}\begin{matrix}y=3-4.\dfrac{17}{14}\\x=\dfrac{17}{14}\end{matrix}\right.\Leftrightarrow\\ \left\{{}\begin{matrix}y=-\dfrac{13}{7}\\x=\dfrac{17}{14}\end{matrix}\right.\)

Bài 2:
a: =>2x+3=3+2căn 2
=>2x=2 căn 2
=>x=căn 2
b: =>2 căn x-1+căn x-1=15
=>3 căn x-1=15
=>x-1=25
=>x=26
c: =>|x-4|=2x+7
TH1: x>=4
=>2x+7=x-4
=>x=-11(loại)
TH2: x<4
=>2x+7=4-x
=>3x=-3
=>x=-1(nhận)

\(a,\Leftrightarrow\Delta'=\left(m-1\right)^2-\left(m-2\right)\ge0\\ \Leftrightarrow m^2-3m+3\ge0\\ \Leftrightarrow\left(m-\dfrac{3}{2}\right)^2+\dfrac{3}{4}\ge0\left(\text{luôn đúng}\right)\)
Vậy PT có 2 nghiệm pb với mọi m
\(b,\Leftrightarrow0< x_1< x_2\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\left(m-1\right)>0\\m-2>0\end{matrix}\right.\Leftrightarrow m>2\\ c,\text{Thay }x=2\Leftrightarrow4-4\left(m-1\right)+m-2=0\\ \Leftrightarrow m=2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\\ d,\text{Viét: }\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m-2\end{matrix}\right.\\ x_1^2+x_2^2=8\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=8\\ \Leftrightarrow4\left(m-1\right)^2-2\left(m-2\right)=8\\ \Leftrightarrow4m^2-10m=0\\ \Leftrightarrow m\left(2m-5\right)=0\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{5}{2}\end{matrix}\right.\)

Độ dài quãng đường BD:
\(BD=\dfrac{CD}{sin\widehat{CBD}}=\dfrac{10}{sin3^050'}\approx150\left(m\right)=0,15\left(km\right)\)
Thời gian đi hết đoạn AB:
\(t_1=\dfrac{0,4}{4}=0,1\left(h\right)\)
Thời gian đi hết đoạn BD:
\(t_2=\dfrac{0,15}{3}=0,05\left(h\right)\)
Tổng thời gian:
\(t=t_1+t_2=0,15\left(h\right)=9\left(ph\right)\)
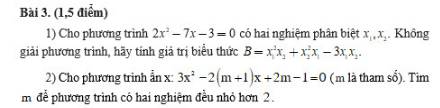






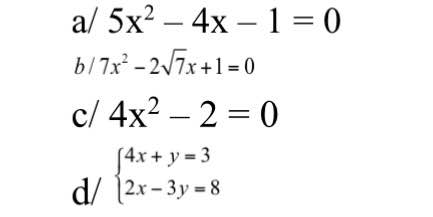


1.
Áp dụng định lý Viet:
$x_1+x_2=\frac{7}{2}$
$x_1x_2=\frac{-3}{2}$
Khi đó:
$B=x_1^2x_2+x_2^2x_1-3x_1x_2=x_1x_2(x_1+x_2)-3x_1x_2$
$=\frac{-3}{2}.\frac{7}{2}-3.\frac{-3}{2}=\frac{-3}{4}$
2.
Để pt có 2 nghiệm $x_1,x_2$ thì:
$\Delta'=(m+1)^2-3(2m-1)\geq 0$
$\Leftrightarrow m^2-4m+4\geq 0$
$\Leftrightarrow (m-2)^2\geq 0\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
$x_1+x_2=\frac{2(m+1)}{3}$
$x_1x_2=\frac{2m-1}{3}$
Để PT có 2 nghiệm $x_1,x_2<2$ thì:
\(\left\{\begin{matrix} x_1+x_2< 4\\ (x_1-2)(x_2-2)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_1+x_2<4\\ x_1x_2-2(x_1+x_2)+4>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{2(m+1)}{3}<4\\ \frac{2m-1}{3}-2.\frac{2(m+1)}{3}+4>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m<5\\ m< \frac{7}{2}\end{matrix}\right.\Leftrightarrow m< \frac{7}{2}\)
Vậy..........