
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 1
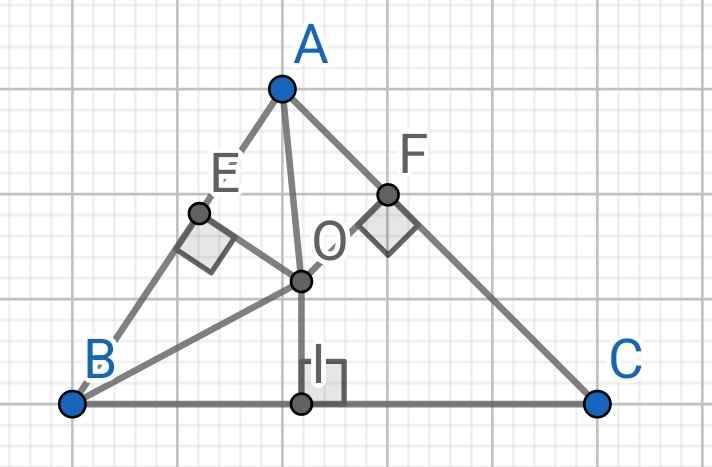 Do BO là tia phân giác của ∠ABC (gt)
Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
Bài 2
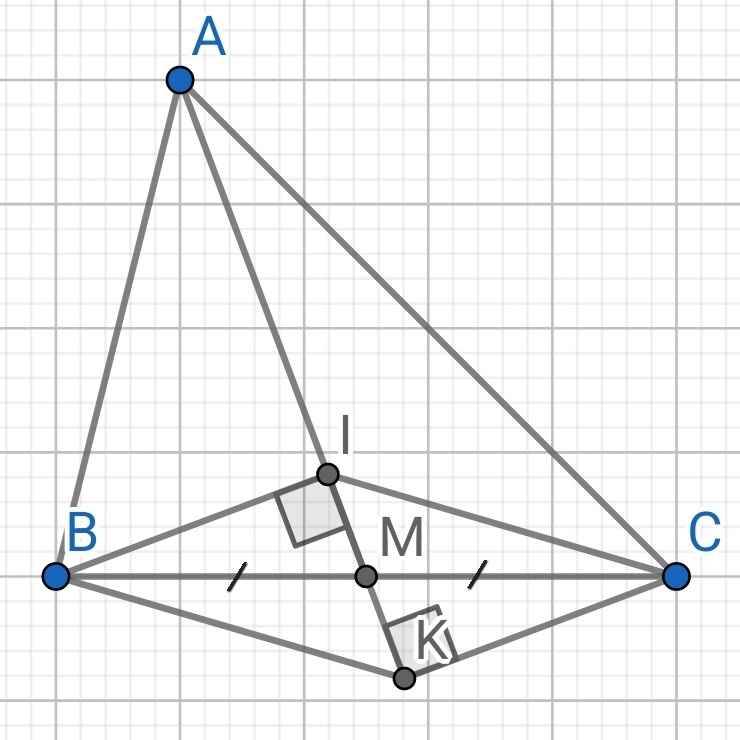 a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI


4:
a: =>2/5x+7/20-2/20=1/10
=>2/5x+5/20=1/10
=>2/5x=1/10-1/4=4/40-10/40=-6/40=-3/20
=>x=-3/20:2/5=-3/20*5/2=-15/40=-3/8
b: 3/2-1/2x=-1/3+3=8/3
=>1/2x=3/2-8/3=9/6-16/6=-7/6
=>x=-7/6*2=-7/3
c: 15/8-1/8:(1/4x-0,5)=5/4
=>1/8:(1/4x-1/2)=15/8-5/4=15/8-10/8=5/8
=>1/4x-1/2=1/8:5/8=1/5
=>1/4x=1/5+1/2=7/10
=>x=7/10*4=28/10=2,8
d: \(\Leftrightarrow\left[\left(x+\dfrac{1}{2}\right)^3-\dfrac{5}{4}\right]=\dfrac{11}{4}-\dfrac{5}{8}=\dfrac{22-5}{8}=\dfrac{17}{8}\)
=>\(\left(x+\dfrac{1}{2}\right)^3=\dfrac{17}{8}+\dfrac{5}{4}=\dfrac{27}{8}\)
=>x+1/2=3/2
=>x=1

Bài 1:
Vì $AQ\parallel BR$ nên $\widehat{PQA}=\widehat{QRB}$ (hai góc đồng vị )
$\Rightarrow \widehat{QRB}=x$
Lại có:
$Q,R,S$ thẳng hàng nên
$\widehat{QRS}=180^0$
$\widehat{QRB}+\widehat{BRC}+\widehat{CRS}=180^0$
$x+2x+75^0=180^0$
$3x+75^0=180^0$
$x=35^0$

\(-\frac{1}{7}+\frac{5}{3}+\frac{5}{4}+\frac{1}{3}-\frac{3}{2}\)
\(=\left(-\frac{1}{7}+\frac{5}{3}-\frac{3}{2}\right)+\left(\frac{5}{3}+\frac{1}{3}\right)\)
\(=\frac{-6}{42}+\frac{70}{42}-\frac{63}{42}+\frac{6}{3}\)
\(=\frac{-6+70-63}{42}+2\)
\(=\frac{1}{42}+\frac{84}{42}\)
\(=\frac{85}{42}\)

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.



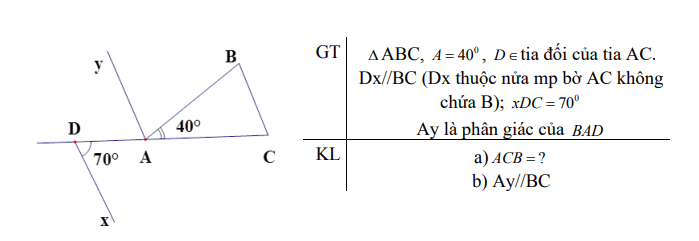
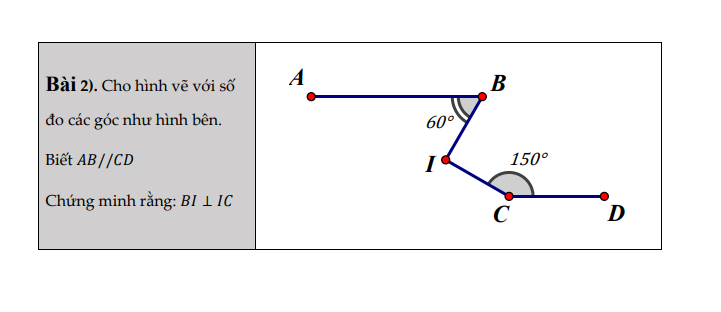


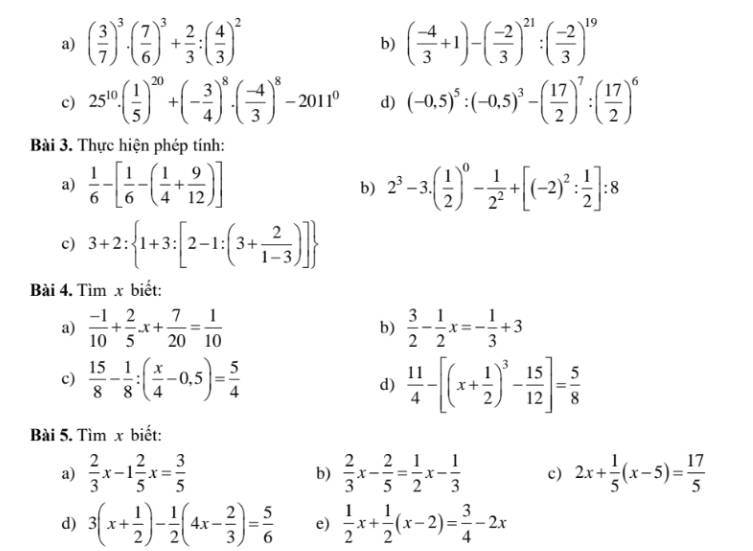

Mình không biết nha
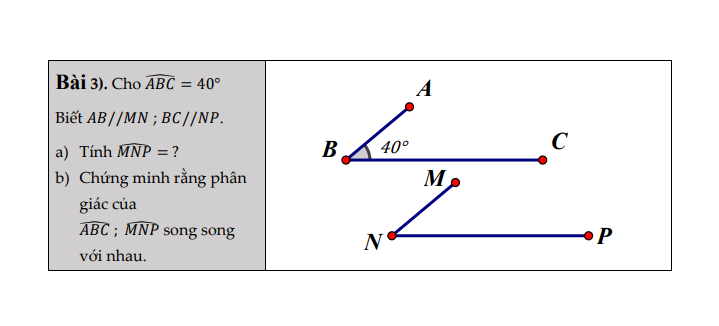
Bài 3 :
a) Kéo dài tia NM và NM cắt BC tại S
Khi đó ta có :
\(\hept{\begin{cases}\widehat{ABC}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\\\widehat{MNP}=\widehat{BSM}\left(\text{ 2 góc so le trong }\right)\end{cases}}\Rightarrow\widehat{ABC}=\widehat{MNP}\Rightarrow\widehat{MNP}=40^o\)
b) Vẽ \(\hept{\begin{cases}\text{Bx là tia phân giác của }\widehat{ABC}\\\text{Ny là tia phân giác của }\widehat{MNP}\end{cases}}\)
\(\Rightarrow\widehat{B_1}=B_2=\widehat{N_1}=\widehat{N_2}=\frac{\widehat{ABC}}{2}=\frac{\widehat{MNP}}{2}=\frac{40^o}{2}=20^o\left(\text{do }\widehat{ABC}=\widehat{MNP}\right)\)
Vẽ Sz // Bx => \(\widehat{B_2}=\widehat{S_1}\)
Lại có \(\widehat{BSN}=\widehat{MSP}\Rightarrow\frac{\widehat{BSN}}{2}=\frac{\widehat{MSP}}{2}\Rightarrow\widehat{S_2}=\widehat{N_1}\)mà \(\widehat{S_2}\text{ và }\widehat{N_1}\)là 2 góc so le trong
=> Sz // Ny mà Sz // Bx => Bx // Ny hay tia phân giác của 2 góc \(\widehat{ABC}\text{ và }\widehat{MNP}\)song song nhau