
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


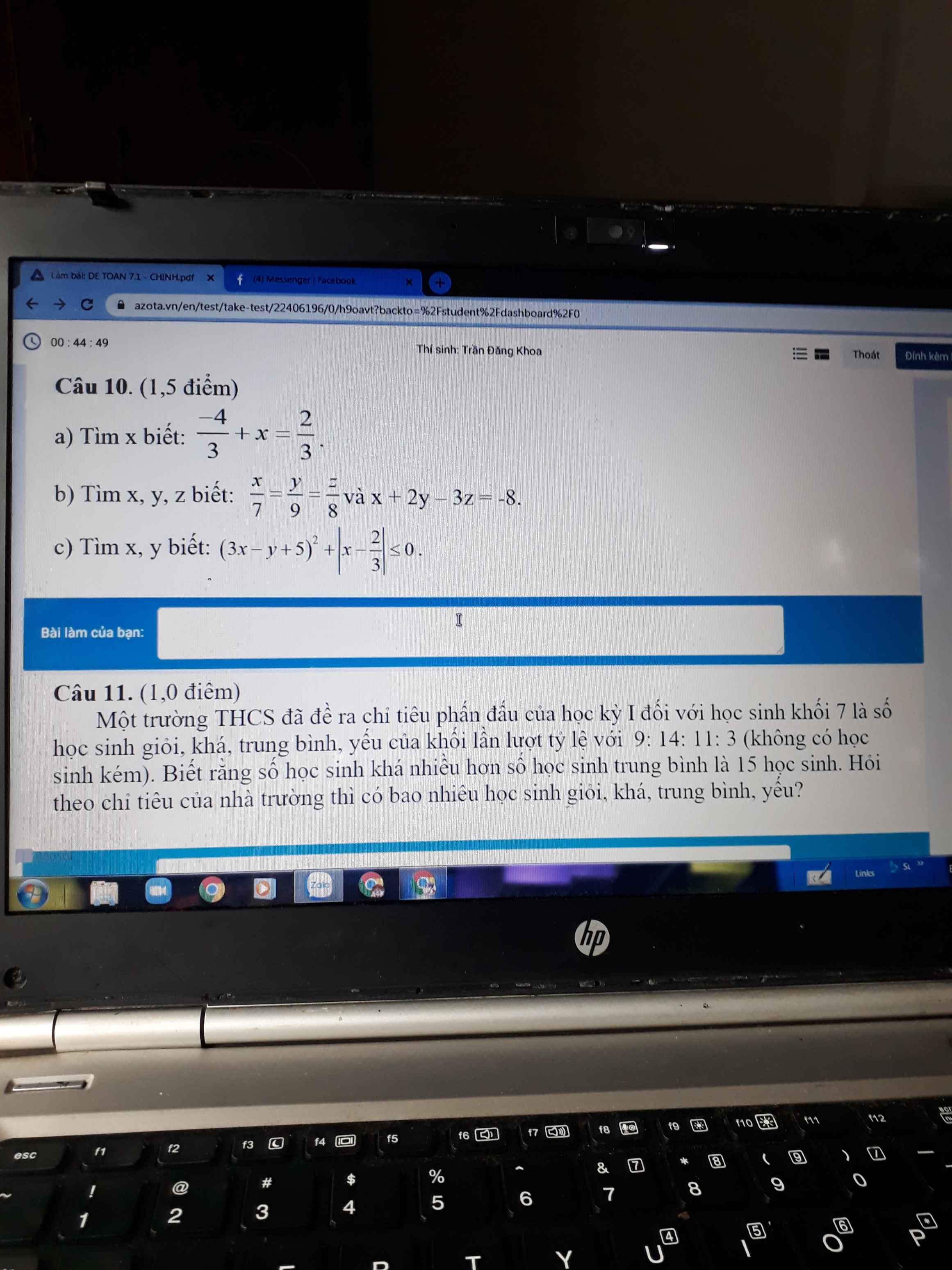
Câu 10
a) \(-\dfrac{4}{3}+x=\dfrac{2}{3}\)
\(x=\dfrac{2}{3}+\dfrac{4}{3}\)
\(x=2\)
b) \(\dfrac{x}{7}=\dfrac{y}{9}=\dfrac{z}{8}\) \(\Rightarrow\dfrac{x}{7}=\dfrac{2y}{18}=\dfrac{3z}{24}\)
và \(x+2y-3z=-8\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{7}=\dfrac{2y}{18}=\dfrac{3z}{24}=\dfrac{x+2y-3z}{7+18-24}=\dfrac{-8}{1}=-8\)
\(\dfrac{x}{7}=-8\Rightarrow x=-8.7=-56\)
\(\dfrac{y}{9}=-8\Rightarrow y=-8.9=-72\)
\(\dfrac{z}{8}=-8\Rightarrow z=-8.8=-64\)
Vậy \(x=-56;y=-72;z=-64\)
c) \(\left(3x-y+5\right)^2+\left|x-\dfrac{2}{3}\right|\le0\)
Do \(\left(3x-y+5\right)^2\ge0;\left|x-\dfrac{2}{3}\right|\ge0\)
\(\Rightarrow\left(3x-y+5\right)^2+\left|x-\dfrac{2}{3}\right|=0\)
\(\Rightarrow\left(3x-y+5\right)^2=0;\left|x-\dfrac{2}{3}\right|=0\)
*) \(\left|x-\dfrac{2}{3}\right|=0\)
\(\Rightarrow x-\dfrac{2}{3}=0\)
\(x=\dfrac{2}{3}\)
*) \(\left(3x-y+5\right)^2=0\)
\(\Rightarrow3x-y+5=0\)
\(3.\dfrac{2}{3}-y+5=0\)
\(2-y+5=0\)
\(-y+7=0\)
\(y=7\)
Vậy \(x=\dfrac{2}{3};y=7\)
Câu 11:
Gọi x (học sinh, y (học sinh), z (học sinh), t (học sinh) lần lượt là số học sinh giỏi, khá, trung bình, yếu của khối 7 theo chỉ tiêu của nhà trường
Do số học sinh giỏi, khá, trung bình, yếu lần lượt tỉ lệ với 9; 14; 11; 3 nên:
\(\dfrac{x}{9}=\dfrac{y}{14}=\dfrac{z}{11}=\dfrac{t}{3}\)
Do số học sinh khá nhiều hơn số học sinh trung bình là 15 học sinh nên:
\(y-z=15\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{9}=\dfrac{y}{14}=\dfrac{z}{11}=\dfrac{t}{3}=\dfrac{y-z}{14-11}=\dfrac{15}{3}=5\)
\(\dfrac{x}{9}=5\Rightarrow x=5.9=45\)
\(\dfrac{y}{14}=5\Rightarrow y=5.14=70\)
\(\dfrac{z}{11}=5\Rightarrow z=5.11=55\)
\(\dfrac{t}{3}=5\Rightarrow t=5.3=15\)
Vậy số học sinh giỏi, khá, trung bình, yếu của khối 7 theo chỉ tiêu của nhà trường lần lượt là: 45 học sinh; 70 học sinh; 55 học sinh; 15 học sinh
Câu 11:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{9}=\dfrac{b}{14}=\dfrac{c}{11}=\dfrac{d}{3}=\dfrac{b-c}{14-11}=5\)
Do đó: a=45; b=70; c=55; d=15

1: \(\Leftrightarrow3^x\cdot\dfrac{1}{7}\cdot3+3^x\cdot9\cdot\dfrac{1}{2}=\dfrac{23}{14}\cdot3^5\)
=>\(3^x\left(\dfrac{3}{7}+\dfrac{9}{2}\right)=\dfrac{23}{14}\cdot3^5\)
=>\(3^x\cdot\dfrac{69}{14}=\dfrac{23}{14}\cdot3^5\)
=>\(3^{x+1}\cdot\dfrac{23}{14}=\dfrac{23}{14}\cdot3^5\)
=>\(3^{x+1}=3^5\)
=>x+1=5
=>x=4
2: \(\Leftrightarrow4^x\cdot\dfrac{64}{5}+4^x\cdot\dfrac{4}{7}=4^5\cdot\dfrac{117}{35}\)
=>\(4^x\left(\dfrac{64}{5}+\dfrac{4}{7}\right)=4^5\cdot\dfrac{117}{35}\)
=>\(4^{x+1}\cdot\left(\dfrac{16}{5}+\dfrac{1}{7}\right)=4^5\cdot\dfrac{117}{35}\)
=>\(4^{x+1}=4^5\)
=>x+1=5
=>x=4
3:
\(\Leftrightarrow2^x\cdot2\cdot\dfrac{-3}{20}+2^x\cdot4=-\dfrac{148}{5}\)
=>\(2^x\cdot\left(-\dfrac{3}{10}+4\right)=-\dfrac{148}{5}\)
=>\(2^x=-8\)
=>\(x\in\varnothing\)
4: \(\Leftrightarrow5^x\cdot125+\dfrac{5}{6}\cdot5^x\cdot625=\dfrac{275}{2}\)
=>\(5^x\left(125+625\cdot\dfrac{5}{6}\right)=\dfrac{275}{2}\)
=>\(5^x=\dfrac{33}{155}\)
=>\(x\in\varnothing\)

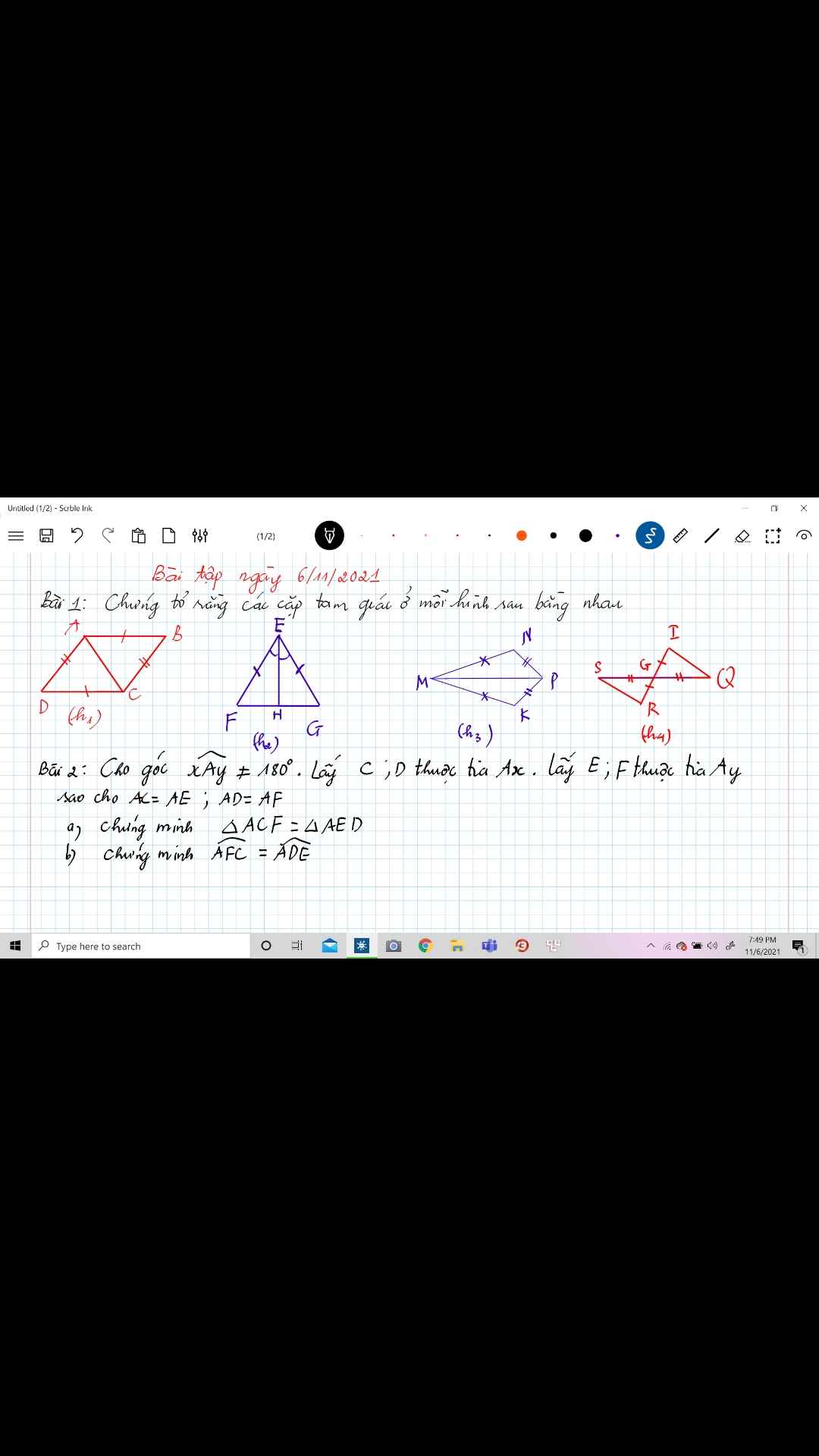
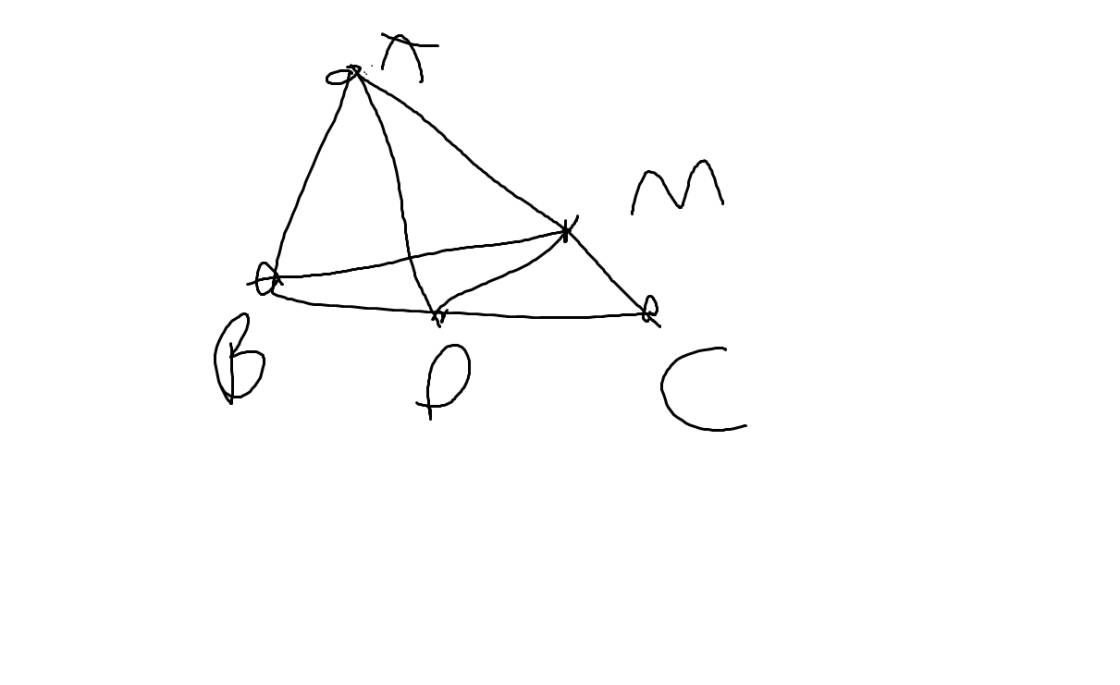
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.

Bài 1:
a: Ta có: \(3\left(x-\dfrac{1}{2}\right)-3\left(x-\dfrac{1}{3}\right)=x\)
\(\Leftrightarrow x=3x-\dfrac{3}{2}-3x+1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\)
b: Ta có: \(-\dfrac{4}{3}\left(x-\dfrac{1}{4}\right)=\dfrac{3}{2}\left(2x-1\right)\)
\(\Leftrightarrow x\cdot\dfrac{-4}{3}+\dfrac{1}{3}-3x+\dfrac{3}{2}=0\)
\(\Leftrightarrow x\cdot\dfrac{-13}{3}=-\dfrac{11}{6}\)
hay \(x=\dfrac{11}{26}\)

Câu 4:
Số đo các góc còn lại là \(47^0;133^0;133^0\)

a: Xét ΔACF và ΔAED có
AC=AE
\(\widehat{A}\) chung
AF=AD
Do đó: ΔACF=ΔAED
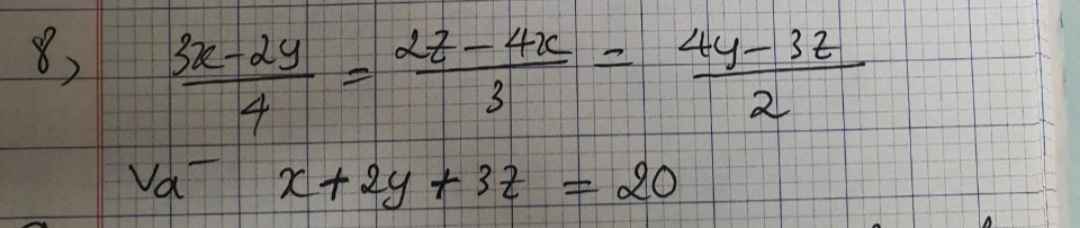

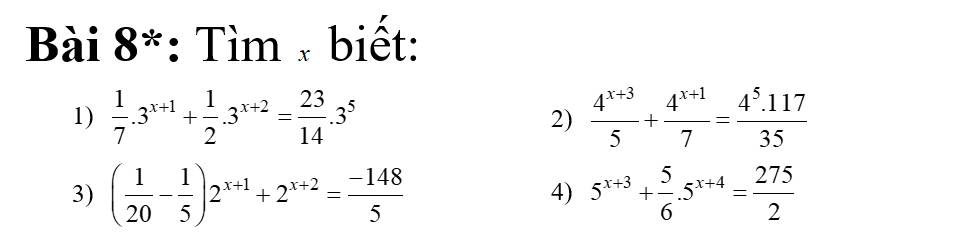


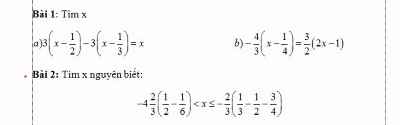 giúp mik giải 2 bài này vs ạ
giúp mik giải 2 bài này vs ạ

Lời giải:
Áp dụng TCDTSBN:
$\frac{3x-2y}{4}=\frac{2z-4x}{3}=\frac{4y-3z}{2}$
$=\frac{4(3x-2y)}{16}=\frac{3(2z-4x)}{9}=\frac{2(4y-3z)}{4}$
$=\frac{4(3x-2y)+3(2z-4x)+2(4y-3z)}{16+9+4}=\frac{0}{29}=0$
$\Rightarrow 3x-2y=2z-4x=4y-3z=0$
$\Rightarrow 3x=2y; 2z=4x$
$\Rightarrow \frac{x}{2}=\frac{y}{3}; \frac{x}{2}=\frac{z}{4}$
$\Rightarrow \frac{x}{2}=\frac{y}{3}=\frac{z}{4}$
Đặt $\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=t$
$\Rightarrow x=2t; y=3t; z=4t$. Khi đó:
$x+2y+3z=20$
$\Rightarrow 2t+2.3t+3.4t=20$
$\Rightarrow 2t+6t+12t=20$
$\Rightarrow 20t=20\Rightarrow t=1$
Do đó:
$x=2t=2; y=3t=3; z=4t=4$