
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ phương trình d ta thấy d có 1 vtpt là \(\left(-1;4\right)\)
a.
Do \(d_1\perp d\Rightarrow d_1\) nhận \(\left(4;1\right)\) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-2\right)+1\left(y+3\right)=0\Leftrightarrow4x+y-3=0\)
b.
Do \(d_2||d\) nên \(d_2\) nhận \(\left(-1;4\right)\) là 1 vtpt
Phương trình \(d_2\):
\(-1\left(x-2\right)+4\left(y+3\right)=0\Leftrightarrow-x+4y+14=0\)
c.
\(d\left(E;d\right)=\dfrac{\left|-2+4.\left(-3\right)-1\right|}{\sqrt{\left(-1\right)^2+4^2}}=\dfrac{15\sqrt{17}}{17}\)

Câu 2:
\(a,\Leftrightarrow\Delta'=\left(1-m\right)^2-\left(m^2-m\right)>0\\ \Leftrightarrow m^2-2m+1-m^2+m>0\\ \Leftrightarrow1-m>0\Leftrightarrow m< 1\\ b,\text{Áp dụng Viét: }\left\{{}\begin{matrix}x_1+x_2=2\left(1-m\right)\\x_1x_2=m^2-m\end{matrix}\right.\\ \left(2x_1-1\right)\left(2x_2-1\right)-x_1x_2=1\\ \Leftrightarrow2x_1x_2-2\left(x_1+x_2\right)+1-x_1x_2=1\\ \Leftrightarrow x_1x_2-2\left(x_1+x_2\right)=0\\ \Leftrightarrow m^2-m-4\left(1-m\right)=0\\ \Leftrightarrow m^2+3m-4=0\\ \Leftrightarrow\left(m-1\right)\left(m+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-4\left(tm\right)\end{matrix}\right.\)
Vậy m=-4
Câu 1:
\(1,\Leftrightarrow2x-2=3\Leftrightarrow x=\dfrac{5}{2}\\ 2,ĐK:x\ne\pm1\\ PT\Leftrightarrow\dfrac{2x^2+2x-1}{x^2-1}=2\\ \Leftrightarrow2x^2+2x-1=2x^2-2\\ \Leftrightarrow2x=-1\Leftrightarrow x=-\dfrac{1}{2}\left(tm\right)\\ 3,\Leftrightarrow\left[{}\begin{matrix}3x-2=2x-1\\3x-2=1-2x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)
\(4,\Leftrightarrow\left[{}\begin{matrix}3x-1=2-x\left(x\ge\dfrac{1}{3}\right)\\3x-1=x-2\left(x< \dfrac{1}{3}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\left(tm\right)\\x=-\dfrac{1}{2}\left(tm\right)\end{matrix}\right.\\ 5,\Leftrightarrow4x^2-2x+10=9x^2-6x+1\left(x\le\dfrac{1}{3}\right)\\ \Leftrightarrow5x^2-4x-9=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{9}{5}\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
\(6,\Leftrightarrow3x^2-9x+1=x^2-4x+4\left(x\ge2\right)\\ \Leftrightarrow2x^2-5x-3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\\ 7,\Leftrightarrow2x^2+3x-4=7x+2\left(x\ge-\dfrac{2}{7}\right)\\ \Leftrightarrow x^2-2x-3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-1\left(ktm\right)\end{matrix}\right.\)


`2)`
`@` Xét `3x+6 >= 0<=>x >= -2`
`=>A=[-2;+oo)`
`@` Xét `|x-2| < 3`
`<=>-3 < x-2 < 3`
`<=>-1 < x < 5=>B=(-1;5)`
Có: `A nn B=(-1;5)`
`A uu B=[-2;+oo)`
`R \\ B=(-oo;-1]uu[5;+oo)`
_______
`3)`
`@` Xét `x+3 >= 2x+7<=>x <= -4=>A=(-oo;-4]`
`@` Xét `4x+5 > 0<=>x > -5/4=>B=(-5/4;+oo)`
`@` Xét `|x+4| < 2<=>-2 < x+4 < 2<=>-6 < x < -2 =>C=(-6;-2)`
Có: `A nn B nn C=\emptyset`
`A \\ B nn C=(-6;-4]`
`C \\ A nn B=\emptyset`.

Bài 4:
Theo định lý sin ta có:
\(\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
\(\Rightarrow BC=a=\dfrac{b\cdot sinA}{sinB}=\dfrac{2\cdot sin60^o}{sin45^o}=\sqrt{6}\)
\(\Rightarrow\widehat{C}=180^o-60^o-45^o=75^o\)
\(\dfrac{AC}{sinB}=\dfrac{AB}{sinC}\)
\(\Rightarrow AB=c=\dfrac{b\cdot sinC}{sinB}=\dfrac{2\cdot sin75^o}{sin45^o}=1+\sqrt{3}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AC\cdot AB\cdot sinA=\dfrac{1}{2}\cdot2\cdot\left(1+\sqrt{3}\right)\cdot sin75^o=\dfrac{\sqrt{6}+2\sqrt{2}}{2}\) (đvdt)
Bán kình hình tròn tam giác ABC khi đó là:
\(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{2\cdot\left(1+\sqrt{3}\right)\cdot\sqrt{6}}{4\cdot\left(\dfrac{\sqrt{6}+2\sqrt{2}}{2}\right)}=3-\sqrt{3}\)
Bài 3:
a) Xét tam giác ABC theo định lý côsin ta có:
\(cosC=\dfrac{a^2+b^2-c^2}{2ab}=\dfrac{8^2+10^2-13^2}{2\cdot8\cdot10}=-0,03125\)
\(\Rightarrow\widehat{C}=cos^{-1}-0,03125\approx91^o>90^o\)
Nên tam giác ABC có góc C là góc tù
c) Theo hệ thức Heron ta có diện tích tam giác ABC là:
\(S_{ABC}=\sqrt{p\cdot\left(p-a\right)\cdot\left(p-b\right)\cdot\left(p-c\right)}\)
\(\Rightarrow S_{ABC}=\sqrt{\dfrac{8+10+13}{2}\cdot\left(\dfrac{8+10+13}{2}-8\right)\cdot\left(\dfrac{8+10+13}{2}-10\right)\cdot\left(\dfrac{8+10+13}{2}-13\right)}\)
\(\Rightarrow S_{ABC}\approx40\) (đvdt)
b) Bán kính đường tròn ngoại tiếp tam giác ABC là:
\(S_{ABC}=\dfrac{abc}{4R}\)
\(\Rightarrow R=\dfrac{abc}{4S_{ABC}}=\dfrac{8\cdot10\cdot13}{4\cdot40}=6,5\)

Câu 1:
\(\left(4x+3\right)\left(3x^2+x-2\right)\left(2x^2-3x-5\right)=0\\ \Leftrightarrow\left(4x+3\right)\left(3x-2\right)\left(x+1\right)\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{4}\\x=-1\\x=\dfrac{2}{3}\\x=\dfrac{5}{2}\end{matrix}\right.\\ \Leftrightarrow A=\left\{-1;-\dfrac{3}{4};\dfrac{2}{3};\dfrac{5}{2}\right\}\)
Câu 2:
\(\left(x^2-4\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\\x=3\end{matrix}\right.\Leftrightarrow A=\left\{-2;2;3\right\}\\ \left|5x\right|-11\le0\Leftrightarrow\left|5x\right|\le11\Leftrightarrow-11\le5x\le11\\ \Leftrightarrow-\dfrac{11}{5}\le x\le\dfrac{11}{5}\\ \Leftrightarrow B=\left[-\dfrac{11}{5};\dfrac{11}{5}\right]\)
\(\Leftrightarrow A\cap B=\left\{-2;2\right\}\\ A\cup B=\left[-\dfrac{11}{5};3\right]\\ A\B=\left\{3\right\}\)

a) \(d\left(A;\Delta\right)=\dfrac{\left|4.1-3.3+2\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{3}{5}\)
b) \(\overrightarrow{AB}=\left(-3;-2\right)\) là VTCP của đường thẳng d
PT tham số của d: \(\left\{{}\begin{matrix}x=1-3t\\y=3-2t\end{matrix}\right.\left(t\in R\right)\)
c) Đường tròn (C) có bán kính \(R=AB=\sqrt{\left(1+2\right)^2+\left(3-1\right)^2}=\sqrt{13}\)
PT đường tròn (C): \(\left(x-1\right)^2+\left(y-3\right)^2=13\)






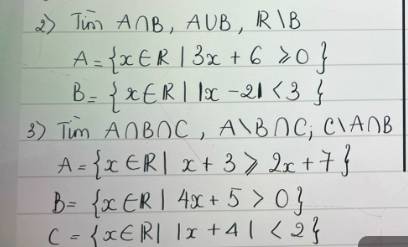



Bài 5:
a: \(x^2+y^2-2x+4y-20=0\)
=>x^2-2x+1+y^2+4y+4=25
=>(x-1)^2+(y+2)^2=25
Khi x=4 và y=2 thì ta có: (4-1)^2+(2+2)^2=3^2+4^2=25
=>M thuộc (C)
b: Tâm là I(1;-2); R=5; M(4;2)
vecto IM=(3;4)
=>(d) có VTPT là (3;4)
Phương trình tiếp tuyến tại M của (C) là:
3(x-4)+4(y-2)=0
=>3x+4y-20=0