
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi thời gian của T,D,M lần lượt là \(a,b,c(giờ;a,b,c>0)\)
Áp dụng tc dtsbn:
\(10a=9b=8c\Leftrightarrow\dfrac{10a}{360}=\dfrac{9b}{360}=\dfrac{8c}{360}\Leftrightarrow\dfrac{a}{36}=\dfrac{b}{40}=\dfrac{c}{45}=\dfrac{c-a}{45-36}=\dfrac{0,3}{9}=\dfrac{1}{30}\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{6}{5}\\b=\dfrac{4}{3}\\c=\dfrac{3}{2}\end{matrix}\right.\)
Vậy ...

\(\text{Bài 1:a)}25\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)-35\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\dfrac{478}{19}.\left(-\dfrac{4}{5}\right)-\dfrac{668}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{478}{19}-\dfrac{668}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{-190}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(-10\right)=8\)
\(\text{b)}5:\left(-\dfrac{5}{2}\right)^2+\dfrac{2}{15}.\sqrt{\dfrac{9}{4}}-\left(-2021\right)^0+0,25\)
\(=5:\dfrac{25}{4}+\dfrac{2}{15}.\dfrac{3}{2}-1+\dfrac{1}{4}\)
\(=\dfrac{4}{5}+\dfrac{1}{5}-1+\dfrac{1}{4}\)
\(=1-1+\dfrac{1}{4}\)
\(=0+\dfrac{1}{4}=\dfrac{1}{4}\)
\(\text{Bài 2:a)}\dfrac{8}{5}-\dfrac{3}{5}:x=0,4\)
\(\dfrac{3}{5}:x=\dfrac{8}{5}-0,4=\dfrac{6}{5}\)
\(x=\dfrac{3}{5}.\dfrac{5}{6}=\dfrac{1}{2}\)
\(\text{b)}\left(3x-\dfrac{1}{2}\right)^2+\dfrac{21}{25}=1\)
\(\left(3x-\dfrac{1}{2}\right)^2\) \(=1-\dfrac{21}{25}=\dfrac{4}{25}=\pm\left(\dfrac{2}{5}\right)^2\)
\(\text{Vậy }3x-\dfrac{1}{2}=\dfrac{2}{5}\)
\(3x\) \(=\dfrac{2}{5}+\dfrac{1}{2}=\dfrac{9}{10}\)
\(x\) \(=\dfrac{9}{10}.\dfrac{1}{3}=\dfrac{3}{10}\)
\(\text{hoặc }3x-\dfrac{1}{2}=\dfrac{-2}{5}\)
\(3x\) \(=\left(\dfrac{-2}{5}\right)+\dfrac{1}{2}=\dfrac{1}{10}\)
\(x\) \(=\dfrac{1}{10}.\dfrac{1}{3}=\dfrac{1}{30}\)
\(\Rightarrow x\in\left\{\dfrac{3}{10};\dfrac{1}{30}\right\}\)
Bài 2:
a: =>3/5:x=6/5
hay x=3/5:6/5=1/2
b: \(\Leftrightarrow\left(3x-\dfrac{1}{2}\right)^2=\dfrac{4}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{1}{2}=\dfrac{2}{5}\\3x-\dfrac{1}{2}=-\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{10}\\x=\dfrac{1}{30}\end{matrix}\right.\)

Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$

\(a,\Leftrightarrow m-2=3\Leftrightarrow m=5\\ b,y=f\left(x\right)=\left(5-2\right)x=3x\\ \Leftrightarrow f\left(3\right)+\dfrac{1}{3}f\left(-2\right)=9+\dfrac{1}{3}\cdot\left(-6\right)=7\)

Bài 4:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=CD

a) Om là tia phân giác \(\widehat{xOz}\left(gt\right)\)
\(\Rightarrow\widehat{mOz}=\dfrac{1}{2}\widehat{xOz}\)
\(\Rightarrow2\widehat{mOz}=\widehat{xOz}\)
CM tương tự, ta được: \(2\widehat{nOz}=\widehat{yOz}\)
Ta có: \(\widehat{xOz}+\widehat{yOz}=180^o\)(2 góc bù nhau)
\(\Rightarrow2\widehat{mOz}+2\widehat{nOz}=180^o\)
\(\Rightarrow\widehat{mOz}+\widehat{nOz}=90^o\)
\(\Rightarrow\widehat{mOn}=90^o\)
\(\Rightarrow Om\perp On\)
b) Đề của bạn mình thấy nó sai ở chỗ \(Om\perp Az\) vì nhìn hình là thấy không vuông nên mình xin sửa đề thành \(Om\perp At\).
Vì \(Om\perp ON\) (c/m phần a) và At//On:
\(\Rightarrow Om\perp At\) (quan hệ giữa vuông góc và song song)

 mn giúp mik vs mik cần gấp( có trình bày nha~)
mn giúp mik vs mik cần gấp( có trình bày nha~)

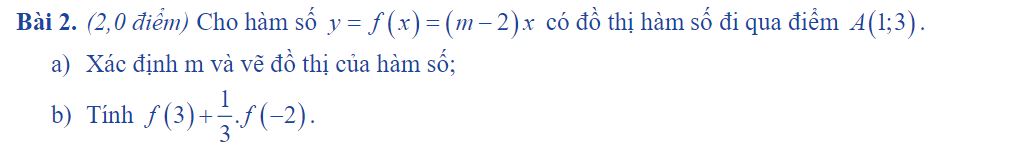 mn giúp mik vs mik cần gấp( có trình bày đồ thị nha)
mn giúp mik vs mik cần gấp( có trình bày đồ thị nha)
