
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow x=0\Leftrightarrow\left\{{}\begin{matrix}5-m=y\\3+m=y\end{matrix}\right.\Leftrightarrow y=4\Leftrightarrow5-m=4\Leftrightarrow m=1\)


Áp dụng BĐT AM-GM ta có:
\(\left(a+1\right)^2+b^2+1=a^2+2a+1+b^2+1=\left(a^2+b^2\right)+2a+2\ge2\left(ab+a+1\right)\)
\(\Rightarrow\frac{1}{\left(a+1\right)^2+b^2+1}\le\frac{1}{2\left(ab+a+1\right)}\)(1)
\(\left(b+1\right)^2+c^2+1=b^2+2b+1+c^2+1=\left(b^2+c^2\right)+2b+2\ge2\left(bc+b+1\right)\)
\(\Rightarrow\frac{1}{\left(b+1\right)^2+c^2+1}\le\frac{1}{2\left(bc+b+1\right)}\)(2)
\(\left(c+1\right)^2+a^2+1=c^2+2c+1+a^2+1=\left(c^2+a^2\right)+2c+2\ge2\left(ca+c+1\right)\)
\(\Rightarrow\frac{1}{\left(c+1\right)^2+a^2+1}\le\frac{1}{2\left(ca+c+1\right)}\)(3)
Cộng vế theo vế của (1) ; (2) ; (3) ta được:
\(\frac{1}{\left(a+1\right)^2+b^2+1}+\frac{1}{\left(b+1\right)^2+c^2+1}+\frac{1}{\left(c+1\right)^2+a^2+1}\le\frac{1}{2}\left(\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{ca+c+1}\right)=\frac{1}{2}\)Dấu "=" xảy ra \(\Leftrightarrow a=b=b=1\)

\(A=\frac{x}{\sqrt{x}-1}+\frac{\sqrt{x}-2x}{x-\sqrt{x}}\)
\(=\frac{x}{\sqrt{x}-1}+\frac{1-2\sqrt{x}}{\sqrt{x}-1}=\frac{x-2\sqrt{x}+1}{\sqrt{x}-1}=\frac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}=\sqrt{x}-1\)




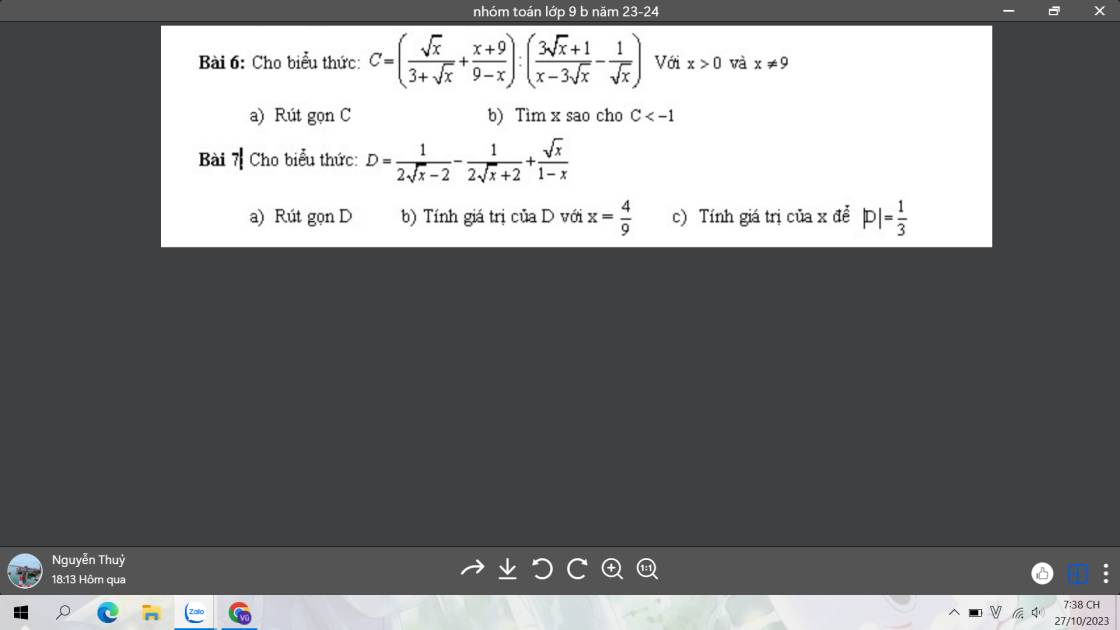
7:
a: ĐKXĐ: x>=0; x<>1
\(D=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\)
\(=\dfrac{1}{2\left(\sqrt{x}-1\right)}-\dfrac{1}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)
b: Khi x=4/9 thì \(D=\dfrac{-1}{\dfrac{2}{3}+1}=-1:\dfrac{5}{3}=-\dfrac{3}{5}\)
c: |D|=1/3
=>D=-1/3 hoặc D=1/3
=>\(\left[{}\begin{matrix}\dfrac{-1}{\sqrt{x}+1}=\dfrac{-1}{3}\\\dfrac{-1}{\sqrt{x}+1}=\dfrac{1}{3}\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}+1=3\)
=>\(\sqrt{x}=2\)
=>x=4
6:
a: \(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}-x+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\)
\(=\dfrac{3\left(\sqrt{x}+3\right)}{3+\sqrt{x}}\cdot\dfrac{-\sqrt{x}}{2\sqrt{x}+4}=\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
b: C<-1
=>C+1<0
=>\(\dfrac{-3\sqrt{x}+2\sqrt{x}+4}{2\sqrt{x}+4}< 0\)
=>\(-\sqrt{x}+4< 0\)
=>\(-\sqrt{x}< -4\)
=>\(\sqrt{x}>4\)
=>x>16
\(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\\ =\dfrac{3\sqrt{x}-x+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{3\left(\sqrt{x}+3\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
Để `C < -1` Ta có :
\(\dfrac{-3}{2\sqrt{x}+4}< -1\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+1< 0\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+\dfrac{2\sqrt{x}+4}{2\sqrt{x}+4}< 0\\ \Leftrightarrow-3+2\sqrt{x}+4< 0\\ \Leftrightarrow2\sqrt{x}+1< 0\\ \Leftrightarrow2\sqrt{x}< -1\\ \Leftrightarrow\sqrt{x}< -\dfrac{1}{2}\\ \Leftrightarrow x< \dfrac{1}{4}\)







 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 

 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp

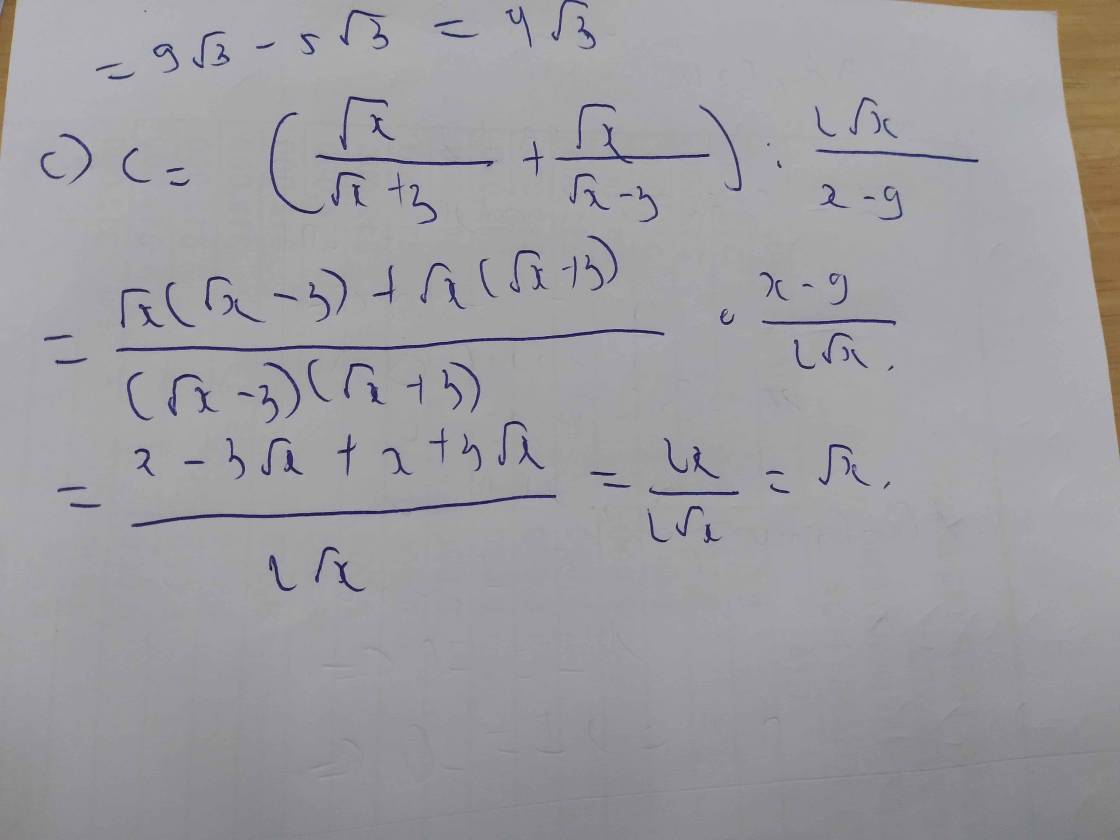
a) \(B=\left(\frac{1}{a-\sqrt{a}}+\frac{1}{\sqrt{a}-1}\right):\frac{a-1}{a-2\sqrt{a}+1}\)
\(B=\left[\frac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\frac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right].\frac{a-2\sqrt{a}+1}{a-1}\)
\(B=\frac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\frac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(B=\frac{1}{\sqrt{a}}\)
b) Khi \(a=3-2\sqrt{2}\)thì \(B=\frac{1}{\sqrt{3-2\sqrt{2}}}\)\(=\frac{1}{\sqrt{2-2\sqrt{2}+1}}\)\(=\frac{1}{\sqrt{\left(\sqrt{2}-1\right)^2}}\)\(=\frac{1}{\sqrt{2}-1}\)\(=\sqrt{2}+1\)
khó thế hok trường tiểu học mà giao bài khó thế mình lớp 4 chư bt lm