a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

=>AD=ED

b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có

BE=BA

góc EBF chung

=>ΔBEF=ΔBAC

=>BF=BC

2BF=BF+BC>FC

Bài 9:

a: Xét ΔABC có DE//BC

nên AD/AB=AE/AC

mà AB=AC

nên AD=AE

hay ΔADE cân tại A

b: Xét ΔDBC và ΔECB có 

DB=EC

\(\widehat{DBC}=\widehat{ECB}\)

BC chung

Do đó: ΔDBC=ΔECB

Suy ra: \(\widehat{OCB}=\widehat{OBC}\)

hay ΔOBC cân tại O

Bài 10 với vẽ hình cho mik với :<<

Câu 3: 

a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)

b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)

nên BC<AC=AB

c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có

BC chung

\(\widehat{EBC}=\widehat{DCB}\)

Do đó:ΔEBC=ΔDCB

d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)

nên ΔOBC cân tại O

Câu 2

a) Thay y = -2 vào biểu thức đã cho ta được:

2.(-2) + 3 = -1

Vậy giá trị của biểu thức đã cho tại y = -2 là -1

b) Thay x = -5 vào biểu thức đã cho ta được:

2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40

Vậy giá trị của biểu thức đã cho tại x = -5 là 40

Xét ΔABM và ΔDEN có 

AB=DE

\(\widehat{B}=\widehat{E}\)

BM=EN

Do đó: ΔABM=ΔDEN

Suy ra: AM=DN

Ta có:

ΔABC=ΔDEF(gt)ΔABC=ΔDEF(gt)

⇒⎧⎪⎨⎪⎩AB=DEˆABC=ˆABM=ˆDEF=ˆDENBC=EF⇒{AB=DEABC^=ABM^=DEF^=DEN^BC=EF

Ta lại có:

⎧⎪ ⎪⎨⎪ ⎪⎩BM=MC=12BC(gt)EN=NF=12EF(gt){BM=MC=12BC(gt)EN=NF=12EF(gt)

⇒BM=MC=EN=NF⇒BM=MC=EN=NF

Xét ΔABMΔABM và ΔDENΔDEN có: 

AB=DE(ΔABC=ΔDEF)AB=DE(ΔABC=ΔDEF)

ˆABM=ˆDEN(cmt)ABM^=DEN^(cmt)

BM=EN(cmt)BM=EN(cmt)

Do đó ΔABM=ΔDEN(c.g.c)ΔABM=ΔDEN(c.g.c)

⇒AM=DN (Hai cạnh tương ứng)
sr bạn mình ko bk vẽ hình trên đây

a: BC=5cm

b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có

BD chung

\(\widehat{ABD}=\widehat{EBD}\)

Do đó: ΔABD=ΔEBD

c: Ta có: ΔABD=ΔEBD

nên DA=DE

mà DE<DC

nên DA<DC

a: BC=căn 6^2+8^2=10cm

b: Xét ΔBAI vuông tại A và ΔBHI vuông tại H có

BI chung

góc ABI=góc HBI

=>ΔBAI=ΔBHI

=>IA=IH

mà IH<IC

nên IA<IC

c: Xét ΔIAK vuông tại A và ΔIHC vuông tại H có

IA=IH

góc AIK=góc HIC

=>ΔIAK=ΔIHC

=>AK=HC

d: Xét ΔBKC có BA/AK=BH/HC

nên AH//KC

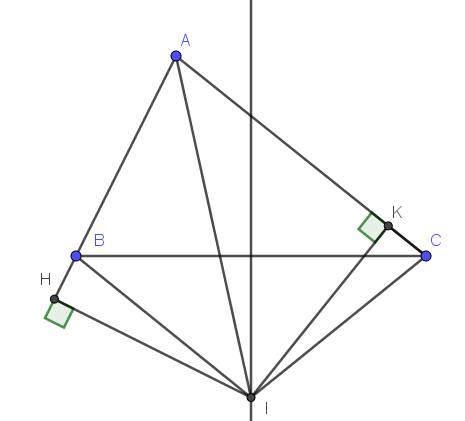
Lời giải:

Vì $I$ nằm trên đường trung trực của $BC$ nên $BI=CI$
Vì $I$ nằm trên đường phân giác $\widehat{BAC}$ nên khoảng cách từ $I$ đến $AB$ bằng khoảng cách từ $I$ đến $AC$

$\Rightarrow IH=IK$

Xét tam giác vuông $IHB$ và $IKC$ có:

$IH=IK$ (cmt)

$IB=IC$ (cmt) 

$\Rightarrow \triangle IHB=\triangle IKC$ (ch-gn) 

$\Rightarrow HB=KC$ (đpcm)

Hình vẽ:

a: \(\widehat{ACB}=90^0-60^0=30^0\)

b: Xét ΔABH và ΔKBH có 

BA=BK

BH chung

AH=KH

Do đó: ΔABH=ΔKBH

Ta có: ΔABK cân tại B

mà BI là đường trung tuyến

nên BI là đường cao