Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 23:
a)
Ta thấy $FG\perp ED\Rightarrow \widehat{GFE}=90^0$
Xét tam giác $EFG$ và $ECG$ có:
$\widehat{GFE}=\widehat{GCE}(=90^0)$
$GE$ chung
$EF=EC$ (giả thiết)
$\Rightarrow \triangle EFG=\triangle ECG$ (ch-cgv)
$\Rightarrow \widehat{FEG}=\widehat{CEG}$
$\Rightarrow EG$ là phân giác góc $\widehat{CED}$ (đpcm)
b)
Từ hai tam giác bằng nhau phần a suy ra $GF=GC(1)$
Xét tam giác $DFG$ vuông tại $F$ thì $DG> GF(2)$ do $DG là cạnh huyền.
Từ $(1);(2)\Rightarrow GC< DG$
Câu 22:
Thay giá trị $x=-1; y=2$ vào biểu thức thôi:
$P=x^2-xy+y^2=(-1)^2-(-1).2+2^2=1+2+4=7$

\(\dfrac{x-1}{3}=\dfrac{2-x}{-2}\)
⇔ \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
⇔ \(3x-6-2x+2=0\)
⇔ \(x-4=0\)
⇒ \(x=4\)

abcd chia hết cho ab*cd
=> abcd chia hết cho ab => cd chia hết cho ab
Đặt cd=k*ab (k thuộc N; 0<k<10) (*)
=> 100*ab+k*ab chia hết cho k*ab*ab
=> 100+k chia hết cho k*ab (1)
=> 100+k chia hết cho k
=> 100 chia hết cho k
=> k thuộc {1;2;4;5}
Nếu k=1 thì thay vào (1) ta có 101 chia hết cho ab (vô lí vì 101 là số nguyên tố)
Nếu k=2 thì 102 chia hết cho 2*ab
=> 51 chia hết cho ab
=> ab=51 hoặc ab=17
=> Thay vào (*) ta có cd=...
Bạn tự làm nha

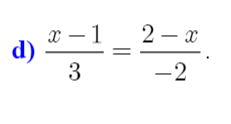

giúp mik đi cần gấp lắm rồi